人教版六年级上册4 扇形优秀复习练习题

第五单元圆

5.4 扇形

【基础巩固】

一、选择题

1．下面各圆中的涂色部分，（   ）是扇形。

A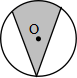． B． C．

2．如图中涂色部分的面积和半圆的面积相比，（   ）。

A．涂色部分的面积大 B．半圆的面积大 C．涂色部分的面积和半圆的面积相等

3．如图，在钟面上分针从12点整起，走15分钟经过的部分可以看作（   ）。

A．圆形 B．扇形 C．三角形 D．梯形

4．在同一个圆中，扇形的大小与这个扇形的（   ）有关。

A．圆心角 B．半径 C．直径

5．如果两个扇形的半径之比为1∶2，圆心角之比也为1∶2，那么它们的面积之比为（   ）。

A．1∶2 B．1∶4 C．1∶1 D．1∶8

二、填空题

6．如图，这是一个(        )，已知它的周长是28.56dm，它的弧长（）是(        )dm，面积是(        )dm2。（π取3.14）

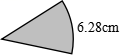
7．把一张圆形纸片对折三次（如图），此时圆心角是(        )。量得弧长是6.28cm，这张圆形纸片的直径是(        )cm。

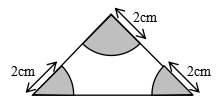
8．图中阴影部分的面积之和是(        )cm2。

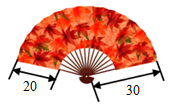
9．如图，一把折扇的骨架长是30厘米，扇面宽为20厘米，完全展开时圆心角为135°，扇面的面积为______平方厘米。

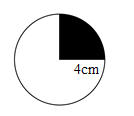
10．如图，一个圆的半径是4cm，它的直径是(        )cm，周长是(        )cm，面积是(        )cm2。在这个圆中有一个圆心角为90°的扇形，这个扇形的面积是(        )cm2。

三、作图题

11．画一个半径2厘米的圆，并用字母标出圆的半径和直径；再在圆中画出一个扇形并涂色。

四、图形计算题

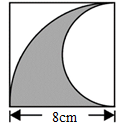
12．求涂色部分的面积。

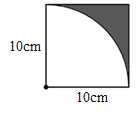
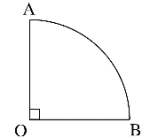
13．求阴影部分的面积（如下图，红色的部分是一个扇形）。

【能力提升】

五、解答题

14．在比赛中，铅球投掷的落点区域是一个圆，某运动员最远投掷距离为16米，铅球可能的落点区域面积是多少？

15．一个挂钟的时针长5厘米，分针长8厘米，从中午12时到下午3时，分针尖端“走了”多少厘米？时针“扫过”的面积是多少平方厘米？

【拓展实践】

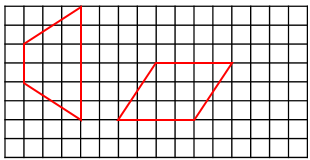
16．下图每个方格边长表示为1厘米，图中是一个梯形，按要求完成下面两个问题∶

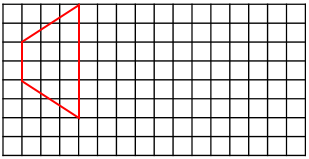
（1）计算梯形面积。

（2）在方格中画出一个与梯形面积一样大的平行四边形。

（3）以某一个方格交点为圆心，画一个半径4厘米，圆心角90度的扇形，计算扇形面积。

17．如图分别以长方形、平行四边形、梯形的四个顶点为圆心，画半径为1厘米的圆。求每个图形中阴影部分的面积。（取3.14）

（1）笑笑直接写出：3.14×12＝3.14（平方厘米），求出了每个图形中阴影部分的面积都是3.14平方厘米。

（2）你能理解笑笑的做法吗？并用学过的数学知识解释她这样算的道理。

（3）请你计算下面左图中阴影部分的面积、右图中阴影部分的周长。

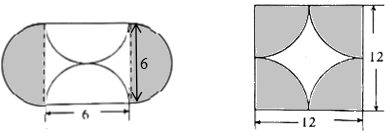
（4）反思：解决这些问题你有什么感悟？写出来分享给大家。

参考答案

1．B【分析】一条弧和经过这条弧两端的两条半径所围成的图形，叫做扇形，图中涂色部分就是扇形。

如图：

【详解】结合扇形的概念可知：

原题中选项B是扇形。

故答案为：B

【点睛】理解扇形的概念，明确其特点是解题关键。

2．C【分析】涂色部分的面积＝半径8cm的扇形面积－直径8cm的半圆面积，据此分别求出涂色部分和半圆面积，比较即可。

【详解】涂色部分：3.14×82÷4－3.14×（8÷2）2÷2

＝3.14×64÷4－3.14×16÷2

＝50.24－25.12

＝25.12（cm2）

半圆面积：3.14×（8÷2）2÷2

＝3.14×16÷2

＝25.12（cm2）

故答案为：C

【点睛】关键是掌握并灵活运用圆的面积公式，扇形面积＝圆的面积×。

3．B【分析】钟面上分针的长度是圆的半径，分针走一大格是5分钟，一大格是30°；那么15分钟要走3大格，30°×3是圆心角的度数；再根据扇形的定义：扇形是一条弧和经过这条弧两端的两条半径所围成的图形。据此判断。

【详解】15÷5＝3

30°×3＝90°

钟面上分针从12点整起，走15分钟所经过的部分是一个圆心角为90°，分针长为半径的扇形。

故答案为：B

【点睛】掌握扇形的定义是解题的关键。

4．A【分析】由圆的两条半径与这两条半径所夹的圆心角所对的弧围成的图形就是扇形。扇形面积＝πr²×，据此分析。

【详解】在同一个圆中，半径和直径不变，扇形的大小与这个扇形的圆心角有关。

故答案为：A

【点睛】关键是掌握扇形面积公式，扇形是圆的一部分。

5．D【分析】设一个扇形的半径为r，根据题意，两个扇形的半径比为1∶2，则另一个扇形的半径为2r，一个圆心角为n，则另一个圆心角为2n；根据扇形的面积公式：π×r 2×，求出两个扇形的面积，再根据比的意义，求出两个扇形的面积比，即可解答。

【详解】两个扇形的半径之比为1∶2，圆心角之比也为1∶2

设一个扇形的半径为r，则另一个为2r，一个圆心角为n，另一个圆心角为2n。

π×r2×∶[π×（2r）2×]

＝1∶（1×4×2）

＝1∶8

故答案选：D

【点睛】本题考查扇形面积公式的应用，关键是熟练掌握扇形面积公式。

6．扇形     12.56     50.24【分析】经过观察图形可知，这是一个扇形，根据扇形的周长公式求出半径，再根据圆的周长公式：C＝2πr，圆的面积公式：S＝πr2，把数据代入公式解答。

【详解】解：设半径为rdm。

2×3.14r÷4＋2r＝28.56

1.57r＋2r＝28.56

3.57r＝28.56

r＝8

2×3.14×8÷4

＝50.24÷4

＝12.56（dm）

3.14×82÷4

＝3.14×64÷4

＝50.24（dm2）

答：它的弧长（）是12.56dm，面积是50.24dm2。

【点睛】此题主要考查扇形的周长公式、圆的周长公式、圆的面积公式的灵活运用，关键是熟记公式。

7．45°##45度

16【分析】把一张圆形纸片对折一次，也就是把这个圆平均分成2份，对折两次，也就是把这个圆平均分成4份，对折三次，也就是把这个圆平均分成8份，周角是360°，用除法求出这个圆心角的度数，该圆的周长相当于这个圆心角所对的弧长的8倍，据此可以求出该圆的周长，根据圆的周长公式：，那么，把数据代入公式解答。

【详解】360°÷8＝45°

6.28×8÷3.14

＝50.24÷3.14

＝16（厘米）

【点睛】此题考查的目的是理解掌握扇形与圆之间的关系及用，圆的周长公式及应用，关键是明确：把这个圆形纸片对折三次，也就是把这个圆形纸片平均分成8份。

8．6.28【分析】根据三角形内角和是180°；三个内角拼成一个半圆；即三个扇形拼成一个半径是2cm的半圆；根据圆的面积公式：π×半径2，代入数据，求出圆的面积，再除以2，即可解答。

【详解】3.14×22÷2

＝3.14×4÷2

＝12.56÷2

＝6.28（cm2）

【点睛】解答本题的关键明确三角形内角和是180°，三个内角拼成一个平角；由此推导出三个扇形拼成半圆，进而解答。

9．942【分析】观察图形可知，扇面的面积等于圆心角是135°、半径30厘米的扇形的面积与圆心角是135°，半径30－20＝10厘米的扇形的面积之差，据此利用扇形的面积＝ ，代入数据计算即可解答问题。

【详解】30－20＝10（厘米）

－

＝－

＝1059.75－117.75

＝942（平方厘米）

【点睛】此题考查了扇形的面积公式的实际应用，熟记公式即可解答问题。

10．8     25.12     50.24     12.56【分析】根据同一个圆直径等于半径的2倍，根据圆的周长公式C＝πd，圆的面积公式S＝πr2，在这个圆中有一个圆心角为90°的扇形，这个扇形的面积等于整圆面积的。据此解答即可。

【详解】4×2＝8（cm）

3.14×8＝25.12（cm）

3.14×42＝50.24（平方厘米）

50.24×＝12.56（平方厘米）

则它的直径是8cm，周长是25.12cm，面积是50.24cm2。在这个圆中有一个圆心角为90°的扇形，这个扇形的面积是12.56cm2。

【点睛】本题考查圆的周长和面积，熟记公式是解题的关键。

12．见详解【分析】把圆规的两脚分开，定好两脚间距离为2厘米，把有针尖的一只脚固定在一点上，带有铅笔的那只脚绕点旋转一周，再画出半径和直径并用字母标出，将直径和半径所夹的扇形涂色即可。

【详解】

【点睛】本题主要考查了圆的画法，以及半径、直径和扇形的认识。掌握各概念的意义是解题的关键。

16．21.5cm2【分析】涂色部分的面积＝正方形面积－扇形面积，正方形面积＝边长×边长，扇形面积＝πr2×。

【详解】10×10－3.14×102×

＝100－3.14×100×

＝100－78.5

＝21.5（cm2）

13．18.24cm2【分析】观察图形可知，根据三角形的面积公式：S＝ah÷2，圆的面积公式：S＝πr2，扇形的面积公式：S＝πr2×，然后用三角形的面积减去红色扇形的面积即可求出左下空白部分的面积，然后用半径是8cm的圆的面积的一半减去左下空白部分的面积即可求出阴影部分的面积。

【详解】8×8÷2－3.14×82×

＝64÷2－3.14×64×

＝32－25.12

＝6.88（cm2）

3.14×（8÷2）2×－6.88

＝3.14×16×－6.88

＝25.12－6.88

＝18.24（cm2）

14．200.96平方米【分析】由题意可得，圆的半径是16米，根据圆的面积公式求出圆的面积，然后将圆的面积乘即可求出阴影部分的面积。

【详解】

＝50.24×16×

＝803.84×

＝200.96（平方米）

答：铅球可能的落点区域面积是200.96平方米。

【点睛】本题考查的是圆的面积公式，明确题目中16米是半径还是直径是解题的关键。

15．150.72cm；19.625平方厘米【分析】中午12时到下午3时，分针尖端“走了”3圈，根据圆的周长＝2πr，求出一圈周长，乘3即可；时针“扫过”圆，根据圆的面积＝πr²，求出圆的面积，乘即可。

【详解】2×3.14×8×3＝150.72（厘米）

3.14×5²×＝19.625（平方厘米）

答：分针尖端“走了”150.72厘米，时针“扫过”的面积是19.625平方厘米。

【点睛】关键是掌握圆的周长和面积公式。

16．（1）12平方厘米；

（2）见详解；

（3）图见详解，面积为12.56平方厘米【分析】（1）根据梯形的面积公式，直接计算即可；

（2）平行四边形的面积等于底乘高，当面积为12平方厘米时，可以取底为4厘米、高为3厘米，据此画图即可；

（3）根据题意，结合画扇形的方法，直接作图即可。这个扇形恰好是四分之一圆，据此先求出半径是4厘米圆的面积，再除以4，得到这个扇形的面积。

【详解】（1）（2＋6）×3÷2

＝8×3÷2

＝12（平方厘米）

答：梯形的面积是12平方厘米。

（2）

（3）

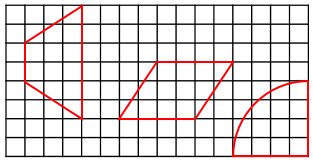
3.14×42÷4＝12.56（平方厘米）

答：这个扇形的面积是12.56平方厘米。

【点睛】本题考查了梯形和扇形的面积，灵活运用梯形和扇形的面积公式是解题的关键。

17．（2）理解，理由见详解；

（3）左图面积：28.26平方厘米，右图周长：85.68厘米；

（4）见详解【分析】（2）笑笑的做法是正确的，因为四边形内角和为360°，也就是4个扇形拼成一个圆，即长方形、平行四边形、梯形中阴影部分面积均等于同半径的圆的面积；

（3）左图中两侧的半圆，经过水平移动，能拼接成一个直径为6厘米的整圆，则S左图阴影＝3.14×（6÷2）2＝28.26（平方厘米）；

右图中阴影部分周长可看作一个直径为12厘米的圆的周长与一个边长为12厘米的正方形的周长之和，则C右图阴影＝3.14×12＋12×4＝85.68（厘米）；

（4）由以上解答可知：是把复杂分散的图形转化为简单集中的图形，从而便于计算其面积和周长。

【详解】（2）理解；

理由如下：

①长方形中阴影部分是4个圆心角为90°、半径为1的扇形，90°×4＝360°，则阴影部分面积相当于一个半径为1厘米的圆的面积，即：3.14×12＝3.14（平方厘米）；

②③平行四边形内角和＝（4－2）×180°＝360°，同理，平行四边形4个顶点上的阴影部分面积相当于半径为1厘米的圆的面积，即：3.14×12＝3.14（平方厘米）；梯形也是一样的道理。

（3）S左图阴影＝3.14×（6÷2）2

＝3.14×9

＝28.26（平方厘米）

C右图阴影＝3.14×12＋12×4

＝37.68＋48

＝85.68（厘米）

（4）我的感悟：数学要学会运用转化思想，把复杂的规律转化为简单易懂的知识。

【点睛】充分理解四边形内角和是360°，以及联想平移变换使图形组合为利于解题的形状；这些也是转化思想的体现。