海南省临高县2022-2023学年七年级下学期期中数学试题（含解析）

这是一份海南省临高县2022-2023学年七年级下学期期中数学试题（含解析），共17页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

海南省临高县2022-2023学年七年级下学期期中数学试题
学校:___________姓名：___________班级：___________考号：___________

一、单选题
1．在数－3.14， ， ， π， ， 0.1010010001……中无理数的个数有（    ）
A．3个 B．2个 C．1个 D．4个
2．如图所示的车标，可以看作由平移得到的是（    ）
A． B． C． D．
3．如果电影票上的“排号”记作，那么表示（　　）
A．排号 B．排号 C．排号 D．排号
4．在平面直角坐标系中，点所在的象限是（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
5．下列式子成立的是（　　）
A． B． C． D．
6．如图，点在的延长线上，下列条件中能判断的是（　　）

A． B． C． D．
7．下列命题中，是假命题的是（　　）
A．垂线段最短
B．两条直线被第三条直线所截，同位角相等
C．在同一平面内，垂直于同一直线的两条直线平行
D．经过直线外一点，有且只有一条直线与这条直线平行
8．估计与最接近的两个整数是（　　）
A．和 B．和 C．和 D．和
9．点P（-2，-3）向左平移1个单位，再向上平移3个单位，则所得到的点的坐标为（   ）
A．（-3，0） B．（-1，6） C．（-3，-6） D．（-1，0）
10．如图，三条直线相交于点O．若CO⊥AB，∠1=56°，则∠2等于(    )

A．30° B．34° C．45° D．56°
11．如图，，直线EF分别交AB，CD于点E，F，EG平分，若，则　　

A． B． C． D．
12．线l1∥l2，一块含30°角的直角三角板如图所示放置，∠1＝25°，则∠2等于（　　）

A．30° B．35° C．40° D．45°

二、填空题
13．的平方根是 ．
14．已知，则 ．
15．若点M（a + 5，a﹣3 ）在y轴上，则点M的坐标为 ，到x轴的距离为 ．
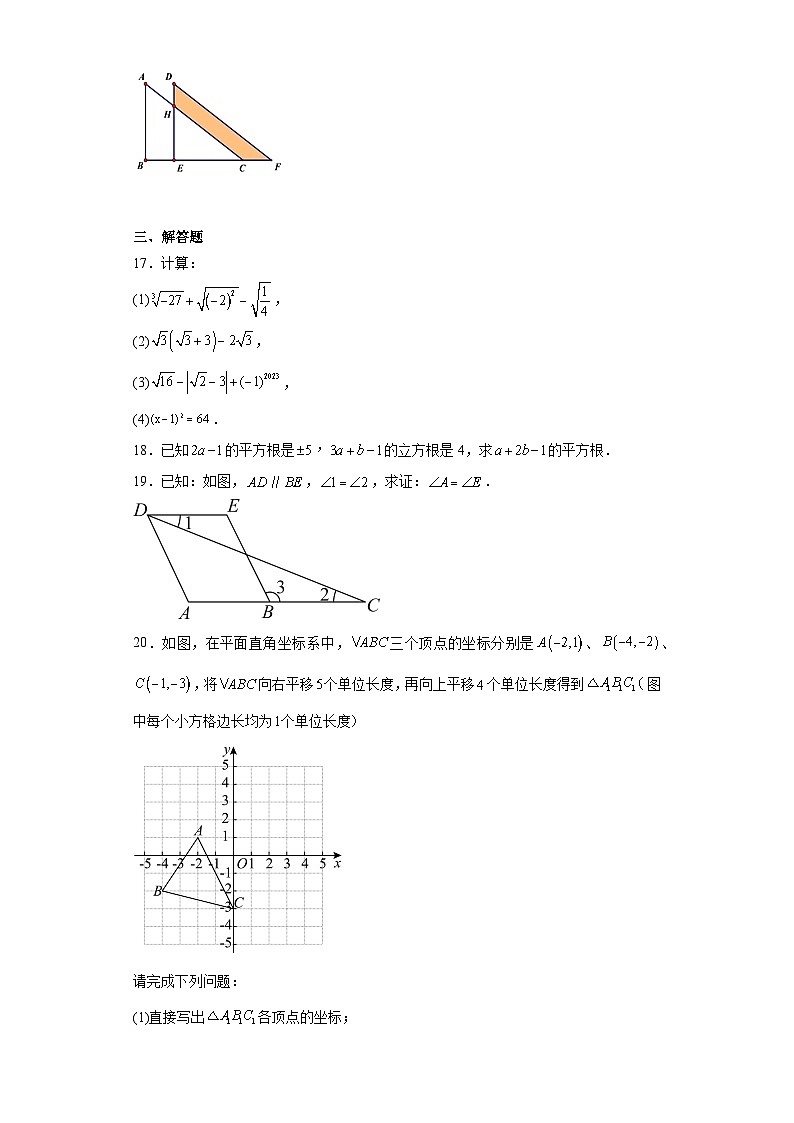
16．如图是重叠的两个直角三角形，将其中一个直角三角形沿BC方向平移BE的距离就得到此图，已知AB=8cm，BE=4cm,DH=3cm，则图中阴影部分的面积是 .                        


三、解答题
17．计算：
(1)，
(2)，
(3)，
(4)．
18．已知的平方根是 的立方根是4，求的平方根．
19．已知：如图，，，求证：．  

20．如图，在平面直角坐标系中，三个顶点的坐标分别是、、，将向右平移个单位长度，再向上平移个单位长度得到图中每个小方格边长均为个单位长度

请完成下列问题：
(1)直接写出各顶点的坐标；
(2)作出平移之后的图形；
(3)求出的面积．
21．如图，点D、F在线段AB上，点E、G分别在线段BC和AC上，CDEF，∠1＝∠2．
（1）判断DG与BC的位置关系，并说明理由；
（2）若DG是∠ADC的平分线，∠3＝85°，且∠DCE∶∠DCG＝9∶10，试说明AB与CD有怎样的位置关系？

22．已知，点B为平面内一点，于B．
(1)如图，直接写出和之间的数量关系．

(2)如图，过点B作于点D，求证：．

(3)如图，在（2）问的条件下，点E，F在DM上，连接BE，BF，CF，BF平分，BE平分，若，，求的度数．


参考答案：
1．A
【分析】直接利用无理数定义直接判断即可.
【详解】解：－3.14， ，0，π，，0.1010010001……中无理数有，π，0.1010010001……共三个．
故选：A．
【点睛】本题考查无理数的判断，基础知识牢固是解题关键.
2．B
【分析】根据平移的概念：在平面内，把一个图形整体沿某一方向移动，这种图形的平行移动，叫做平移变换，简称平移，即可选出答案．
【详解】解：根据平移的概念可知四个车标中只有B选项中的车标是经过平移得到的，
故选B．
【点睛】本题主要考查了图形的平移，在平面内，把一个图形整体沿某一方向移动，叫做平移，掌握平移的定义是解题关键．
3．C
【分析】由于将“排号”记作，根据这个规定即可确定表示的点．
【详解】解：∵“排号”记作，
∴表示排号．
故选：C．
【点睛】此题主要考查了根据坐标确定点的位置，解题关键是理解题目的规定，知道坐标与位置的对应关系．
4．D
【分析】根据点的坐标判断所在的象限即可．
【详解】解：点，
点位于第四象限，
故选：D．
【点睛】本题考查了点的坐标，掌握如果点位于第四象限，则，是解题的关键．
5．D
【分析】根据立方根，平方根，算术平方根进行计算，逐一判断即可解答．
【详解】解：、，故A不符合题意；
B、，故B不符合题意；
C、无意义，故C不符合题意；
D、，故D符合题意；
故选：．
【点睛】本题考查了立方根，平方根，算术平方根，熟练掌握立方根，平方根以及算术平方根的意义是解题的关键．
6．C
【分析】根据平行线的判定方法逐项判断即可．
【详解】解：当时，根据同位角相等，两直线平行可得，无法判断，故此选项不符合题意；
B.当时，无法判断，故此选项不符合题意；
C.当时，根据内错角相等，两直线平行可得，故此选项符合题意；
D.当时，根据内错角相等，两直线平行可得，无法判断，故此选项不符合题意．
故选：．
【点睛】本题主要考查平行线的判定，熟练掌握平行线的判定方法是解题关键．
7．B
【分析】利用垂线段的性质、平行线的性质及判定方法分别判断后即可确定正确的选项．
【详解】解：A、垂线段最短，原命题是真命题，不符合题意；
B、两条平行直线被第三条直线所截，同位角相等，原命题是假命题，符合题意；
C、在同一平面内，垂直于同一直线的两条直线平行，原命题是真命题，不符合题意；
D、经过直线外一点，有且只有一条直线与这条直线平行，原命题是真命题，不符合题意．
故选：B．
【点睛】本题考查了命题与定理的知识，解题的关键是了解有关的定义及定理，难度不大．
8．A
【分析】根据得，则，即可得．
【详解】解：∵，
∴，

与最接近的两个整数是和，
故选：A．
【点睛】本题考查了运用算术平方根知识对无理数进行估算的能力，关键是能准确理解并运用该知识．
9．A
【详解】∵点P（-2，-3）向左平移1个单位后坐标为（-3，-3），（-3，-3）向上平移3个单位后为（-3，0），
∴点P（-2，-3）向左平移1个单位，再向上平移3个单位，所得到的点的坐标为（-3，0），
故选：A．
10．B
【分析】根据垂线的定义求出∠3，然后利用对顶角相等解答．
【详解】解：∵CO⊥AB，∠1=56°，
∴∠3=90°﹣∠1=90°﹣56°=34°，
∴∠2=∠3=34°．
故选B．

【点睛】本题考查垂线定义，余角性质，对顶角性质，掌握垂线定义，余角性质，对顶角性质是解题关键．
11．C
【分析】根据两直线平行，同旁内角互补，可求出的度数，再根据角平分线的性质，可得到的度数，然后用两直线平行，内错角相等求出的度数．
【详解】，
，，
又平分，
，
故．
故选C．
【点睛】本题考查了平行线的性质，解题的关键是掌握：两直线平行，内错角相等；两直线平行，同旁内角互补．
12．B
【分析】先根据三角形外角的性质求出∠3的度数，再由平行线的性质得出∠4的度数，由直角三角形的性质即可得出结论．
【详解】解：∵∠3是△ADG的外角，
∴∠3=∠A+∠1=30°+25°=55°，
∵l1∥l2，
∴∠3=∠4=55°，
∵∠4+∠EFC=90°，
∴∠EFC=90°﹣55°=35°，
∴∠2=35°．
故选：B．

【点睛】本题考查的是平行线的性质及三角形外角的性质，用到的知识点为：两直线平行，同位角相等．
13．±3
【分析】根据算术平方根、平方根解决此题．
【详解】解：，
实数的平方根是．
故答案为：．
【点睛】本题主要考查算术平方根、平方根，熟练掌握算术平方根、平方根是解题的关键．
14．1
【分析】根据绝对值和算术平方根的非负性求出a，b的值，代入代数式求值即可．
【详解】解：∵，|a＋1|≥0，≥0，
∴a＋1＝0，2−b＝0，
∴a＝−1，b＝2，
∴．
故答案为：1．
【点睛】本题考查求算术平方根，绝对值和算术平方根的非负性，掌握几个非负数的和为0，则这几个非负数分别等于0是解题的关键．
15． （0,-8） 8
【分析】由题意得:a+5=0,解方程可得a的值,代入点M（a+5,a-3）可得M的坐标,进而可得到x轴的距离为8．
【详解】解:由题意得:a+5=0,
解得a=-5, 则点M的坐标为（0,-8）,
到x轴的距离为8,
故答案为:（0,-8）;8.
【点睛】本题主要考查点的坐标,解决本题的关键是掌握纵轴上的点横坐标为0．
16．26cm2
【详解】分析：根据平移的性质可知：AB=DE，BE=CF；由此可求出EH和CF的长．由于CH∥DF，根据平行线分线段成比例，可求出EC的长．已知了EH、EC，DE、EF的长，即可求出△ECH和△EFD的面积，进而可求出阴影部分的面积．
详解：由平移的性质知，  
∴
∵HC∥DF∴

又∵，
∴
∴
∴
故答案为
点睛：考查平移的性质，平行线分线段成比例定理，掌握平移的性质是解题的关键.
17．(1)
(2)
(3)
(4)或

【分析】（1）首先计算开平方和开立方，然后从左向右依次计算，求出算式的值即可；
（2）首先计算乘法，然后从左向右依次计算，求出算式的值即可；
（3）首先计算乘方、开平方和绝对值，然后从左向右依次计算，求出算式的值即可；
（4）根据平方根的含义和求法，求出的值，进而求出的值即可．
【详解】（1）解：原式
；
（2）解：原式
；
（3）解：原式

；
（4）解：或，
解得或．
【点睛】此题主要考查了平方根的含义和求法，实数的混合运算，掌握运算的步骤是解题的关键．
18．
【分析】根据题意得，，解得：，，将，代入进行计算，最后求其平方根即可．
【详解】解：∵的平方根是，的立方根是4，
∴，，
解得：，，
∴，
∴的平方根为．
【点睛】本题考查了平方根，立方根，解题的关键是掌握平方根和立方根，正确计算．
19．见解析
【分析】根据，可得，根据平行线的性质可得，根据已知可得，等量代换即可得证．
【详解】证明：∵，
∴，
∴，
∵，
∴
∴．
【点睛】本题考查了平行线的性质与判定，熟练掌握平行线的性质与判定是解题的关键．
20．(1)，，
(2)见解析
(3)

【分析】利用平移变换的性质写出坐标；
根据点的坐标，作出三角形即可；
把三角形的面积看成矩形的面积减去周围的三个三角形面积即可．
【详解】（1）解：根据平移可得，的各点横坐标加，纵坐标加可得：，，；
（2）如图，即为所求；

（3）．
【点睛】本题考查作图平移变换，三角形的面积等知识，解题的关键是掌握平移变换的性质，学会用分割法求三角形面积．
21．（1），理由见解析；（2）CD⊥AB
【分析】（1）利用平行线的性质，可得，根据题意可得，根据平行线的判定定理：内错角相等，两直线平行，即可证明；
（2）根据（1）DG∥BC性质（两直线平行，同旁内角互补）可得，利用角比值的计算方法，可求得，由（1）得：，根据角平分线的性质即可得：，即CD⊥AB．
【详解】解：（1）DG∥BC．
理由：∵CD∥EF，
∴，
∵，
∴，
∴DG∥BC；
（2）．
理由：∵由（1）知DG∥BC，，
∴，
∵，
∴，
∴，
∵DG是∠ADC的平分线，
∴，
∴CD⊥AB．
【点睛】本题主要考查平行线的判定及性质、角度比值的计算、角平分线的定义等，对平行线判定及性质的融会贯通是解题关键．
22．(1)
(2)证明见解析
(3)

【分析】（1）根据平行线的性质及直角三角形的性质证明即可；
（2）过点B作，根据同角的余角相等得出，再根据平行线的性质得到，即可得到；
（3）过点B作，根据角平分线的定义得出，设，，可得，再根据，得到，解方程得到，继而得出，．
【详解】（1）如图1，

∵，
∴，
∵，
∴，
∴，，
故答案为：；
（2）如图2，过点B作，

∵，
∴，
∴，
∴，
∵，
∴，
∴，
∵，
∴，．
（3）如图3，过点B作，

∵BF平分，BE平分，
∴，，
由（2）知，
∴，设，，
则，，，
，
∴
∵，，
∴，
中，由得
，
∵，
∴，
∴，
∴，
∴．
【点睛】本题考查平行线的性质与应用、角平分线的性质、方程思想等知识，学会添加辅助线，掌握相关知识是解题关键．