四川省成都市大邑县2022-2023学年八年级上学期期末数学试题（含答案）

这是一份四川省成都市大邑县2022-2023学年八年级上学期期末数学试题（含答案），共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
八年级质量检测
数 学
考试时间120分钟，满分150分
A卷（共100分）
第I卷（选择题，共32分）
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只一项符合题目要求，答案涂在答题卡上）
1. 下列各数中，无理数是（ ）
A. B. C. 0.6 D. 5.212121
2. 如图，以直角三角形的三边为边向外作正方形，根据图中数据，可得出正方形的面积是（ ）

A. 12 B. 24 C. 30 D. 10
3. 若点关于轴对称，则的值分别为（ ）
A. B. C. D.
4. 李强是一名足球爱好者，2022年卡塔尔世界杯期间，他随机统计了20名各国参加世界杯赛人员的年龄，并制成如下统计表，则他们年龄的中位数和众数分别是（ ）
年龄（岁）
24
26
30
34
38
42
人数
3
5
4
2
3
3
A. 26，34 B. 30，26 C. 38，42 D. 32，24
5. 若为实数，且与互为相反数，则的平方根为 （ ）
A. B. C. D.
6. 如图，在中，平分，平分，，则 （ ）

A. 126° B. 54° C. 102° D. 108°
7. 下列命题中，假命题是（ ）
A. 实数和数轴上的点是一一对应的
B. 是一组勾股数
C. 有公共顶点且相等的两个角是对顶角
D. 函数中自变量的取值范围是
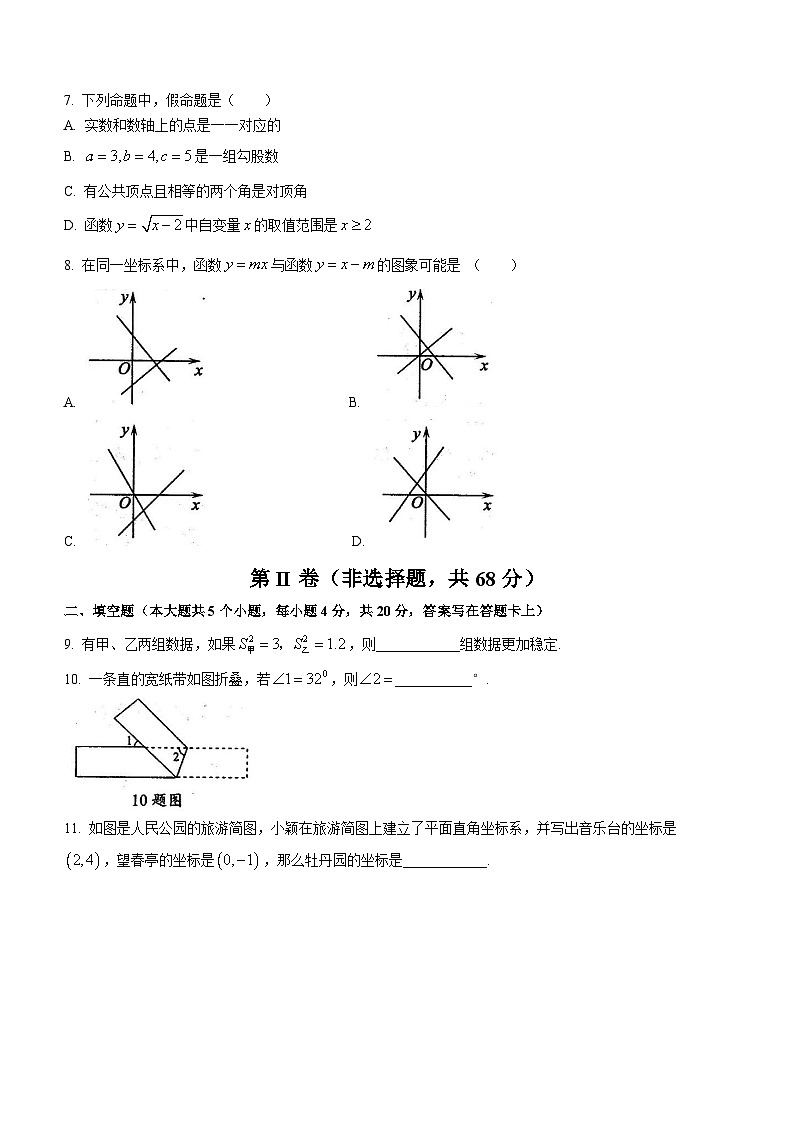
8. 在同一坐标系中，函数与函数的图象可能是 （ ）
A. B.
C. D.
第II卷（非选择题，共68分）
二、填空题（本大题共5个小题，每小题4分，共20分，答案写在答题卡上）
9. 有甲、乙两组数据，如果，则____________组数据更加稳定.
10. 一条直的宽纸带如图折叠，若，则___________°.

11. 如图是人民公园的旅游简图，小颖在旅游简图上建立了平面直角坐标系，并写出音乐台的坐标是，望春亭的坐标是，那么牡丹园的坐标是____________.

12.河滨公园有一块长方形的草坪如图所示，有少数的人为了避开拐角走“捷径”，在草坪内走出了一条“路”，他们仅仅少走了___________米，却踩伤了花草！青青绿草地，悠悠关我心，请大家文明出作，足下留“青”!

13. 如图，等边的边长为1，是边上一点，过点作于点，若，则与的函数关系式为_____________.

三、解答题（本大题共5个小题，共48分，解答过程写在答题卡上）
14.（本小题满分12分，每题6分）
（1）计算：
（2）解方程组：
15.（本小题满分8分）
列方程组解应用题：为了丰富学生的课外体育活动，八年级2班需要购买排球和跳绳.根据下列对话，求出肖雨所购买的排球和跳绳的单价.

16. （本小题满分8分）
某商场准备开展元旦促销活动，现采用移动车进行广播宣传，如图，移动广播车的笔直的公路上以200米/分的速度沿方向行驶，张丽的家在公路的一侧，到公路的距离.假如移动广播车周围500米以内能听到广播宣传，张丽在家能够听到广播宣传吗？若能，请求出她总共能听到多长时间的广播宣传？若不能，请说明理由.

17.（本小题满分10分）
学校坚持“德育为先、智育为重、体育为基、美育为要、劳动为本”的五育并举育人理念，拟开展校级优秀学生评比活动.下表是八年级1班三名同学综合素质考核的得分表：（每项满分10分）
姓名
行为规范
学习成绩
体育成绩
艺术获奖
劳动卫生
李铭
10
10
6
9
7
张晶晶
10
8
8
9
8
王浩
9
7
9
8
9
（1）如果根据五项考核的平均成绩确定推荐1人，那么被推荐的是__________；
（2）你认为表中五项考核成绩中最重要的是__________；请你设定一个各项考评内容的占分比例（比例的各项须满足：①均为整数；②总和为10；③不全相同），按这个比例对各项的得分重新计算，比较出大小关系，并从中推荐得分最高的作为校优秀学生的侯选人.
18.（本小题满分10分）
已知直线平行于直线，且过点.
（1）求直线的解析式；
（2）在下面的坐标系中，画出直线和的图象，并根据图象直接写出方程组的解；
（3）若直线与轴的交点为，直线和的交点为，以为边作，在第一象限是否存在点，使是的面积为面积的2倍？若存在，请求出符合条件的点的坐标；若不存在，请说明理由.


B卷（共50分）
一、填空题（本大题共5个小题，每小题4分，共20分，答案写在答题卡上）
19. 正整数分别满足，则_________________.
20. 《孙子算经》是我国古代一部较为普及的算书，许多问题浅显有趣.其中下卷第31题“雉兔同笼”流传尤为广泛 ，漂洋过海流传到了日本等国.“雉兔同笼”题为：“今有雉（鸡）兔同笼，上有三十五头，下有九十四足.问雉兔各几何？”设雉（鸡）有只，兔有只，则可列方程组为_______________.
21. 如图是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形拼接而成的.已知，正方形的面积为80.连接，交于点，交于点，连接.则图中阴影部分的面积之和为_____________.

22. 在平面直角坐标系中，对于两点给出如下定义：若点到轴的距离中的最大值等于点到轴的距离中的最大值，则称两点为“等距点”.已知点两点为“等距点”，则_____________.
23. 如图，平面直角坐标系中，点分别在轴，轴的负半轴上，，且.交轴于点交轴于点，若平分，则线段之间的数量关系是___________.

二、解答题（本大题共3个小题，共30分，解答过程写在答题卡上）
24.（本小题满分8分）
如图，一列快车从甲地匀速驶往乙地，一列慢车从乙地匀速驶往甲地，两车同时出发，设慢车行驶的时间为，两车之间的距离为，图中的折线表示与之间的函数关系.根据图象解决下列问题.
（1）求慢车和快车的速度；
（2）求线段所表示的与之间的函数关系式，并写出自变量的取值范围.

25.（本小题满分10分）
【基础巩固】
（1）如图1，点在线段上，.
求证：.
【尝试应用】
（2）如图2，，若是的中点，，求的长.
【拓展提高】
（3）如图3，，是的中点，，求的长.

26.（本小题满分12分）
在平面直角坐标系中，直线分别交轴，轴于两点，.
（1）如图1，点在线段上，点在线段上，于点，于点，若，求证：；
（2）在（1）的条件下，求直线的函数表达式；
（3）如图2，若，点分别是（2）中直线和线段上的动点，求周长最小值的平方.





















参考答案
A卷（共100分）
一、选择题
1—4 ABCB 5—8 DACD
二、填空题
9. 乙 10. 74 11. 12. 6 13.
三、解答题
14.（1）解：原式
；
（2）解：
①×3得： ④，
②-④得：
解得：
把代入①得：，
∴原方程组的解为
15. 解：设排球每个元，跳绳每根元，由题意得：

解这个方程组得：
答：排球每个24元，跳绳每根18元.
16. 解：

如图，当时，张丽在家开始听到广播声音，当广播车移动到点，时，广播声音结束.
在中，，
由勾股定理得：，
同理，，
∴（分钟）
∴张丽在家听到移动车广播声音，她听到广播声音的时间为4分钟.
17. 解：（1）张晶晶；
（2）（答案中唯一）学习成绩，
设行为规范：学习成绩：体育成绩：艺术获奖：劳动卫生=2：4：2：1：1，
（答案不唯一，只要学生设置的权重与第一空一致，可得2分，若权重设置不为整数，则此步不给分）
则李铭的平均成绩为：（分）
张晶晶的平均成绩为：（分）
王浩的平均成绩为：（分）
根据我的设计比例，推荐李铭同学.
（按照学生设置的权重，算对一个给1分，推举出人选给1分，若最高分相等，可同时推选）
18. 解：（1）∵直线平行于直线，
∴
∴直线为且过点，
∴
∴，
∴；
（2）直线和的图象如图所示，
由图象可知的解为；
（3）如图，，
设，则，
∵，
∴，
当时，
，
∴，
∴；
当时，

∴，
∴，
当时，
情况不符，舍去，
∴或.
B卷（共50分）
一、填空题
19. 81 20. 21. 16
22. 1或2（填对一个得2分，见错不给分） 23.
二、解答题
24. 解：（1）由图象可知全程1200千米，慢车走完全程用了15时，
∴慢车的速度为千米/时，
设快车的速度为千米/时，由题意得：

∴
∴快车和慢车的速度分别是120千米/时，80千米/时；
（2）由图象可知，点表示快车已到达终点站，
∴快车所用的时间为，
此时两车相距千米，
∴，
又∵，
设为：，
∴，
解之得：
∴，
自变量的取值范围为：（或）.
25. 解：（1）证明：∵，
∴，
∴，
又∵，
∴；
（2）

如图2，延长交于点，
则，
∵是的中点，∴，
，
∴，
∴，
∵，
∴；
（3）如图3，过点作，交的延长线于点，连接，
同理可证，
∴，
过点作于点，
∵，
∴，
在中，，
，
∴，
在中，，
同理可证，
∴.

26. 解：（1）

∵，
∴，
∵，
∴，
则和均等腰直角三角形，
又∵，
∴，
∵在和中，
，
∴，
∴；
（2）设，
则，
作中，有，
∴，
即，
解得：，
∴，
∴，
∵，∴，
设直线为：，
∴，
解得：，
∴；
（3）

如图2，作点关于直线的对称点，连结，
∵，∴，
∵，
∴，
作点关于轴的对称点，则，
∴，
∴周长最小值即为线段的长，
∴，
∴周长最小值的平方为.