数学人教版2.1 整式优质ppt课件

这是一份数学人教版2.1 整式优质ppt课件，共22页。PPT课件主要包含了常数项，次数最高项，单项式，多项式，用字母表示，a+b，ar–r²，x–21，x²–2x5，其中5是常数项等内容，欢迎下载使用。
教学目标1.通过本节课的学习，使学生掌握整式、多项式的项及其次数、常数项的概念.2.知道整式和单项式、多项式的关系.教学重难点重点：掌握整式及多项式的有关概念.难点：多项式的次数.
1.几个单项式的 叫做多项式，多项式中的每个单项式叫做多项式的 ，不含字母的项叫做 .2.多项式里， 的次数，叫这个多项式的次数.3. 与 统称整式.
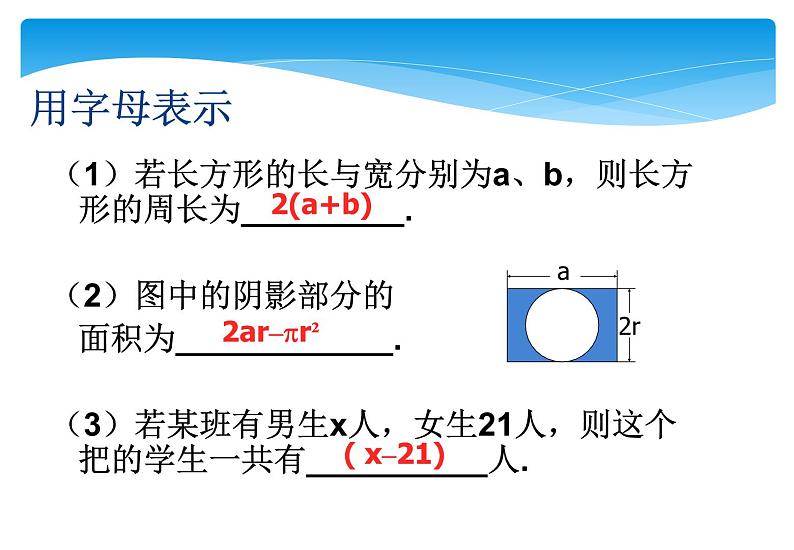
（1）若长方形的长与宽分别为a、b，则长方形的周长为_________. （2）图中的阴影部分的 面积为____________.（3）若某班有男生x人，女生21人，则这个把的学生一共有__________人.
问题2：它们与单项式有什么关系？
问题1 ：你所填入的代数式有什么共同特点？
上面这些式子都是由几个单项式相加而成的.
像这样，几个单项式的和叫做多项式。
在多项式中，每个单项式叫做多项式的项。
其中，不含字母的项，叫做常数项。
例如，多项式3x²–2x+5有三项，它们是
一个多项式含几项，就叫几项式。多项式里次数最高项的次数，就是这个多项式的次数。
例如，多项式3x²–2x+5是
（1）几个单项式的和叫做_________.
（2）在多项式中，每个单项式叫做___________.
（3）在多项式中，不含字母的项叫做 _______.
（4）在多项式中，次数最高的项的次数，叫做这个______________.
（5）多项式的每一项是否包括它前面的符号？
（6）单项式的次数与多项式的次数有什么区别？
多项式的每一项都包括它前面的符号，有正号也有负号。
单项式的次数是所有字母的指数的和；多项式的次数不是所有项的次数和。
知识点1 多项式的有关概念
定义：单项式与多项式统称整式．
知识点2 整式及简单应用
解析：根据多项式、整式的定义进行判断.
例2：指出下列多项式的项和次数，并说明它是几次几项式.（1）a3-a2b+ab2-b+3；(2)3n4-2n2+1.
解析：根据概念来确定，注意不要漏掉常数项.
解：（1）多项式a3-a2b+ab2-b+3的项是a3、-a2b、ab2、-b、3,共五项，次数是3，它是三次五项式；（2）多项式3n4-2n2+1的项是3n4、-2n2、1，共三项，次数是4，它是四次三项式.
例3：已知关于x的多项式（a+4）x4+(b-2)x3-2(a-1)x2+ax-3中不含x3项和x2项，试求当x=-1时，这个多项式的值.
解析：多项式中不含某一项或缺某一项是指在多项式中这一项不存在，即这一项的系数为0.
解：由题意得b-2=0,a-1=0，解得a=1,b=2.代入多项式为5x4+x-3,当x=-1时，5x4+x-3=5×(-1)4+（-1）-3=5-1-3=1
例4：某百货商场经销一种儿童服装，每件售价50元，每天可以销售80件，每件可盈利10元.为了迎接六一，商场决定采取适当的降价措施，扩大销售量，让利消费者.经市场调查发现：童装每降价1元，平均每天可多销售10件.（1）当每件降价x元（x＜10）时，每天该种服装的营业额是多少元？（2）当x=5时，每天的营业额是多少元？
解析：每天营业额=每天销售的件数×每件的售价.
解：（1）降价x元时，售价为（50-x）元，销售件数为（80+10x）件，因此每天该种服装的营业额是（50-x）(80+10x)元；
（2）当x=5时，（50-x）(80+10x)=(50-5)(80+10×5) =45×（80+50）=45×130=5850（元）.
8.当x=10，y=9时，代数式x2－y2的值是 .9.多项式3a2y－4ay3－1最高次项是 ，常数项是 .
本课时学习了多项式的有关知识，与前一节课所学的单项式合起来统称整式。