初中数学北师大版八年级上册第五章 二元一次方程组6 二元一次方程与一次函数课后测评

这是一份初中数学北师大版八年级上册第五章 二元一次方程组6 二元一次方程与一次函数课后测评，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

5.6 二元一次方程与一次函数

一、选择题
1．直线与直线的交点为（       ）
A． B． C． D．
2．如果直线与交点坐标是（a，b），则是下面哪个方程组的解（       ）
A． B． C． D．
3．如图，直线y＝x+5和直线y＝ax+b相交于点P，观察其图象可知方程x+5＝ax+b的解（　　）

A．x＝15 B．x＝25 C．x＝10 D．x＝20
4．在平面直角坐标系中，一次函数与的图象的交点在（       ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
5．已知直线与交点的坐标为，则方程组的解是（       ）
A． B． C． D．
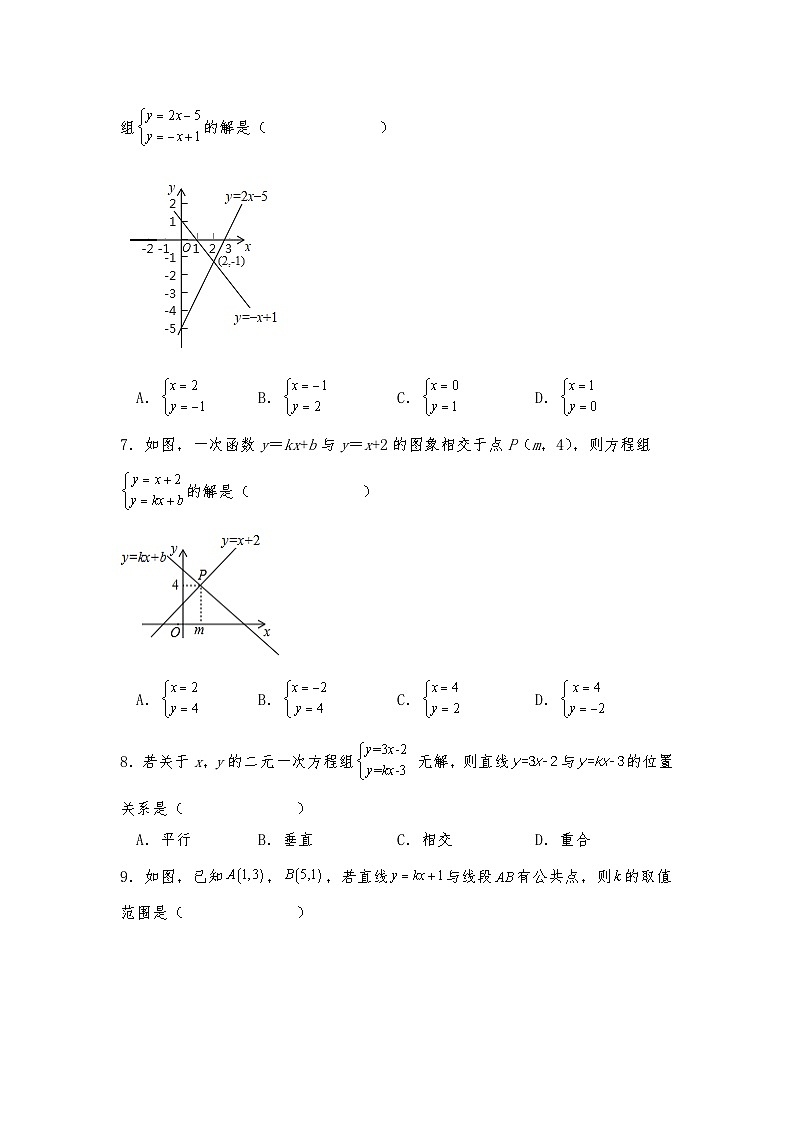
6．如图所示，在直角坐标系中的两条直线分别是和，那么方程组的解是（       ）

A． B． C． D．
7．如图，一次函数y＝kx+b与y＝x+2的图象相交于点P（m，4），则方程组的解是（       ）

A． B． C． D．
8．若关于x，y的二元一次方程组 无解，则直线与的位置关系是（       ）
A．平行 B．垂直 C．相交 D．重合
9．如图，已知，，若直线与线段有公共点，则的取值范围是（       ）

A． B． C． D．
10．已知直线与交于点，若与轴交于点， 是轴上一点，且，则点的横坐标为（　　）
A． B． C．或 D．或
11.如图，在平面直角坐标系中，直线与直线相交于点A，则关于x，y的二元一次方程组的解是（       ）

A． B． C． D．
12.在同一平面直角坐标系中，直线与相交于点，则关于x，y的方程组的解为（       ）
A． B． C． D．
13.在同一平面直角坐标系中，一次函数与的图象如图所示，小星根据图象得到如下结论：

①在一次函数的图象中，的值随着值的增大而增大；
②方程组的解为；
③方程的解为；
④当时，．
其中结论正确的个数是（       ）
A．1 B．2 C．3 D．4

二、填空题
1．如图，一次函数与交于点A，则方程组的解是______．

2．如果直线y＝x＋n与直线y＝mx－1的交点坐标为（1，－2），那么m＝________，n＝________．
3．已知二元一次方程组的解为，则图中三角形ABC的面积为_______．

4．若一次函数与的图象交点恰好在一次函数的图象上，则方程组
的解为________．
5.已知一次函数y=3x-1与y=kx（k是常数，k≠0）的图象的交点坐标是（1，2），则方程组的解是_________．

三、解答题
1．在平面直角坐标系xoy中，一次函数的图象是由函数y＝2x的图象向下平移5个单位得到的．解答下列问题：
(1)直接写出k和b的值；
(2)分别写出一次函数与x轴交点A和y轴交点B的坐标；
(3)求△AOB的面积．











2．如图，直线l1的函数表达式为y＝x+2，且l1与x轴交于点A，直线l2经过定点B（4，0），C（﹣1，5），直线l1与l2交于点D．

(1)求直线l2的函数表达式；
(2)求△ADB的面积；
(3)在x轴上是否存在一点E，使△CDE的周长最短？若存在，请直接写出点E的坐标；若不存在，请说明理由．









3．如图，直线l1：y＝﹣2x+4与x轴，y轴分别交于A，B两点，直线l2：y＝﹣x﹣3与x轴，y轴分别交于C，D两点．
（1）求四边形ABCD的面积；
（2）设直线l1，l2交于点P，求△PAD的面积．








4．如图，已知一次函数y=﹣x+8的图象与x轴、y轴分别相交于点A、B，与一次函数y=x的图象相交于点C．

（1）求点C坐标．
（2）若点Q在直线AB上，且△OCQ的面积等于12，请求出点Q的坐标．
（3）小明在探究中发现：若P为x轴上一动点，将线段PC绕点P按顺时针方向旋转90°得线段PC'，在点P的运动过程中，点C′始终在某一直线上运动．请直接写出该直线所对应的函数关系式：　 ．











5.如图1，在平面直角坐标中，直线：与抽交于点，直线：与轴交于点，与相交于点．

（1）请直接写出点，点，点的坐标：_________，________，_______．
（2）如图2，动直线分别与直线、交于、两点．
①若，求的值；
②若存在，求出此时点的坐标；若不存在，请说明理由．





6．如图，在平面直角坐标系中，直线AB：y=kx+b交y轴于点A（0，1），交x轴于点B（3，0）.平行于y轴的直线x=1交AB于点D，交x轴于点E，点P是直线x=1上一动点，且在点D的上方，设P（1，n）.

（1）求直线AB的表达式；
（2）求△ABP的面积（用含n的代数式表示）；
（3）当S△ABP=2时，以PB为边在第一象限作等腰直角三角形BPC，直接写出点C的坐标.


答案
一、选择题

B．D．D．A．C．A．A．A．D．C．B．C．B
二、填空题
1.． 2.-1；－． 3.24 4.． 5.．
三、解答题
1.(1)
解：∵一次函数的图象是由函数y＝2x的图象向下平移5个单位得到的．
∴一次函数的解析式为，
∴k＝2，b＝-5；
(2)
解：当时，，
当时，，解得，
∴点 ，；
(3)
解：∵点 ，，
∴，，
∴．
2.(1)
解：设l2的解析式是y=kx+b，
根据题意得：，解得：，
则函数的解析式是：y=-x+4；
(2)
解：在y=x+2，中令y=0，解得：x=-4，则A的坐标是（-4，0）．
解方程组，得：，
则D的坐标是（．
则S△ADB=×=；
(3)
解： D（2，2）关于x轴的对称点是D′（2，-2），
则设经过（2，-2）和点C的函数解析式是y=mx+n，
则，
解得：，
则直线的解析式是y=-x+．
令y=0，-x+=0，解得：x=．
则E的坐标是（，0）．

3.解：（1）当x=0时，y＝﹣2x+4=4；当y=0时，﹣2x+4=0，x=2，
∴A（2，0），B（0，4）；
∴OA＝2，OB＝4；
当x=0时，=-3；当y=0时，，x=-6，
∴C（﹣6，0），D（0，﹣3）；
∴OC＝6，OD＝3，
∴AC＝2+6＝8，
∴S四边形ABCD＝AC×OB+AC×OD
＝×8×（4+3）＝28；
（2）根据题意可知：，
解这个方程组得：，
∴P（，），
∴S△PAD＝S△PBD﹣S△ABD
＝×7×+×7×2
＝．
4.（1）由方程组得，
∴点C的坐标为（4，3）；
（2）∵一次函数的图象与x轴、y轴分别相交于点A、B，
∴A（，0），B（0，8），
∵点Q在直线AB上，
∴设Q（x，），
当Q点在C的上方时，S△OCQ=S△OBC﹣S△OBQ=12，
∴×8×4﹣=12，解得，x=1，
∴此时Q的坐标为（1，）；
当Q点在线段AC上时，
S△OAC=××3=9.6<12，不存在，舍去；
当Q点在A的下方时，S△OCQ=S△OAC+S△OAQ=12，
∴××3+=12，解得，x=7，
∴此时Q的坐标为（7，﹣），
故Q点的坐标为（1，）或（7，﹣）；
（3）设P的坐标为（m，0），作CM⊥x轴于M，C′N⊥x轴于N，

∵C（4，3），
∴OM=4，CM=3，
∴PM=，
∵∠CPM+∠C′PN=90°=∠CPM+∠PCM，
∴∠C′PN=∠PCM，
在△PCM和△C′PN中，
，
∴△PCM≌△C′PN（AAS），
∴PN=CM=3，C′N=PM=4﹣m，
∴ON=3+m，
∴C′（3+m，m﹣4），
∴点C′始终在直线上y=x﹣7运动，
故答案为：y=x﹣7．
5.（1）对于直线l2：y=3x-3①，
令y=3x-3=0，解得x=1，故点B（1，0），
对于l1：y=x+1，同理可得：点A（-1，0），
则，解得，
故点C的坐标为（2，3），
故答案为：（-1，0）、（1，0）、（2，3）；
（2）①点P在直线l1上，则设点P（t，t+1），同理点Q（t，3t-3），
则PQ=|t+1-3t+3|=2，
解得t=1或3；
②当点Q在x轴下方时，如下图，

设直线l1交y轴于点K，过点B作直线n∥AC交y轴于点N，
在y轴负半轴取点M使NM=2NK，过点M作直线m∥AC交l2于点Q，则点Q为所求点，
理由：∵M、Q在直线m上，且m∥AC，
∴S△MAC=S△QAC，
同理S△NAC=S△BAC，
∵MN=2KN，则m、l1之间的距离等于2倍n、l1之间的距离，
∴S△AQC=2S△ABC，
由直线l1的表达式知点K（0，1），
设直线n的表达式为y=x+b，将点B的坐标代入上式并解得b=-1，
∴ N（0，-1），
∵NK=1-（-1）=2，
∴MN=NK=2，
∴M（0，-3），
在直线m的表达式为y=x-3②，
联立①②解得，
∴Q（0，-3）；
②当点M在x轴上方时，同理可得点M（0，5），
同理可得，过点M且平行于AC的直线表达式为y=x+5③，
联立①③解得，
∴ Q的坐标为（4，9）；
综上，点Q的坐标为（0，-3）或（4，9）．

6.（1）设直线AB的解析式是y＝kx+b，
把点A（0，1），点B（3，0）代入得：解得：，
∴直线AB的解析式是：y＝﹣x+1；
（2）∵P（1，n），
∴D（1，），即PD＝n﹣，
∴S△ABP＝PD▪OB＝（n﹣）×3＝n﹣1；
（3）当S△ABP＝2时，2＝n﹣1，解得n＝2，
∴点P（1，2）．
∵E（1，0），
∴PE＝BE＝2，
∴∠EPB＝∠EBP＝45°
①如图1，∠CPB＝90°，BP＝PC，
过点C作CN⊥直线x＝1于点N．
∵∠CPB＝90°，∠EPB＝45°，
∴∠NPC＝∠EPB＝45°．
又∵∠CNP＝∠PEB＝90°，BP＝PC，
∴△CNP≌△BEP，
∴PN＝NC＝EB＝PE＝2，
∴NE＝NP+PE＝2+2＝4，
∴C（3，4）．
②如图2，∠PBC＝90°，BP＝BC，
过点C作CF⊥x轴于点F．
∵∠PBC＝90°，∠EBP＝45°，
∴∠CBF＝∠PBE＝45°．
又∵∠CFB＝∠PEB＝90°，BC＝BP，
∴△CBF≌△PBE．
∴BF＝CF＝PE＝EB＝2，
∴OF＝OB+BF＝3+2＝5，
∴C（5，2）．
③如图3，∠PCB＝90°，
∴∠CPB＝∠EBP＝45°，
∠CPB＝∠EBP，BP＝BP，∠PCB＝∠PEB＝90°
∴△PCB≌△BEP，
∴PC＝CB＝PE＝EB＝2，
∴C（3，2）．
∴以PB为边在第一象限作等腰直角三角形BPC，
综上所述点C的坐标是（3，4）或（5，2）或（3，2）．