初中数学北师大版八年级上册第六章 数据的分析4 数据的离散程度习题

这是一份初中数学北师大版八年级上册第六章 数据的分析4 数据的离散程度习题，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

6.4数据的离散程度

一、选择题
1. 一组数据2，3，2，3，5的方差是（ ）
A. 6 B. 3 C. 1.2 D. 2
2. 方差的计算公式s2＝[(x1－20)2＋(x2－20)2＋…＋(x9－20)2＋(x10－20)2]中，数字10和20分别表示的意义是( )
A. 数据的个数和方差 B. 数据的平均数和个数
C. 数据的个数和平均数 D. 数据的方差和平均数
3. 甲、乙两个样本，甲样本的方差是0.105，乙样本的方差是0.055，那么样本（ ）
A. 甲的波动比乙大 B. 乙的波动比甲大
C. 甲、乙的波动一样大 D. 甲、乙的波动无法确定

4．甲、乙、丙、丁四位同学五次数学测验成绩统计如下表，如果从这四位同学中，选出一位平均成绩较高且状态稳定的同学参加数学比赛，那么应选（  ）
人员
甲
乙
丙
丁
平均数
81
86
86
82
方差
40
45
55
59

A．甲 B．乙 C．丙 D．丁
5．为能很好地适应中考体育测试，某校九年级进行了3次体育模拟训练，甲、乙、丙三名同学成绩的平均分及方差如下表所示，那么这三名同学模拟训练成绩最稳定的是（    ）

甲
乙
丙

48
48
48

16
2
24

A．甲 B．乙 C．丙 D．无法确定
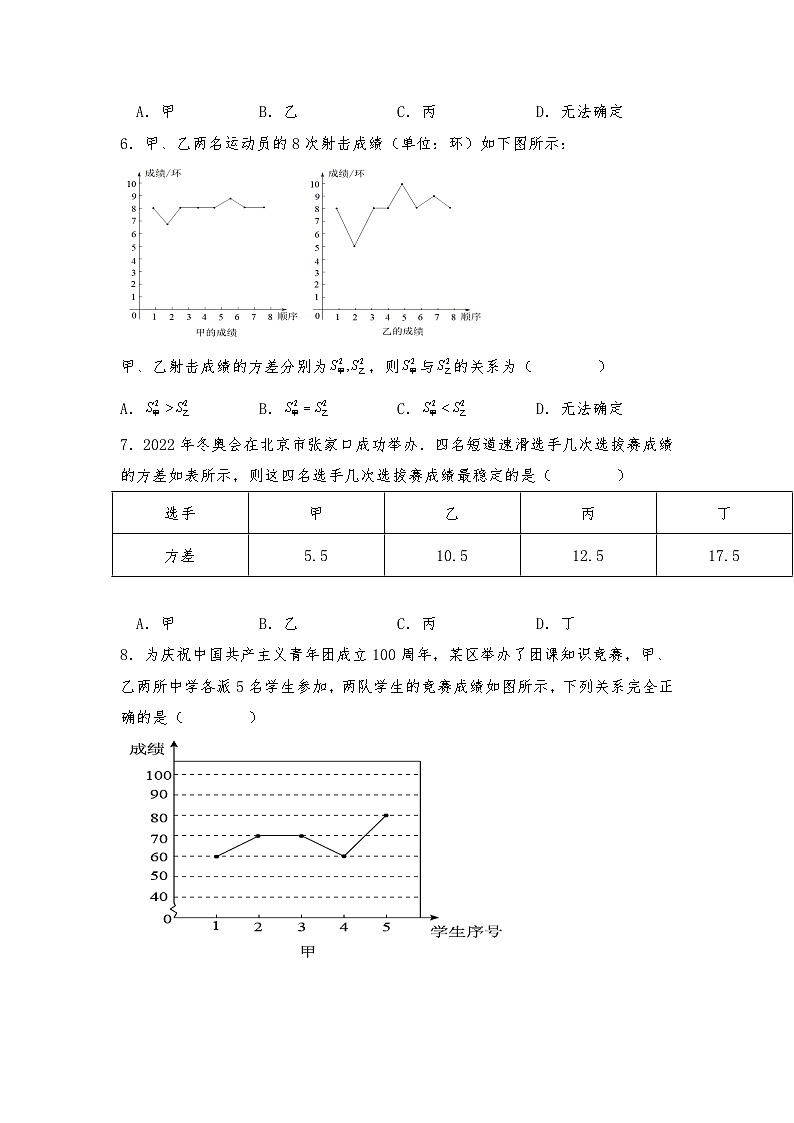
6．甲、乙两名运动员的8次射击成绩（单位：环）如下图所示：

甲、乙射击成绩的方差分别为，则与的关系为（    ）
A． B． C． D．无法确定
7．2022年冬奥会在北京市张家口成功举办．四名短道速滑选手几次选拔赛成绩的方差如表所示，则这四名选手几次选拔赛成绩最稳定的是（    ）
选手
甲
乙
丙
丁
方差
5.5
10.5
12.5
17.5

A．甲 B．乙 C．丙 D．丁
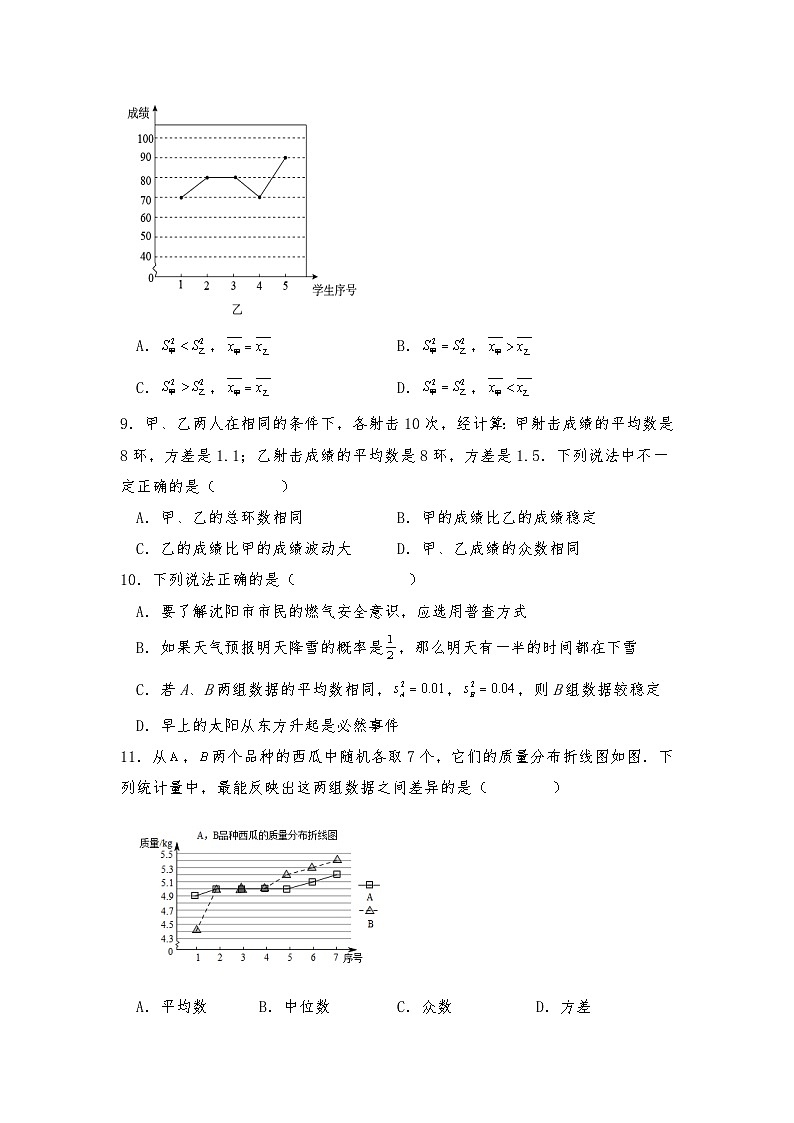
8．为庆祝中国共产主义青年团成立100周年，某区举办了团课知识竞赛，甲、乙两所中学各派5名学生参加，两队学生的竞赛成绩如图所示，下列关系完全正确的是（    ）

A．， B．，
C．， D．，
9．甲、乙两人在相同的条件下，各射击10次，经计算：甲射击成绩的平均数是8环，方差是1.1；乙射击成绩的平均数是8环，方差是1.5．下列说法中不一定正确的是（    ）
A．甲、乙的总环数相同 B．甲的成绩比乙的成绩稳定
C．乙的成绩比甲的成绩波动大 D．甲、乙成绩的众数相同
10．下列说法正确的是（       ）
A．要了解沈阳市市民的燃气安全意识，应选用普查方式
B．如果天气预报明天降雪的概率是，那么明天有一半的时间都在下雪
C．若A、B两组数据的平均数相同，，，则B组数据较稳定
D．早上的太阳从东方升起是必然事件
11．从，两个品种的西瓜中随机各取7个，它们的质量分布折线图如图．下列统计量中，最能反映出这两组数据之间差异的是（    ）

A．平均数 B．中位数 C．众数 D．方差
12．如图是根据南街米粉店今年6月1日至5日每天的用水量（单位：吨）绘制成的折线统计图．下列结论正确的是（　　）

A．平均数是6 B．众数是7 C．中位数是11 D．方差是8
13．已知样本，，，…，的方差是1，则样本，，，…，的方差是（    ）
A．1 B．2 C．3 D．4
14．颠球是练习足球球感最基本的招式之一某校足球队10名球员在一次训练中的颠球测试成绩（以“次”为单位计）为：52，50，46，54，50，56，47，52，53，50．则以下数据中计算错误的是（    ）
A．平均数为51 B．方差为8.4 C．中位数为53 D．众数为50
二、填空题
1．甲、乙两人进行飞镖比赛，每人投5次，所得平均环数相等，甲所得环数的方差为5，乙所得环数如下：2，6，5，8，4，那么成绩较稳定的是_______．（填“甲”或“乙”）

2．甲、乙两人在相同条件下进行射击练习，每人10次射击成绩的平均值都是7.5环，方差分别为，，则两人成绩比较稳定的是______（填“甲”或“乙”）．
3．农科院为某地选择甲、乙两种甜玉米种子时，甜玉米的产量和产量的稳定性是农科院所关心的问题，他们各用10块自然条件相同的试验田进行试验，下图是试验后得到的各试验田两种种子每公顷的产量（单位：t）．已知甲、乙两种甜玉米种子的平均产量相差不大，那么由样本估计总体，推测这个地区比较适合种植______（填“甲”或“乙”）种甜玉米，理由是_____________________．

4．已知一组数据：2，3，4，5，6，则这组数据的标准差是 __．
5．如果数据x1，x2，…，xn的方差是3，则另一组数据2x1，2x2，…，2xn的方差是_____．
6．若一组数据 3，4，5，x的极差是5，则x=______．
7．青少年科技创新大赛是一项具有30年历史的全国性青少年科技创新成果和科学探究项目的综合性科技竞赛．某校准备从甲、乙、丙、丁四个科创小组中选出一组参加青少年科技创新大赛．表格反映的是各组平时成绩的平均数（单位：分），及方差，如果要选出一个成绩较好且状态稳定的组去参赛，那么应去的组是________．

甲
乙
丙
丁

7
8
8
7

1
1.2
0.9
1.8


8．已知一个样本的方差S2[（6）2+（7）2+（8）2+（9）2]，求_____．

三、解答题

1．在全运会射击比赛的选拔赛中，运动员甲10次射击成绩的统计表和扇形统计图如下：
命中环数
10
9
8
7
命中次数

3
2



(1)根据统计表（图）中提供的信息，补全统计表及扇形统计图；
(2)已知乙运动员10次射击的平均成绩为9环，方差为1.2，如果只能选一人参加比赛，你认为应该派谁去？并说明理由．（参考资料：）







2．为弘扬民族精神，传播传统文化，某县教育系统将组织“弘扬传统文件化，永承华夏辉煌”的演讲比赛．某校各年级共推荐了19位同学参加初赛（校级演讲比赛），初赛成绩排名前10的同学进入决赛．
(1)若初赛结束后，每位同学的分数互不相同．某同学知道自己的分数后，要判断自己能否进入决赛，他只需知道这19位同学成绩的______；（填：平均数或众数或中位数）
(2)若初赛结束后，这19位同学的成绩如下：
签号
1
2
3
4
5
6
7
8
9
10
成绩
8.5
9.1
9.2
8.6
9.3
8.8
9.6
8.9
8.7
9.7
签号
11
12
13
14
15
16
17
18
19

成绩
9.8
9.1
8.9
9.3
9.6
8.8
9
8.7
9.3


2号选手笑着说：“我的成绩代表着咱们这19位同学的平均水平呀！”
14号选手说：“与我同分数的选手最多，我的成绩代表着咱们这19位选手的大众水平嘛！”
请问，这19位同学成绩的平均数为______，众数为______；
(3)已知10号选手与15号选手经常参加此类演讲比赛，她俩想看看近期谁的成绩较好、较稳定，她俩用近三次同时参加演讲比赛的成绩计算得到平均分一样，10号选手的方差为0.5，15号选手的方差为0.38．你认为______号选手的成绩比较稳定．








3．为了从甲、乙两位同学中选拔一人参加知识竞赛，举行了6次选拔赛，根据两位同学6次选拔赛的成绩，分别绘制了如图统计图．

(1)填写下列表格

平均数/分
中位数/分
众数/分
甲
90
①________
90
乙
②________
87.5
③________

(2)已求得甲同学6次成绩的方差为（），求出乙同学6次成绩的方差;
(3)你认为选择哪一位同学参加知识竞赛比较好？请说明理由．



















答案
一、选择题
C．C.A.B．B.C．A．D.D．D．D．D．D．C
二、填空题
1.乙．
2.乙．
3.甲；甲的产量比较稳定．
4.．
5.12
6.0或8．
7.丙．
8.7.5．
三、解答题
1.（1）
∵命中7环比例为10%，
∴命中7环的次数为10×10%=1，
∴命中10环的次数为10-（3+2+1）=4，
∴命中10环的比例为，命中8环的比例为，
将所求数据补充到统计表及扇形统计图中如下：
命中环数
10
9
8
7
命中次数
4
3
2
1


（2）
应该派甲去．
理由：（环）．
．
因为甲、乙两人的平均成绩相同，而，说明甲的成绩比乙的成绩稳定．所以应派甲去．
2.(1)
解：根据中位数即可判断自己是否进入决赛；
故答案为：中位数；
(2)
解：根据2号选手与14号选手所说的话，即可知道平均数为： ，众数为：，
故答案为：9.1，9.3；
(3)
解：10号选手的方差为0.5，15号选手的方差为0.38，
，
15号选手成绩比较稳定，
故答案为：15.
3.(1)
解：将甲的成绩从小到大排列，处在中间位置的两个数的平均数为＝91，
因此甲的中位数是91分；
乙的成绩的平均数为＝90（分），
乙的成绩的众数为85分
故答案为：91，90，85；
(2)
解：乙同学的方差是：
．
(3)
解：选择甲同学．
因为两人的平均数相同，说明两人实力相当，但甲的方差小于乙的方差，说明甲同学发挥更稳定，因此甲同学成绩更优秀，可以选择甲同学参加竞赛．