人教版九年级上册22.2二次函数与一元二次方程精品教学作业ppt课件

这是一份人教版九年级上册22.2二次函数与一元二次方程精品教学作业ppt课件，文件包含222二次函数与一元二次方程教学课件pptx、222二次函数与一元二次方程分层作业解析版docx、222二次函数与一元二次方程导学案解析版docx、222二次函数与一元二次方程教学设计docx、222二次函数与一元二次方程分层作业原卷版docx、222二次函数与一元二次方程导学案原卷版docx等6份课件配套教学资源，其中PPT共24页， 欢迎下载使用。

22.2 二次函数与一元二次方程
人教版数学九年级上册
学习目标1）二次函数与一元二次方程之间的联系。2）理解二次函数的图象与x轴交点的三种位置关系。3）利用二次函数的图象求一元二次方程的近似解 。重点理解二次函数与一元二次方程之间的联系。难点用图象求方程解的方法。
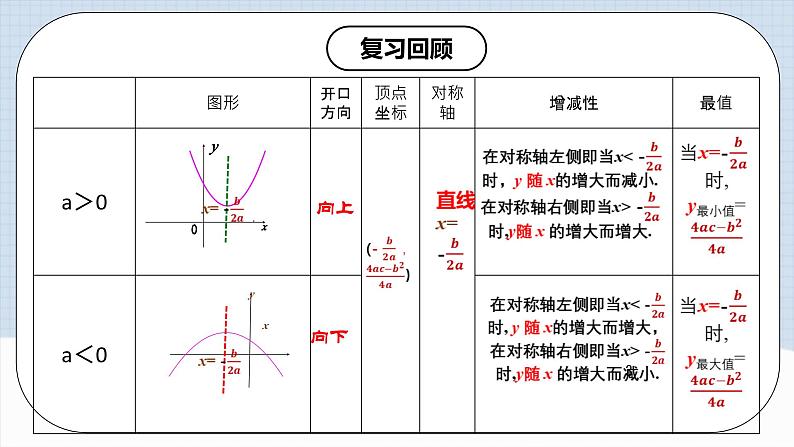
向上
向下
 
 
 
 
 
3
 
 
 
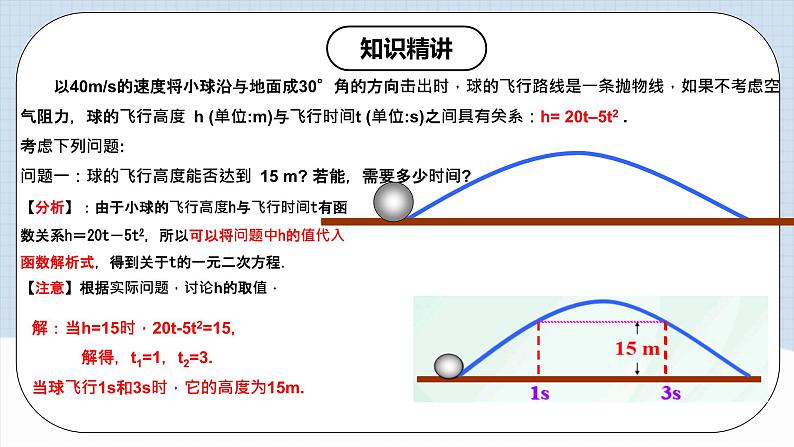
以40m/s的速度将小球沿与地面成30°角的方向击出时，球的飞行路线是一条抛物线，如果不考虑空气阻力，球的飞行高度 h (单位:m)与飞行时间t (单位:s)之间具有关系：h= 20t–5t2 . 考虑下列问题:问题一：球的飞行高度能否达到 15 m? 若能，需要多少时间?
【分析】：由于小球的飞行高度h与飞行时间t有函数关系h＝20t－5t2，所以可以将问题中h的值代入函数解析式，得到关于t的一元二次方程．【注意】根据实际问题，讨论h的取值．
解：当h=15时，20t-5t2=15， 解得，t1=1，t2=3.当球飞行1s和3s时，它的高度为15m.
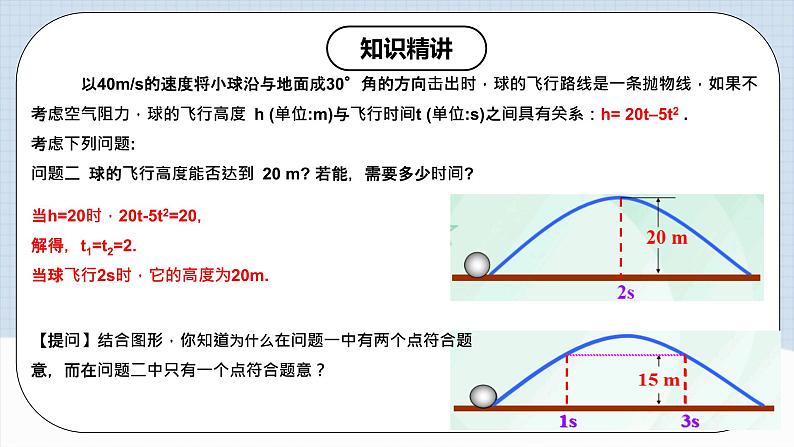
以40m/s的速度将小球沿与地面成30°角的方向击出时，球的飞行路线是一条抛物线，如果不考虑空气阻力，球的飞行高度 h (单位:m)与飞行时间t (单位:s)之间具有关系：h= 20t–5t2 . 考虑下列问题:问题二 球的飞行高度能否达到 20 m? 若能，需要多少时间?
当h=20时，20t-5t2=20， 解得，t1=t2=2.当球飞行2s时，它的高度为20m.
【提问】结合图形，你知道为什么在问题一中有两个点符合题意，而在问题二中只有一个点符合题意？
以40m/s的速度将小球沿与地面成30°角的方向击出时，球的飞行路线是一条抛物线，如果不考虑空气阻力，球的飞行高度 h (单位:m)与飞行时间t (单位:s)之间具有关系：h= 20t–5t2 . 考虑下列问题:问题三 球的飞行高度能否达到 20.5 m?为什么？
当h=20.5时，20t-5t2=20.5，化简得，t2-4t+4.1=0，因为（-4）2-4×4.1<0，所以方程无实根. 故球的飞行高度达不到20.5m.
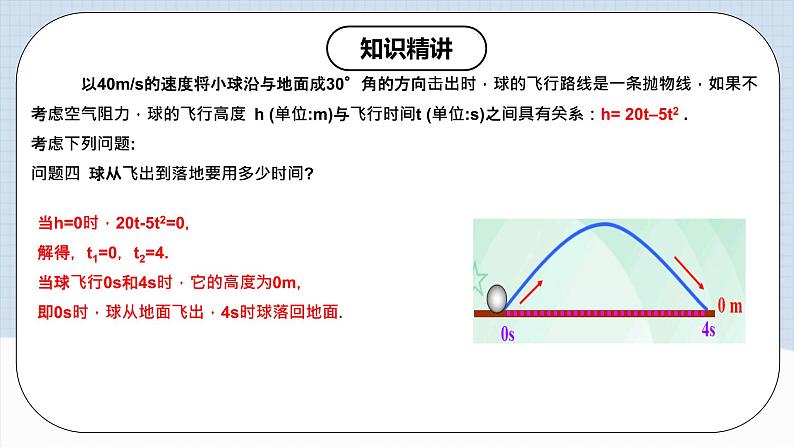
以40m/s的速度将小球沿与地面成30°角的方向击出时，球的飞行路线是一条抛物线，如果不考虑空气阻力，球的飞行高度 h (单位:m)与飞行时间t (单位:s)之间具有关系：h= 20t–5t2 . 考虑下列问题:问题四 球从飞出到落地要用多少时间?
当h=0时，20t-5t2=0，解得，t1=0，t2=4.当球飞行0s和4s时，它的高度为0m，即0s时，球从地面飞出，4s时球落回地面.
从上面发现，一般地，当 y 取定值且 a≠0 时，二次函数为一元二次方程。如：y=5 时，5=ax2+bx+c 就是一个一元二次方程。所以二次函数与一元二次方程关系密切。 例如：已知二次函数y=-x2+4x的值为3，求自变量x 的值。就是求方程3=-x2+4x(即x2-4x+3=0)的解。 反过来，解方程x2-4x+3=0，就是已知二次函数y=x2-4x+3的值为0，求自变量x的值。
 
解题技巧
1.画出下列二次函数图象1)y=x2+x-2；2)y=x2-6x+9；3)y=x2-x+1，2.你得出相应的一元二次方程的解吗?
6 5 4 3 2 1 -1 -2 -3 -4
6 5 4 3 2 1 -1 -2 -3 -4
y=x2+x-2
二次函数y=ax2+bx+c的图象和x轴交点的横坐标与一元二次方程ax2+bx+c=0的根有什么关系?
与x轴有两个不同的交点（x1，0）（x2，0）
与x轴没有交点
有两个不同的解x=x1，x=x2
没有实数根
有两个重合的公共点
有两个相等的实数根
P(2,-2)
P’(3,1)
重复上述过程，不断缩小根的范围，根所在两端的值就越来越接近根的值.因而可以作为根的近似值。
 
 
P(2,-2)
P’(3,1)
 
由上面的结论，我们可以利用二次函数的图象求一元二次方程的根。由于作图或观察可能存在误差，由图象求得的根，一般是近似的。
 
 
 
 
 
 
变式1-6 在图中画出函数y=x2-2x-3的图象，利用图象回答:(1)方程x2-2x-3=0的解是多少；(2) x取什么值时，函数值大于0；(3) x取什么值时，函数值小于0.
解：图象如图所示.(1) 方程x2-2x-3=0的解为x1=-1，x2=3.(2) x>3或x<-1时，函数值大于0.(3) -1典例2．根据下面表格中的对应值：
判断方程ax2＋bx＋c＝0(a≠0，a，b，c为常数)的一个解x的范围是(　　)A．3＜x＜3.23 B．3.23＜x＜3.24 C．3.24＜x＜3.25 D．3.25＜x＜3.26
【详解】解：函数y=ax2+bx+c的图象与x轴的交点就是方程ax2+bx+c=0的根，函数y=ax2+bx+c的图象与x轴的交点的纵坐标为0；由表中数据可知：y=0在y=-0.02与y=0.03之间，∴对应的x的值在3.24与3.25之间即3.24＜x＜3.25．故选C．
 
 
 
 
 
 
 
【详解】利用二次函数和一元二次方程的性质．由表格中的数据看出-0.01和0.02更接近于0，故x应取对应的范围．故选C．
二次函数与一元二次方程
二次函数与一元二次方程的关系
 
 
有两个交点
根据函数图象求一元二次方程的近似解
 
一个交点
无交点
有两个不相等的实数根
有两个相等的实数根
无实数根