人教版初中数学九年级上册《 第二十二章 二次函数（章末总结）》 课件+单元测试（含教师学生版）

这是一份人教版初中数学九年级上册《 第二十二章 二次函数（章末总结）》 课件+单元测试（含教师学生版），文件包含第二十二章二次函数章末总结复习课件pptx、第二十二章二次函数单元测试解析版docx、第二十二章二次函数单元测试原卷版docx等3份课件配套教学资源，其中PPT共42页， 欢迎下载使用。

第二十二章 二次函数（章末总结）
学习目标1）掌握二次函数的概念、形式、图像与性质，并能根据二次函数的图像与性质解决相关问题。2）掌握用待定系数法求抛物线的解析式及二次函数的实际应用。重点1）掌握二次函数的图像及其性质。2) 熟悉抛物线的顶点、对称轴的求法。难点1)深刻理解二次函数与一元二次方程的关系。2)会利用二次函数解决相应的应用题。
一般地，形如y=ax²+bx+c(其中a,b,c是常数，a≠0)的函数叫做二次函数。
二次函数的一般式 ：ax 2 + bx + c = y（a≠0）
二次项
一次项
常数项
二次项系数
一次项系数
为什么要强调a≠0？
1)当b＝0时， y＝ax2＋c 2)当c＝0时， y＝ax2＋bx 3)当b＝0，c＝0时， y＝ax2
二次函数的特殊形式：
1)等号左边是变量y，右边是关于自变量x的整式；2)a,b,c为常数，且a≠0 ；3)等式的右边最高次数为2 ，可以没有一次项和常数项，但不能没有二次项；4)自变量x的取值范围是任意实数。
判断二次函数的注意事项：
（0，0）
（0，0）
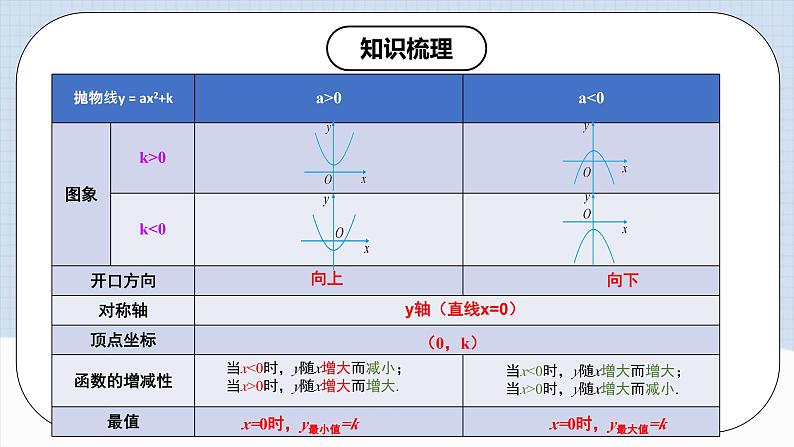
y轴
y轴
在x轴的上方（除顶点外）
在x轴的下方（除顶点外）
向上
向下
当x = 0时，最小值为0.
当x = 0时，最大值为0.
当x<0时，y随着x的增大而减小.当x>0时，y随着x的增大而增大.
当x<0时，y随着x的增大而增大.当x>0时，y随着x的增大而减小.
x=0时，y最小值=k
x=0时，y最大值=k
当x<0时，y随x增大而增大；当x>0时，y随x增大而减小.
当x<0时，y随x增大而减小；当x>0时，y随x增大而增大.
向上
向下
y轴（直线x=0）
（0，k）
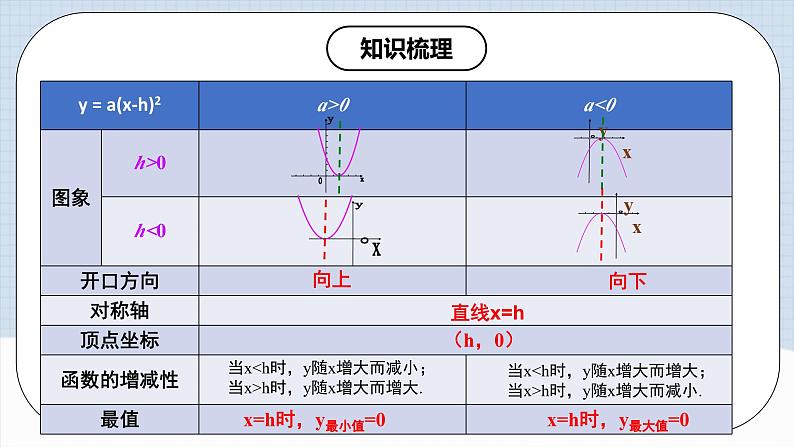
x=h时，y最小值=0
x=h时，y最大值=0
当xh时，y随x增大而减小.
当xh时，y随x增大而增大.
向上
向下
直线x=h
（h，0）
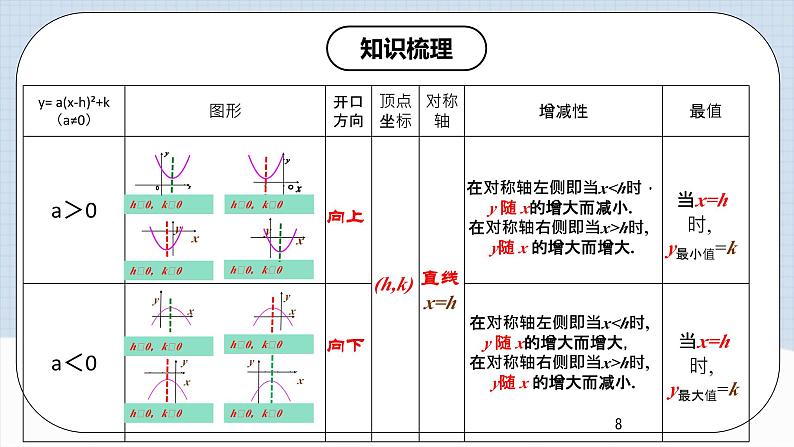
向上
向下
(h,k)
直线x=h
在对称轴左侧即当xh时, y随 x 的增大而增大.
在对称轴左侧即当xh时, y随 x 的增大而减小.
当x=h时,y最小值=k
当x=h时,y最大值=k
h﹥0，k﹥0
h﹤0，k﹥0
h﹤0，k﹤0
h﹥0，k﹤0
h﹥0，k﹥0
h﹤0，k﹥0
h﹤0，k﹤0
h﹥0，k﹤0
8
向上
向下
 
 
 
 
 
 
 
平移步骤：具体平移方法如下： 左右平移 上下平移 上下左右平移 上下平移 左右平移
⑴ 将抛物线解析式转化成顶点式y=a(x-h)²+k，确定其顶点坐标(h,k)；⑵ 保持抛物线y=ax²的形状不变，将其顶点平移到(h,k)处，
二次函数y=ax2+bx+c(a≠0)中1)当a>0时，抛物线开口向上，a的值越大，开口越小，反之，a的值越小，开口越大；2)当a<0时，抛物线开口向下，a的值越小，开口越小，反之，a的值越大，开口越大。【总结】a的正负决定开口方向，a的大小决定开口的大小(|a|越大，抛物线的开口小)．
y=2x2
y=x2
y=-2x2
y=-x2
 
二次函数y=ax2+bx+c(a≠0)中,c为常数项⑴ 当c>0时，抛物线与y轴的交点在x轴上方；⑵ 当c=0时，抛物线与y轴的交点为坐标原点；⑶ 当c<0时，抛物线与y轴的交点在x轴下方。【总结】c决定了抛物线与y轴交点的位置．
二次函数与一元二次方程
二次函数与一元二次方程的关系
 
 
有两个交点
根据函数图象求一元二次方程的近似解
 
一个交点
无交点
有两个不相等的实数根
有两个相等的实数根
无实数根
用二次函数解决实际问题的一般步骤：
1.审：仔细审题，厘清题意；2.设：找出题中的变量和常量，分析它们之间的关系，与图形相关的问题要结合图形具体分析，设出适当的未知数；3.列：用二次函数表示出变量和常量之间的关系，建立二次函数模型，写出二次函数的解析式；4.解：依据已知条件，借助二次函数的解析式、图象和性质等求解实际问题；5.检：检验结果，进行合理取舍，得出符合实际意义的结论.
 
 
2 下列二次函数中，二次项系数是﹣3的是（　　）A．y＝3x2﹣2x+5 B．y＝x2﹣3x+2 C．y＝﹣3x2﹣x D．y＝x2﹣3
3．（2020·利辛县九年级期中）已知y=（m+2）x|m|+2是关于x的二次函数，那么m的值为（　　）A．﹣2 B．2 C．±2 D．0
 
4 （2021·浙江杭州市·九年级期末）已知y关于 x的函数y=（m2+2m）x2+mx+m+1.1）当m为何值时，此函数是一次函数？ 2）当m为何值时，此函数是二次函数？
【详解】1）∵函数y=（m2+2m）x2+mx+m+1，是一次函数，∴m2+2m=0，m≠0， 解得：m=﹣2； 2）∵函数y=（m2+2m）x2+mx+m+1，是二次函数，∴m2+2m≠0，解得：m≠﹣2且m≠0．
5. 已知 a≠0，在同一坐标系中，y＝ax与y＝ax2的图象有可能是（ ）
【详解】解：A、函数y＝ax中，a＞0，y＝ax2中，a＞0，但当x＝1时，两函数图象有交点（1，a），故A错误；B、函数y＝ax中，a＜0，y＝ax2中，a＞0，故B错误；C、函数y＝ax中，a＜0，y＝ax2中，a＜0，但当x＝1时，两函数图象有交点（1，a），故C正确；D、函数y＝ax中，a＞0，y＝ax2中，a＜0，故D错误．故选：C．
6（2021·浙江绍兴市·九年级期中）已知抛物线y=-x2+1，下列结论：①抛物线开口向上；②抛物线与x轴交于点（-1，0）和点（1，0）；③抛物线的对称轴是y轴；④抛物线的顶点坐标是（0，1）；⑤抛物线y=-x2+1是由抛物线y=-x2向上平移1个单位得到的．其中正确的个数有（ ）A．5个 B．4个 C．3个 D．2个
 
7．（2021·甘肃平凉市·九年级期中）二次函数y＝x2＋1的图象大致是（ ）
【详解】解：二次函数y＝x2＋1中，a＝1＞0，图象开口向上，顶点坐标为（0，1），符合条件的图象是B．故选B．
8 下列关于二次函数y=x2﹣3的图象与性质的描述，不正确的是(　　)A．该函数图象的开口向上B．函数值y随着自变量x的值的增大而增大C．该函数图象关于y轴对称D．该函数图象可由函数y=x2的图象平移得到
【详解】A．由a=1＞0知抛物线开口向上，此选项描述正确；B．∵抛物线的开口向上且对称轴为y轴，∴当x＞0时，y随x的增大而证得：故此选项描述错误；由y=﹣x2+2x=﹣(x﹣1)2+1知抛物线的顶点坐标为(1，1)，此选项错误；C．∵抛物线的对称轴为y轴，∴该函数图象关于y轴对称，此选项描述正确；D．该函数图象可由函数y=x2的图象向下平移3个单位得到，此选项描述正确．故选：B．
 
 
【详解】在y=（x+1）2-2中由a=1＞0知抛物线的开口向上，故A错误；其对称轴为直线x=-1，在y轴的左侧，故B错误；由y=（x+1）2-2=x2+2x-1知抛物线与y轴的交点为（0，-1），在y轴的负半轴，故D错误；故选C．
 
 
【详解】y=（x+5）（x-3）=（x+1）2-16，顶点坐标是（-1，-16）． y=（x+3）（x-5）=（x-1）2-16，顶点坐标是（1，-16）．所以将抛物线y=（x+5）（x-3）向右平移2个单位长度得到抛物线y=（x+3）（x-5），故选B．
 
【详解】∵y=2x2+4x-1=2（x+1）2-3，∴当x=0时，y=-1，故选项A错误，该函数的对称轴是直线x=-1，故选项B错误，当x＜-1时，y随x的增大而减小，故选项C错误，当x=-1时，y取得最小值，此时y=-3，故选项D正确，故选D．
16 （河南省新乡市九年级期中）二次函数y=ax2+bx+c的图象如图所示，对称轴是x=－1．有以下结论：①abc>0，②4ac2，其中正确的结论的个数是（ ）A．1 B．2 C．3 D．4
【详解】①∵抛物线开口向下，∴a＜0，∵抛物线的对称轴为直线x=﹣1，∴b=2a＜0，∵抛物线与y轴的交点在x轴上方，∴c＞0，∴abc＞0，所以①正确；②∵抛物线与x轴有2个交点，∴△=b2-4ac＞0，∴4ac  
 
 
 
20（江苏常州市·九年级期末）二次函数y=ax2+bx+c的y与x的部分对应值如下表：则下列判断中正确的是（　　）A．抛物线开口向上 B．抛物线与y轴交于负半轴C．当x=﹣1时y＞0 D．方程ax2+bx+c=0的负根在0与﹣1之间
 
21 如图，某中学课外活动小组准备围建一个矩形苗圃园．其中一边靠墙，另外三边用长为20米的篱笆围成．已知墙长为18米，设这个苗圃园垂直于墙的一边的长为x米．(1)若这个苗圃园的面积为S平方米，求出S与x之间的函数关系式，并写出自变量x的取值范围；(2)垂直于墙的一边的长为多少米时，这个苗圃园的面积最大，并求出这个最大面积．
 
22 如图1，是抛物线形的拱桥，当拱顶高水面2米时，水面宽4米．如图建立平面直角坐标系，解答下列问题： (1)如图2，求该抛物线的函数解析式．(2)当水面AB下降1米，到CD处时，水面宽度增加多少米？（保留根号）(3)当水面AB上升1米时，水面宽度减少多少米？（保留根号）
 
23 某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销．据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本．(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式；(2)求出销售单价为多少元时，每天的销售利润最大？最大利润是多少？(3)如果该企业要使每天的销售利润不低于4000元，那么销售单价应控制在什么范围内？
【详解】解：（1）y=（x﹣50）[50+5（100﹣x）]=﹣5x2+800x﹣27500，∴y=﹣5x2+800x﹣27500（50≤x≤100）；（2）y=﹣5x2+800x﹣27500=﹣5（x﹣80）2+4500，∵a=﹣5＜0，∴抛物线开口向下．∵50≤x≤100，对称轴是直线x=80，∴当x=80时，y最大值=4500；（3）当y=4000时，﹣5（x﹣80）2+4500=4000，解得x1=70，x2=90．∴当70≤x≤90时，每天的销售利润不低于4000元．
24 如图，某足球运动员站在点O处练习射门，将足球从离地面0.5m的A处正对球门踢出(点A在y轴上)，足球的飞行高度y(单位：m)与飞行时间t(单位：s)之间满足函数关系y＝at2＋5t＋c，已知足球飞行0.8s时，离地面的高度为3.5m.(1)足球飞行的时间是多少时，足球离地面最高？最大高度是多少？(2)若足球飞行的水平距离x(单位：m)与飞行时间t(单位：s)之间具有函数关系x＝10t，已知球门的高度为2.44m，如果该运动员正对球门射门时，离球门的水平距离为28m，他能否将球直接射入球门？