




















- 人教版初中数学九年级上册《 第二十二章 二次函数(章末总结)》 课件+单元测试(含教师学生版) 课件 14 次下载
- 人教版初中数学九年级上册 23.1 《图形的旋转》 课件+教案+导学案+分层作业(含教师学生版和教学反思) 课件 8 次下载
- 人教版初中数学九年级上册 23.2 《中心对称(第二课时)》 课件+教案+导学案+分层作业(含教师学生版和教学反思) 课件 6 次下载
- 人教版初中数学九年级上册 23.2 《中心对称(第三课时)》 课件+教案+导学案+分层作业(含教师学生版和教学反思) 课件 6 次下载
- 人教版初中数学九年级上册 23.3 《课题学习 图案设计》 课件+教案+导学案+分层作业(含教师学生版和教学反思) 课件 5 次下载
初中数学人教版九年级上册23.2.1 中心对称公开课教学作业课件ppt
展开![]() 23.2 中心对称(第一课时)
23.2 中心对称(第一课时)
【A组-基础题】
1.(2020绍兴市中考)如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )

A.平行四边形→正方形→平行四边形→矩形
B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形→菱形→矩形
D.平行四边形→菱形→正方形→矩形
2.图中的两个梯形成中心对称,点P的对称点是( )

A.点A B.点B C.点C D.点D
3.如图,点O是▱ABCD的对称中心,EF是过点O的任意一条直线,它将平行四边形分成两部分,四边形ABFE和四边形EFCD的面积分别记为S1,S2,那么S1,S2之间的关系为( )
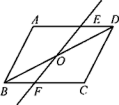
A.S1>S2 B.S1<S2 C.S1=S2 D.无法确定
4.如图,![]() 与
与![]() 关于
关于![]() 成中心对称,不一定成立的结论是( )
成中心对称,不一定成立的结论是( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.(2019湖州市中考)在数学拓展课上,小明发现:若一条直线经过平行四边形对角线的交点,则这条直线平分该平行四边形的面积. 如图是由5个边长为1的小正方形拼成的图形,![]() 是其中4个小正方形的公共顶点,小强在小明的启发下,将该图形沿着过点
是其中4个小正方形的公共顶点,小强在小明的启发下,将该图形沿着过点![]() 的某条直线剪一刀,把它剪成了面积相等的两部分,则剪痕的长度是( )
的某条直线剪一刀,把它剪成了面积相等的两部分,则剪痕的长度是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )

A.①② B.②③ C.①③ D.①②③
7.如图,已知长方形的长为10cm,宽为4cm,则图中阴影部分的面积为( )

A.20cm2 B.15cm2 C.10cm2 D.25cm2
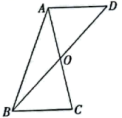
8.如图,已知点A与点C关于点O对称,点B与点D也关于点O对称,若![]() ,
,![]() .则AB的长可能是( )
.则AB的长可能是( )
A.3 B.4 C.7 D.11
9.请写出三个中心对称的汉字_______;请写出三个中心对称的字母______.
10.把直线 ![]() 绕原点旋转180°,所得直线的解析式为________.
绕原点旋转180°,所得直线的解析式为________.
11.如图所示,△ABC与△A'B'C'关于点O成中心对称,则下列结论成立的是__.(填序号)
①点A与点A'关于点O对称;②BO=B'O;③AC∥A'C';④∠ABC=∠C'A'B'.

12.如图,△ABC和△DEC关于点C成中心对称,若AC=1,AB=2,∠BAC=90°,则AE的长是_________.

13.如图,▱ABCD的周长为32cm,点O是▱ABCD的对称中心,AO=5cm,点E,F分别是AB,BC的中点,则△OEF的周长为_____cm.

14.如图,是4×4正方形网格,把其中一个标有数字的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形,则这个白色小正方形内的数字是_____.

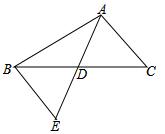
15.如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)图中哪两个图形成中心对称;
(2)若△ADC的面积为4,求△ABE的面积.
【B组-提高题】
16.(2018内江市中考)如图,在平面直角坐标系中,![]() 的顶点
的顶点![]() 在第一象限,点
在第一象限,点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,
,![]() ,
,![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() 与
与![]() 关于点
关于点![]() 成中心对称,则点
成中心对称,则点![]() 的坐标为( )
的坐标为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
17.如图,点O是![]() 的对称中心,
的对称中心,![]() ,E、F是
,E、F是![]() 边上的点,且
边上的点,且![]() ,G、H是
,G、H是![]() 边上的点,且
边上的点,且![]() ,若
,若![]() 分别表示
分别表示![]() 和
和![]() 的面积,则
的面积,则![]() 与
与![]() 之间的等量关系是( )
之间的等量关系是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
18.已知:如图,三角形ABM与三角形ACM关于直线AF成轴对称,三角形ABE与三角形DCE关于点E成中心对称,点E、D、M都在线段AF上,BM的延长线交CF于点P.
(1)求证:AC=CD;
(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.

数学23.2.1 中心对称示范课ppt课件: 这是一份数学<a href="/sx/tb_c88757_t3/?tag_id=26" target="_blank">23.2.1 中心对称示范课ppt课件</a>,文件包含2322中心对称图形pptx、中心对称mp4等2份课件配套教学资源,其中PPT共28页, 欢迎下载使用。
2020-2021学年23.2.1 中心对称教课课件ppt: 这是一份2020-2021学年23.2.1 中心对称教课课件ppt,共11页。
人教版九年级上册23.2.1 中心对称集体备课课件ppt: 这是一份人教版九年级上册23.2.1 中心对称集体备课课件ppt,共25页。PPT课件主要包含了21中心对称,第三步移开三角板,合作探究,试一试,中心对称,轴对称,灵活运用体会内涵,点A′即为所求的点,动手画一画,动手练一练等内容,欢迎下载使用。














