河北省石家庄市长安区2022-2023学年八年级下学期期末数学试卷（含答案）

这是一份河北省石家庄市长安区2022-2023学年八年级下学期期末数学试卷（含答案），共17页。试卷主要包含了选择题．，填空题，解答题等内容，欢迎下载使用。

1．（3分）如图，“心形”图片盖住的点的坐标可能是（ ）
A．（2，﹣4）B．（﹣4，2）C．（﹣1，﹣2）D．（﹣2，4）
2．（3分）如图，学校在琪琪家的（ ）
A．北偏东30°的方向上
B．北偏东30°的方向上，且距离琪琪家2km
C．南偏东60°的方向上，且距离琪琪家2km
D．北偏东60°的方向上，且距离琪琪家2km
3．（3分）函数y＝的自变量x的取值范围是（ ）
A．x≠0B．x≠1C．x≥1D．x≤1
4．（3分）某校为了解1500名学生周日晚上的睡眠时间，进行了问卷调查，从中抽取了100名学生的睡眠时间，下面说法不正确的是（ ）
A．1500名学生周日晚上的睡眠时间是总体
B．每名学生周日晚上的睡眠时间是个体
C．100名学生是所抽取的一个样本
D．样本的容量是100
5．（3分）如图是加油机上的数据显示牌，其中的变量是（ ）
A．金额B．单价C．油量D．金额和油量
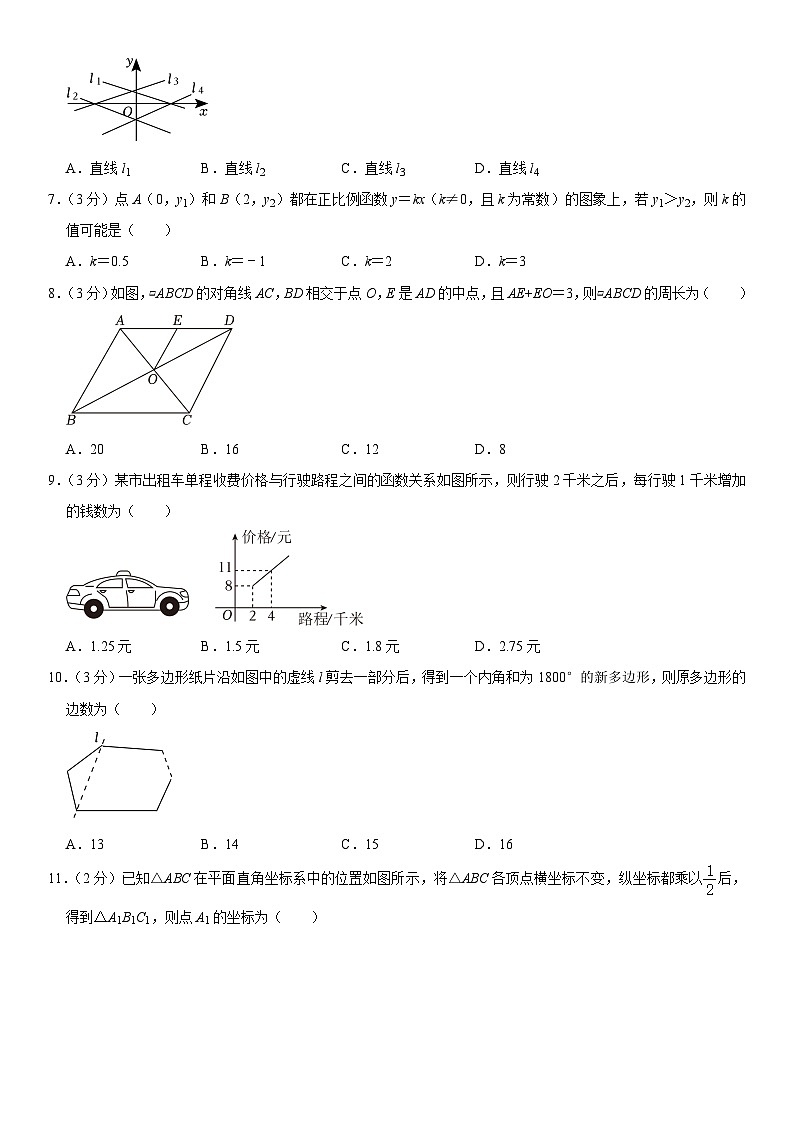
6．（3分）如图，在平面直角坐标系中，一次函数的图象可能是（ ）
A．直线l1B．直线l2C．直线l3D．直线l4
7．（3分）点A（0，y1）和B（2，y2）都在正比例函数y＝kx（k≠0，且k为常数）的图象上，若y1＞y2，则k的值可能是（ ）
A．k＝0.5B．k＝﹣1C．k＝2D．k＝3
8．（3分）如图，▱ABCD的对角线AC，BD相交于点O，E是AD的中点，且AE+EO＝3，则▱ABCD的周长为（ ）
A．20B．16C．12D．8
9．（3分）某市出租车单程收费价格与行驶路程之间的函数关系如图所示，则行驶2千米之后，每行驶1千米增加的钱数为（ ）
A．1.25元B．1.5元C．1.8元D．2.75元
10．（3分）一张多边形纸片沿如图中的虚线l剪去一部分后，得到一个内角和为1800°的新多边形，则原多边形的边数为（ ）
A．13B．14C．15D．16
11．（2分）已知△ABC在平面直角坐标系中的位置如图所示，将△ABC各顶点横坐标不变，纵坐标都乘以后，得到△A1B1C1，则点A1的坐标为（ ）
A．（﹣3，2）B．（﹣3，1）C．（﹣2，1）D．（﹣2，2）
12．（2分）如图，∠MON＝90°，在此基础上用尺规作出正方形AOBC，下面说法不正确的是（ ）
A．弧③的半径长等于弧①的半径长
B．弧②的半径长等于弧①的半径长
C．弧②的半径长小于弧①的半径长
D．弧②的半径长等于弧③的半径长
13．（2分）如图，矩形ABCD的对角线交于点O，以点O为原点建立平面直角坐标系，AC所在直线为y轴，AB＝2，，则点C的坐标为（ ）
A．（0，﹣2）B．（0，2）C．（0，﹣）D．（0，﹣1）
14．（2分）如图，点A（﹣1，3），B（2，2），若N是x轴上使得|NA﹣NB|的值最大的点，则ON的长为（ ）
A．B．C．8D．6
15．（2分）如图，四边形ABCD中，BD为对角线，AB＝2，CD＝2.8，E，F分别是边AD，BC的中点，则EF的取值范围是（ ）
A．0.4＜EF≤2.4B．0.4≤EF＜2.4C．0.8＜EF≤4.8D．0.8≤EF＜4.8
16．（2分）如图，在平面直角坐标系中，点A1（1，0），点A1第1次跳动至点A2（﹣1，1），第2次跳动至点A3（2，1），第3次跳动至点A4（﹣2，2），第4次跳动至点A5（3，2）…依此规律跳动下去，点A1第50次跳动至点A51的坐标是（ ）
A．（24，23）B．（25，25）C．（26，25）D．（27，26）
二、填空题（本大题共4个小题，每小题3分，共12分．第20小题第一空2分，第二空1分．把答案写在题中横线上）
17．（3分）点P（4，﹣3）关于x轴对称的点的坐标是 ．
18．（3分）如图，将点A（2，0）绕着原点O逆时针方向旋转120°得到点B，则点B的坐标是 ．
19．（3分）某市计划在生态公园内造一片有A，B两种树的混合林，需要购买这两种树苗共500棵，相关信息如表所示．设购买A种树苗x棵，造这片林的总费用为y元．则y（元）与x（棵）之间的函数表达式为 .（总费用＝购买树苗的费用+劳务费）
20．（3分）如图，正方形ABCD和正方形GBEF的边长分别是2和3，且点A，B，E在同一直线上，M是线段DF的中点，连结MG，MB，则MB的长为 ，MG的长为 ．
三、解答题（本大题共5个小题，共46分．解答应写出相应的文字说明或解题步骤）
21．（8分）已知点M（3a﹣6，a﹣1），根据下列条件分别求出点M的坐标．
（1）点M在y轴上；
（2）点N的坐标为（2，1）．直线MN∥y轴．
22．（8分）周末琪琪骑车郊游，当他骑了一段路时，发现所带饮用水不充足，于是又回到刚经过的某商店，买到水后继续去郊游的目的地，并在1.2小时到达目的地．如图是他本次郊游所用的时间与离家距离的关系示意图，根据图中提供的信息回答下列问题：
（1）琪琪家到郊游目的地的路程是 km，琪琪一共骑行了 km．
（2）在去目的地的途中，哪个时间段内琪琪的骑车速度最快？最快的速度是多少？
（3）如果琪琪到目的地后，琪琪因急事立刻以20km/h的速度回家，请在图中画出琪琪回家所用时间与离家距离的关系图象．
23．（9分）某校五四青年节期间举办了“青春飞扬”演讲比赛，将所有参赛选手的比赛成绩（得分均为整数）进行整理，并绘制成如图所示的扇形统计图和频数分布直方图．
（1）本次比赛参赛选手共有 人，扇形统计图中“79.5﹣89.5”这一范围的人数占总参赛人数的百分比为 ；
（2）补全图中的频数分布直方图；
（3）赛前规定，成绩由高到低，前40%的参赛选手获奖．某参赛选手的比赛成绩为86分，试判断他能否获奖，并说明理由．
24．（10分）如图，线段AB两个端点的坐标分别为A（﹣1，3），B（﹣1，1），直线l：y＝ax+b（a≠0，a，b为常数）经过点（3，0）和（﹣1，﹣4）．
（1）求直线l解析式；
（2）若将直线l向上平移n个单位长度，且平移后的直线经过线段AB的中点，求n的值；
（3）直线l1：y＝kx+m（k≠0）经过点C（1，0），且l1与线段AB有交点（包含A，B两点），直接写出k的取值范围．
25．（11分）【探究】如图1，正方形ABCD和正方形CEFG有公共顶点C．连接BG、DE．求证：BG＝DE．
【变式】如图2，菱形ABCD和菱形CEFG有公共顶点C，且∠A＝∠F、连接BG，DE．
（1）是否仍存在结论BG＝DE？若存在，给出证明，若不存在，请说明理由；
（2）如图3，当点G恰好落在对角线BD上时，点F在BD延长线上，且DF＝2DG，若△CED的面积为9，直接写出菱形ABCD的面积．
2022-2023学年河北省石家庄市长安区八年级（下）期末数学试卷
参考答案与试题解析
一、选择题（本大题共16个小题，1-10题每小题3分，11-16题每小题3分，共42分．在每小题给出的四个选项中，只有一项是符合题目要求的）．
1．【考点】点的坐标．
【分析】根据各象限内点的坐标特征解题，四个象限的符号特征为：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．
【解答】解：小手盖住的是第四象限的点，其点坐标特征为：横坐标为正数，纵坐标为负数，符合的只有A选项．
故选：A．
2．【考点】方向角．
【分析】根据题意可得：∠AOB＝90°，∠COB＝30°，然后利用角的和差关系可得∠AOC＝60°，再根据方向角的定义，即可解答．
【解答】解：如图：
由题意得：∠AOB＝90°，∠COB＝30°，
∴∠AOC＝∠AOB﹣∠COB＝60°，
∴学校在琪琪家的北偏东60°的方向上，且距离琪琪家2km，
故选：D．
3．【考点】函数自变量的取值范围．
【分析】根据分式有意义的条件是分母不为0，可得x﹣1≠0，解不等式即可．
【解答】解：根据题意，有x﹣1≠0，
解得x≠1．
故选：B．
4．【考点】总体、个体、样本、样本容量．
【分析】根据总体、个体、样本、样本容量的意义，逐一判断即可解答．
【解答】解：A、1500名学生周日晚上的睡眠时间是总体，正确，故A不符合题意；
B、每名学生周日晚上的睡眠时间是个体，正确，故B不符合题意；
C、100名学生是所抽取的一个样本，错误，应该是100名学生周日晚上的睡眠时间是所抽取的一个样本，故C符合题意；
D、样本的容量是100，正确，故D不符合题意；
故选：C．
5．【考点】常量与变量．
【分析】随着加油数量的增多，金额也增加，油量是自变量，金额是因变量．据此解答．
【解答】解：常量是固定不变的量，变量是变化的量，单价是不变的量，而金额是随着油量的变化而变化，所以其中的变量是金额和油量．
故选：D．
6．【考点】一次函数的图象．
【分析】根据一次函数的性质即可判断．
【解答】解：一次函数中，k＝﹣＜0，b＝1＞0，
∴一次函数过第一、二、四象限，
∴一次函数的图象可能是直线l1，
故选：A．
7．【考点】一次函数图象上点的坐标特征．
【分析】由当0＜2，y1＞y2，利用一次函数的性质可得出k＜0，即可得出结论．
【解答】解：∵0＜2，y1＞y2，
即y随x的增大而减小，
∴k＜0，
∴k值可以为﹣1．
故选：B．
8．【考点】平行四边形的性质；三角形中位线定理．
【分析】首先证明：OE＝BC，由AE+EO＝4，推出AB+BC＝8即可解决问题；
【解答】解：∵四边形ABCD是平行四边形，
∴OA＝OC，
∵AE＝ED，
∴OE＝CD，
∵AE+EO＝3，
∴2AE+2EO＝6，
∴AD+DC＝6，
∴平行四边形ABCD的周长＝2×6＝12，
故选：C．
9．【考点】一次函数的应用．
【分析】由题意可知，小数2千米是，收费为8元，行驶到4千米时，收费为11元，据此可得行驶2千米之后，每行驶1千米增加的钱数为1.5元．
【解答】解：由题意得：
（11﹣8）÷（4﹣2）＝1.5（元），
即行驶2千米之后，每行驶1千米增加的钱数为1.5元．
故选：B．
10．【考点】剪纸问题；多边形内角与外角．
【分析】根据多边形内角和公式，可得新多边形的边数，根据新多边形比原多边形少2条边，可得答案．
【解答】解：设新多边形是n边形，由多边形内角和公式得：
（n﹣2）×180°＝1800°，
解得n＝12，
原多边形的边数是12+2＝14．
故选：B．
11．【考点】坐标与图形性质．
【分析】首先根据点的位置得到点A的坐标，再将A点横坐标不变，纵坐标乘以即可得到点A1的坐标．
【解答】解：由图可知，A（﹣3，2），
∴点A1的坐标为（﹣3，1）．
故选：B．
12．【考点】作图—复杂作图；全等三角形的判定与性质；正方形的判定；正多边形和圆．
【分析】根据正方形的判定定理作图求解．
【解答】解：①以O为圆心，OA为半径作弧，交ON于B，
②分别以A，B为圆心，OA的长为半径作弧，两弧相交于C，
则四边形OACB为正方形，
故选：C．
13．【考点】矩形的性质；坐标与图形性质．
【分析】根据矩形的性质证明△OAB是等边三角形，得OA＝OB＝AB＝OC＝2，进而可得点C的坐标．
【解答】解：∵四边形ABCD是矩形，
∴OA＝OB＝OC＝OD，
∵∠ABD＝60°，
∴△OAB是等边三角形，
∴OA＝OB＝AB＝OC＝2，
∴点C的坐标为（0，﹣2），
故选：A．
14．【考点】轴对称﹣最短路线问题；坐标与图形性质．
【分析】连接AB并延长交x轴于N，由三角形第三边大于两边之差得，点N为所求，求出AB的关系式，再求出与x轴的交点即可．
【解答】解：连接AB并延长交x轴于N，由三角形第三边大于两边之差得，点N为所求，
∵A（﹣1，3），B（2，2），
∴AB：y＝﹣x+，
令y＝0，x＝8，
∴点N（8，0），
∴ON＝8，
故选：C．
15．【考点】三角形中位线定理．
【分析】取BD的中点H，连接EH、FH，根据三角形中位线定理分别求出EH、FH，根据三角形的三边关系解答即可．
【解答】解：取BD的中点H，连接EH、FH，
∵E、H分别为AD、BD的中点，
∴EH是△ABD的中位线，
∴EH＝AB＝1，
同理可得：FH＝CD＝1.4，
在△EHF中，FH﹣EH＜EF＜FH+EH，即0.4＜EF＜2.4，
当点H在EF上时，EF＝2.4，
∴0.4＜EF≤2.4，
故选：A．
16．【考点】规律型：点的坐标．
【分析】由图得，A3，A5，A7，…，A2n+1在第一象限，而A2，A4，A6，…，A2n在第二象限，判断出A51在第一象限，在依规律计算即可．
【解答】解：由图得，A3，A5，A7，…，A2n+1在第一象限，
而A2，A4，A6，…，A2n在第二象限，
∴A51在第一象限，
由A3（2，1）A5（3，2）A7（4，3）…，得，A2n+1（n+1，n），
∵2n+1＝51，
∴n＝25，
∴A2n+1（26，25）．
故选：C．
二、填空题（本大题共4个小题，每小题3分，共12分．第20小题第一空2分，第二空1分．把答案写在题中横线上）
17．【考点】关于x轴、y轴对称的点的坐标．
【分析】平面直角坐标系中任意一点P（x，y），关于x轴的对称点的坐标是（x，﹣y），记忆方法是结合平面直角坐标系的图形记忆，另一种记忆方法是记住：关于横轴的对称点，横坐标不变，纵坐标变成相反数．
【解答】解：点P（4，﹣3）关于x轴对称的点的坐标是（4，3）．
18．【考点】坐标与图形变化﹣旋转．
【分析】依据题意，在平面直角坐标系，确定B点的位置，再由特殊角的关系即可求出B的坐标．
【解答】解：点A（2，0）绕着原点O逆时针方向旋转120°得到点B，
∴B在第二象限．
如图，作BH⊥x轴于H．
∵∠BOA＝120°，
∴∠BOH＝60°．
∴∠OBH＝30°．
∴OH＝OB＝1，BH＝OB＝．
∴B（﹣1，）．故答案为：（﹣1，）．
19．【考点】一次函数的应用．
【分析】A种树苗为x棵时，B种树苗为（500﹣x）棵，A种树苗一棵总费用为（20+4）元，B种树苗一棵总费用为（25+5）元，根据题意容易写出函数关系式．
【解答】解：依题意，y＝（20+4）x+（25+5）（500﹣x），
即y＝﹣6x+15000．
故答案为：y＝﹣6x+15000．
20．【考点】正方形的性质；直角三角形斜边上的中线；勾股定理．
【分析】连接BD，BF，根据正方形的性质得到∠DBC＝∠CBF＝45°，求得∠DBF＝90°，得到BD＝2，BF＝3，根据勾股定理得到DF＝＝，根据直角三角形的性质得到BM＝DF＝，过M作MH⊥BG于H，根据全等三角形的性质得到∠BGM＝∠FGM＝45°，推出△GHM是等腰直角三角形，根据勾股定理即可得到结论．
【解答】解：连接BD，BF，
∵四边形ABCD，四边形BEFG是正方形，
∴∠DBC＝∠CBF＝45°，
∴∠DBF＝90°，
∵正方形ABCD和正方形GBEF的边长分别是2和3，
∴BD＝2，BF＝3，
∴DF＝＝，
∵M是线段DF的中点，
∴BM＝DF＝，
过M作MH⊥BG于H，
∵，
∴△BGM≌△FGM（SSS），
∴∠BGM＝∠FGM＝45°，
∴△GHM是等腰直角三角形，
∴MH＝GH，
∴BH＝3﹣HG，
∵BM2＝BH2+HM2，
∴，
∴HG＝1或HG＝5（不合题意舍去），
∴GM＝HG＝．
故答案为：，．
三、解答题（本大题共5个小题，共46分．解答应写出相应的文字说明或解题步骤）
21．【考点】坐标与图形性质．
【分析】（1）根据在y轴上点的坐标的横坐标为0，以此建立方程求解即可；
（2）根据MN∥y轴可知，点M，N的横坐标相等，以此建立方程求解即可．
【解答】解：（1）∵点M（3a﹣6，a﹣1）在y轴上，
∴3a﹣6＝0，
解得：a＝2，
则a﹣1＝1，
∴M（0，1）；
（2）∵直线MN∥y轴，
∴点M，N的横坐标相等，
∵M（3a﹣6，a﹣1），N（2，1）．
∴3a﹣6＝2，
解得：a＝，
则a﹣1＝，
∴M．
22．【考点】一次函数的应用．
【分析】（1）由图象直接可得琪琪家到郊游目的地的路程是12km，根据图象知，琪琪返回了2千米，即可求出一共骑行了16千米；
（2）分半列式算出各时间段的速度即可得到答案；
（3）求出回到家的时间t＝1.8，再画出图象即可．
【解答】解：（1）由图可得，琪琪家到郊游目的地的路程是12km，琪琪一共骑行了12+（6﹣4）×2＝16（km），
故答案为：12，16；
（2）当0≤x≤0.4时，琪琪的骑车速度是＝15（千米/小时），
当0.4＜x≤0.6时，琪琪的骑车速度是＝10（千米/小时），
当0.6＜x≤0.7时，琪琪的骑车速度是0（千米/小时），
当0.7＜x≤1.2时，琪琪的骑车速度是＝16（千米/小时），
∴0.7＜x≤1.2时，琪琪的骑车速度最快，最快的速度是16千米/小时；
（3）∵立刻以20km/h的速度回家，
∴回到家的时间为1.2+＝1.8，
画出图象如下：
23．【考点】频数（率）分布直方图；扇形统计图．
【分析】（1）根据两个统计图中，“89.5﹣99.5”的频数为8+4＝12人、所占调查人数的24%，由频率＝可求出调查人数；求出“59.5﹣69.5”所占的百分比，由各组频率之和为100%，可求出答案；
（2）求出“69.5﹣74.5”“79.5﹣84.5”的频数，即可补全频数分布直方图；
（3）求出成绩由高到低前40%的人数，调查相应的分数与86分比较即可．
【解答】解：（1）（8+4）÷24%＝50（人），
“59.5﹣69.5”所占的百分比为（2+1）÷50＝6%，
∴79.5﹣89.5”所占的百分比为1﹣6%﹣30%﹣24%＝40%，
故答案为：50，40%；
（2）样本中，“69.5﹣74.5”的人数为50×30%﹣8＝7（人），
“79.5﹣84.5”的人数为50×40%﹣8＝12（人），
补全频数分布直方图如下：
（3）能获奖．理由为：
获奖人数为50×40%＝20（人），
而“84.5﹣99.5”的人数为8+8+4＝20（人），
∴得分为86分的一定能获奖．
24．【考点】一次函数图象与几何变换；一次函数图象与系数的关系．
【分析】（1）利用待定系数法即可求得；
（2）根据平移的规律求得平移后的解析式，然后代入AB的中点坐标，即可求得n的值．
（3）把A，B的坐标代入求得k的值，然后根据图象即可求得．
【解答】解：（1）∵直线l：y＝ax+b（a≠0，a，b为常数）经过点（3，0）和（﹣1，﹣4），
∴，
解得，
∴直线l解析式为y＝x﹣3；
（2）由（1）知直线l的解析式为y＝x﹣3
∵A（﹣1，3），B（﹣1，1），
∴线段AB的中点为（﹣1，2），
设平移后的直线l的解析式为y＝x﹣3+n，
将线段AB的中点（﹣1，2）代入得2＝﹣1﹣3+n，
解得n＝6；
（3）∵直线l1：y＝kx+m（k≠0）经过点C（1，0），
∴k+m＝0，
∴m＝﹣k，
∴直线l1：y＝kx﹣k，
代入A（﹣1，3）得，3＝﹣k﹣k，解得k＝﹣，
代入A（﹣1，1）得，1＝﹣k﹣k，解得k＝﹣，
∴k的取值范围是﹣≤k≤﹣．
25．【考点】四边形综合题．
【分析】【探究】根据正方形的性质和同角的余角相等推出∠BCG＝∠DCE，推出判定△BCG≌△DCE发的条件后根据全等三角形的对应边相等即可推出结论；
【变式】（1）根据菱形的性质，结合已知条件推出∠BCD＝∠GCE，根据菱形四条边相等推出判定△BCG≌△DCE的条件，判定全等后再根据全等三角形的性质即可得出结论；
（2）先根据面积公式推出△DGC与△DEF的面积和等于△DCE的面积，再根据DF与DG之间的数量关系求出△DGC的面积，易得四边形DGCE的面积，然后根据△BCG≌△DCE推出△BCD的面积与四边形DGCE的面积，最后根据菱形的性质即可求出结果．
【解答】【探究】证明：∵四边形ABCD和四边形CEFG都是正方形，
∴CB＝CD，CG＝CE，∠BCD＝∠GCE＝90°，
∴∠BCG＝∠DCE，
在△BCG和△DCE中，
，
∴△BCG≌△DCE（SAS），
∴BG＝DE；
【变式】（1）存在．
证明：∵四边形ABCD和四边形CEFG都是菱形，
∴CB＝CD，CG＝CE，∠BCD＝∠A，∠F＝∠GCE，
又∵∠A＝∠F，
∴∠BCG＝∠DCE，
在△BCG和△DCE中，
，
∴△BCG≌△DCE（SAS），
∴BG＝DE；
（2）解：∵△DCE与菱形CEFG同底等高，
∴菱形CEFG的面积等于△DCE面积的2倍，
又∵△DCE的面积为9，
∴菱形CEFG的面积等于18，
∴S△DCG+S△DEF＝18﹣9＝9，
∵△DCG与△DEF中DG边与DF边上的高相等，
∴△DCG与△DEF的面积比等于DG与DF的比，
∵DF＝2DG，
∴S△DCG＝，
∴S△DCG＝3，S△DEF＝6，
∵△BCG≌△DCE，
∴S△BCG＝S△DCE＝9，
∴S△BCD＝9+3＝12，
∴菱形ABCD的面积＝12×2＝24．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2023/7/27 12:09:58
单价（元/棵）
劳务费（元/棵）
A种树苗
20
4
B种树苗
25
5