数学1.3 探索三角形全等的条件优质教案

这是一份数学1.3 探索三角形全等的条件优质教案，共3页。教案主要包含了知识与能力，过程与方法，情感态度价值观，教学重点，教学难点等内容，欢迎下载使用。
1.3探索三角形全等的条件（5）教学目标【知识与能力】掌握直角三角形全等的判定条件。【过程与方法】经历探索直角三角形全等条件的过程，掌握直角三角形全等的判定条件，并能运用其解决一些实际问题。【情感态度价值观】在几何推理中体会事物特殊与一般的关系，进而提高辩证思维能力.教学重难点【教学重点】 掌握三角形全等的“边边边”条件.【教学难点】   正确运用“边边边”条件判定三角形全等，解决实际问题.课前准备无教学过程一、知识回顾1.到目前为止，我们学习了几种三角形全等的判别方法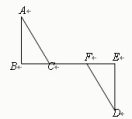？  2.如图，AB⊥BE于B，DE⊥BE于E，（1）若∠A=∠D，AB=DE，则△ABC与△DEF；根据.（2）若∠A=∠D，BC=EF，则△ABC与△DEF；根据.（3）若AB=DE，BC=EF，则△ABC与△DEF；根据. （4）若AB=DE，BC=EF，AC=DF则△ABC与△DEF；根据.  二、创设情境    我们已经学习了判定两个三角形全等的三个公理及一个推论：SAS、ASA、SSS、AAS。这几种判定方法中都有3个元素（其中至少有一条边）对应相等。我们知道，两个直角三角形有一对内角（直角）相等，判定两个直角三角形全等还需要几个条件？ 三、新知探索做一做：画一个Rt△ABC，使得∠C=90°，一直角边CA=4cm，斜边AB=5cm．把我们刚画好的直角三角形剪下来，和同桌的比比看，这些直角三角形有怎样的关系呢？  点拨：仿照课本P27的尺规作图。思考：你能证明吗？  三角形全等的条件5：斜边、直角边公理　斜边和一条直角边分别（对应）相等的两个直角三角形全等（可以简写成“斜边、直角边”或“HL”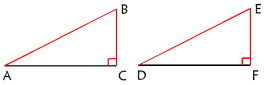）几何语言：在Rt△ABC和Rt△DEF中，∠C=∠F=90°    AB=DE    AC=DF∴Rt△ABC≌Rt△DEF（HL）。说明：明确“HL”是“Rt△”特有的判定两个三角形全等的方法，其他三角形没有，因此在证两个直角三角形全等时，书写必须明确“在Rt△***和Rt△***中，∠***=∠***=90°”。 四、例题评析例1．已知：如图，ABCD交于点O，AD=BC, ∠C=∠D=90°。求证：AO=BO,CO=DO。      变式：如例1图，∠C=∠D=90°。要证明△ABC≌△BAD、△AOC≌△BOD还需要什么条件？  例2．已知：如图，AB＝CD，DE⊥AC，BF⊥AC，E，F是垂足，AE＝CF。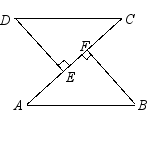（1）说明：△DEC≌△BFA  （2）．       拓展提高如图：AD是△ABC的高，E为AC上一点，BE交AD于F，且有BF=AC，FD=CD。（1）说明：△BDF≌△ADC（2）说明：BE⊥AC 。      五、课堂小结与反思1.用“HL”证两“Rt△”全等时，应注意书写格式。2.①两直角三角形两条直角边对应相等，这两个直角三角形全等，根据SAS。②两直角三角形斜边和一个锐角对应相等，这两个直角三角形全等，根据AAS。③两直角三角形一个锐角和一条直角边对应相等，这两个直角三角形全等，根据ASA或AAS。④两直角三角形全等的特殊条件是斜边和一条直角边对应相等。3．问题1：你能够用几种方法说明两个直角三角形全等？  问题2：谈谈“两条边对应相等的两个直角三角形全等”这句话的理解.