初中数学人教版七年级上册1.2.4 绝对值说课课件ppt

这是一份初中数学人教版七年级上册1.2.4 绝对值说课课件ppt，共25页。PPT课件主要包含了“形”，绝对值的几何意义，数结合，绝对值的代数意义，绝对值具有非负性，一日千里，二龙戏珠，三心二意，四面八方，五光十色等内容，欢迎下载使用。
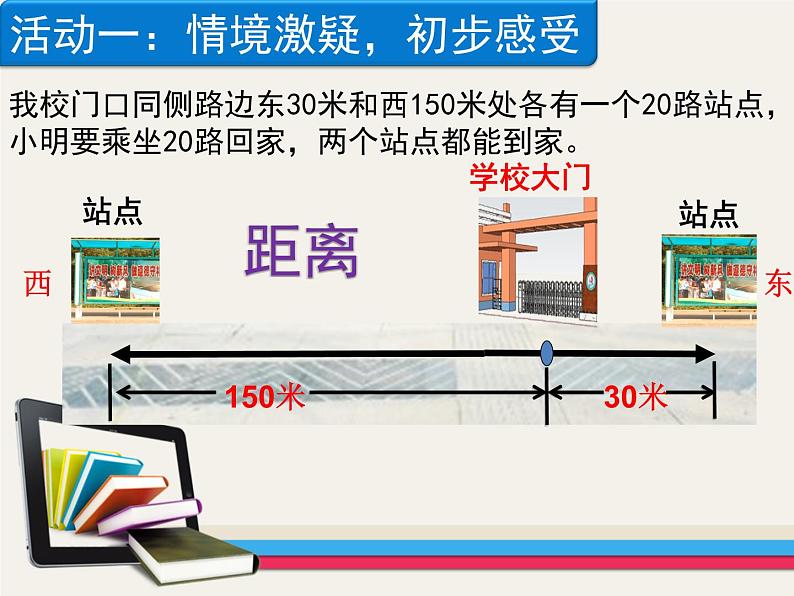
活动一：情境激疑，初步感受
我校门口同侧路边东30米和西150米处各有一个20路站点，小明要乘坐20路回家，两个站点都能到家。
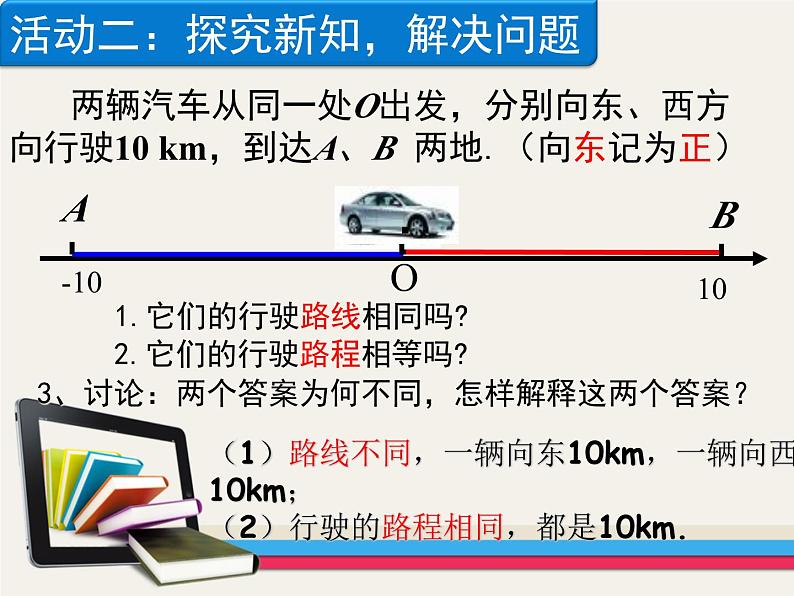
两辆汽车从同一处O出发，分别向东、西方向行驶10 km，到达A、B 两地.（向东记为正）
2.它们的行驶路程相等吗?
1.它们的行驶路线相同吗?
（1）路线不同，一辆向东10km，一辆向西10km； （2）行驶的路程相同，都是10km.
活动二：探究新知，解决问题
3、讨论：两个答案为何不同，怎样解释这两个答案？
1、绝对值的概念： 一般地，数轴上表示数a的点与原点的距离叫做数a的绝对值。
2、表示方法：数a的绝对值记作|a|。
3、想一想：数a可以表示什么样的数？
这里的数a可以是正数，负数和 0
A B
想一想 互为相反数的两个数的绝对值有什么关系？
一个数a的绝对值就是数轴上表示数a的点与原点的距离
互为相反数的两个数的绝对值相等
数轴上表示数a的点与原点的距离叫做数a的绝对值。
练习：1、在数轴上标出下列各点,再选几个你喜欢的点，并分别写出它们表示数的绝对值： 6，-0.5, 0, + ，-3
2、求值： = = = = = =
对于一个数的绝对值与这个数的关系，你有什么发现吗?试试分分类，将你的发现归纳。你还能再举例验证你的发现吗?
一个正数的绝对值是它本身；一个负数的绝对值是它的相反数； 0的绝对值是0。
如果a﹥0, 那么︱a︱= a 如果a﹦0，那么︱a︱= 0 如果a﹤0, 那么︱a︱= -a
写出下列各数的绝对值：3， -8，-3.9 ， ， ，100， 0
思考：1、什么数的绝对值是 5 ? 2、什么数的绝对值是 0 ? 3、是否存在绝对值是 -4 的数,为什么?
通过这三个问题的解答，你有什么发现？

活动三：挑战思维，形成能力
检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数,从轻重的角度看,最接近标准的是( )
活动四：例题解析，拓展能力
四个选项分别表示什么意思？“最接近标准”是什么意思？是哪个球？
你能利用绝对值说明一个有理数的意义吗？比如“-4”？
1.(教材变型题)若 ，则x＝_____；若 ，则x＝_____；若 ，则x＝_______.2.(易错题)化简 的结果为________3.(教材变型题)如果 ，则a的取值范围是 （ ）A、 B、 C、 D、4.(创新题)代数式 的最小值是（ ）A、0 B、2 C、3 D、55.(章节内知识点综合题)已知a、b为有理数，且 ， ， ，则 （ ）A、 B、C、 D、
本节课学习了哪些知识？
活动五：总结反思，方法归纳
一、（绝对值的意义） 1、绝对值的几何意义：在数轴上表示数a的点与_______的距离叫做数a的绝对值，记作_______. 2、绝对值的代数意义：一个正数的绝对值是____；一个负数的绝对值是_____；0的绝对值是_____.二、（绝对值的性质）（1）任何数都有绝对值，且只有_____个.（2）由绝对值的几何意义可知：距离不可能为负数，因此，任何一个数的绝对值都是_____数，绝对值最小的数是______.（3）绝对值是正数的数有___个，它们互为_____.（4）两个互为相反数的绝对值______；反之，绝对值相等的两个数______或________.
体会了哪些数学思想方法？
1.︱x︱=3,x= ； ︱y-3︱=0,则y= .
︱m︱=︱n︱,则m、n的关系是什么?
说出绝对值小于3的所有整数.
绝对值最小的数是 .
下列判断错误的是( ).A.一个正数的绝对值一定是正数 B.一个负数的绝对值一定是正数 C.任何数的绝对值一定是正数 D.任何数的绝对值都不是负数.
绝对值是4的数是（ ）.A.± 4 B.4 C.-4 D.2
判断：符号相反，绝对值相等的数互为相反数( ).