高中数学新教材选择性必修第二册课件+讲义 第4章 章末复习课

这是一份高中数学新教材选择性必修第二册课件+讲义 第4章 章末复习课，文件包含高中数学新教材选择性必修第二册第4章章末复习课pptx、高中数学新教材选择性必修第二册第4章章末复习课教师版docx、高中数学新教材选择性必修第二册第4章章末复习课学生版docx等3份课件配套教学资源，其中PPT共38页， 欢迎下载使用。

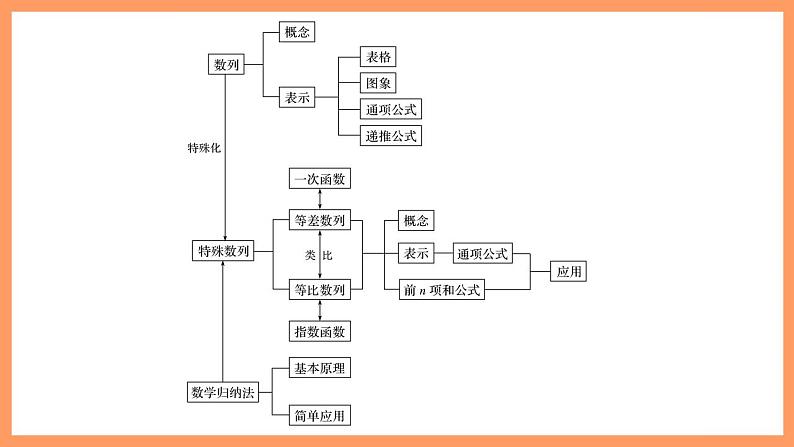
第4章 章末复习课高中数学新教材选择性必修第二册高考政策|高中“新”课程，新在哪里?1、科目变化：外语语种增加，体育与健康必修。第一，必修课程，由国家根据学生全面发展需要设置，所有学生必须全部修习、全部考试。第二，选择性必修课程，由国家根据学生个性发展和升学考试需要设置。第三，选修课程，由学校根据实际情况统筹规划开设，学生自主选择修习。2、课程类别变化，必修课程、选择性必修课程将成为高考考查范围。在毕业总学分不变的情况下，对原必修课程学分进行重构，由必修课程学分、选择性必修课程学分组成，适当增加选修课程学分。3、学时和学分变化，高中生全年假期缩减到11周。4、授课方式变化，选课制度将全面推开。5、考试方式变化，高考统考科目由教育部命题，学业水平合格性、等级性考试由各省命题。一、等差与等比数列的基本运算二、等差、等比数列的判定三、数列求和知识网络随堂演练知识网络一、等差与等比数列的基本运算1.数列的基本运算以小题居多，但也可作为解答题第一步命题，主要考查利用数列的通项公式及求和公式，求数列中的项、公差、公比及前n项和等，一般试题难度较小.2.通过等差、等比数列的基本运算，培养数学运算、逻辑推理等核心素养.例1　在等比数列{an}中，已知a1＝2，a4＝16.(1)求数列{an}的通项公式；解　设数列{an}的公比为q，由已知得16＝2q3，解得q＝2，所以an＝2×2n－1＝2n，n∈N*.(2)若a3，a5分别为等差数列{bn}的第3项和第5项，试求数列{bn}的通项公式及前n项和Sn.解　由(1)得a3＝8，a5＝32，则b3＝8，b5＝32.设数列{bn}的公差为d，所以bn＝－16＋12(n－1)＝12n－28，n∈N*.所以数列{bn}的前n项和反思感悟　在等差数列和等比数列的通项公式an与前n项和公式Sn中，共涉及五个量：a1，an，n，d或q，Sn，其中a1和d或q为基本量，“知三求二”是指将已知条件转换成关于a1，d或q，an，Sn，n的方程组，利用方程的思想求出需要的量，当然在求解中若能运用等差(比)数列的性质会更好，这样可以化繁为简，减少运算量，同时还要注意整体代入思想方法的运用.跟踪训练1　已知等差数列{an}的公差d＝1，前n项和为Sn.(1)若1，a1，a3成等比数列，求a1；解　因为数列{an}的公差d＝1，且1，a1，a3成等比数列，(2)在(1)的条件下，若a1＞0，求Sn.解　因为a1＞0，所以a1＝2，二、等差、等比数列的判定1.判断等差或等比数列是数列中的重点内容，经常在解答题中出现，对给定条件进行变形是解题的关键所在，经常利用此类方法构造等差或等比数列.2.通过等差、等比数列的判定与证明，培养逻辑推理、数学运算等核心素养.(1)求b1，b2，b3；将n＝1代入得，a2＝4a1，又a1＝1，所以a2＝4.将n＝2代入得，a3＝3a2，所以a3＝12.所以b1＝1，b2＝2，b3＝4.(2)判断数列{bn}是否为等比数列，并说明理由；解　{bn}是首项为1，公比为2的等比数列.理由如下：即bn＋1＝2bn，又b1＝1，所以{bn}是首项为1，公比为2的等比数列.(3)求数列{an}的通项公式.所以an＝n·2n－1，n∈N*.反思感悟　判断和证明数列是等差(比)数列的方法(1)定义法：对于n≥1的任意自然数，验证an＋1－an 为与正整数n无关的常数.(2)中项公式法：①若2an＝an－1＋an＋1(n∈N*，n≥2)，则{an}为等差数列. ②若a ＝an－1·an＋1(n∈N*，n≥2且an≠0)，则{an}为等比数列.(3)通项公式法：an＝kn＋b(k，b是常数)⇔{an}是等差数列；an＝c·qn(c，q为非零常数)⇔{an}是等比数列.(4)前n项和公式法：Sn＝An2＋Bn(A，B为常数，n∈N*)⇔{an}是等差数列；Sn＝Aqn－A(A，q为常数，且A≠0，q≠0，q≠1，n∈N*)⇔{an}是公比不为1的等比数列.证明　当n≥2时，两边同除以an－1an，(2)试问a1a2是否是数列{an}中的项？如果是，是第几项？如果不是，请说明理由.假设a1a2是数列{an}中的第t项，解得t＝11∈N*，所以a1a2是数列{an}中的第11项.三、数列求和1.数列求和一直是考查的热点，在命题中，多以与不等式的证明或求解相结合的形式出现.一般数列的求和，主要是将其转化为等差数列或等比数列的求和问题，题型多以解答题的形式出现，难度中等.2.通过数列求和，培养数学运算、逻辑推理等核心素养.例3　已知数列{an}是n次多项式f(x)＝a1x＋a2x2＋…＋anxn的系数，且f(1)＝ .(1)求数列{an}的通项公式；当n＝1时，a1＝1，S1＝1成立，所以an＝n(n∈N*).解　由(1)知f(x)＝x＋2x2＋…＋nxn，反思感悟　数列求和的常用类型(1)错位相减法：适用于各项由一个等差数列和一个等比数列对应项的乘积组成的数列.把Sn＝a1＋a2＋…＋an两边同乘以相应等比数列的公比q，得到qSn＝a1q＋a2q＋…＋anq，两式错位相减即可求出Sn.(2)裂项相消法：即将数列的通项分成两个式子的代数差的形式，然后通过累加抵消中间若干项的方法，裂项相消法适用于形如 (其中{an}是各项均不为零的等差数列，c为常数)的数列.(3)拆项分组法：把数列的每一项拆成两项(或多项)，再重新组合成两个(或多个)简单的数列，最后分别求和.(4)并项求和法：与拆项分组相反，并项求和是把数列的两项(或多项)组合在一起，重新构成一个数列再求和，一般适用于正负相间排列的数列求和，注意对数列项数(是奇数还是偶数)的讨论.(an－2n)(an＋1)＝0.由于{an}是正项数列，所以an＝2n，n∈N*.1.在等差数列{an}中，3(a3＋a5)＋2(a7＋a10＋a13)＝24，则该数列的前13项和为A.13 B.26 C.52 D.156解析　3(a3＋a5)＋2(a7＋a10＋a13)＝24，∴6a4＋6a10＝24，∴a4＋a10＝4，1234√1234√1234解析　设S奇＝a1＋a3＋…＋a15，S偶＝a2＋a4＋…＋a16，则有S偶－S奇＝(a2－a1)＋(a4－a3)＋…＋(a16－a15)＝8d，12343.已知{an}为等差数列，a1＋a3＋a5＝105，a2＋a4＋a6＝99，以Sn表示数列{an}的前n项和，则使得Sn取得最大值的n是A.21 B.20 C.19 D.18√1234解析　由a1＋a3＋a5＝105得，3a3＝105，∴a3＝35.同理可得a4＝33，∴d＝a4－a3＝－2，an＝a4＋(n－4)×(－2)＝41－2n.∴使Sn取得最大值的n是20.12344.记等比数列{an}的前n项积为Tn(n∈N*)，已知am－1am＋1－2am＝0，且T2m－1＝128，则m＝____.4又由am－1am＋1－2am＝0(am≠0)，得am＝2.则22m－1＝128，故m＝4.课程结束高中数学新教材选择性必修第二册