【核心素养目标】2.2《配方法解一元二次方程》课件+教案

这是一份【核心素养目标】2.2《配方法解一元二次方程》课件+教案，文件包含核心素养目标22《配方法解一元二次方程》课件pptx、核心素养目标22《配方法解一元二次方程》教案docx等2份课件配套教学资源，其中PPT共24页， 欢迎下载使用。
北师大版数学九年级上册
2.2 配方法解一元二次方程
教学目标
1.经历配方法解一元二次方程的过程，获得解二元一次方程的基本技能.2.经历用配方法解二次项系数不为1的一元二次方程的过程，体会其中的化归思想.3.能利用一元二次方程解决有关的实际问题，能根据具体问题的实际意义检验结果的合理性，进一步培养分析问题、解决问题的意识和能力.
复习导入
1、如果一个数的平方等于9，则这个数是 ， 若一个数的平方等于7，则这个数是 。 一个正数有几个平方根，它们具有怎样的关系？ 2、用字母表示因式分解的完全平方公式。
±3
 
一个正数有两个平方根，它们互为相反数
 
新知讲解
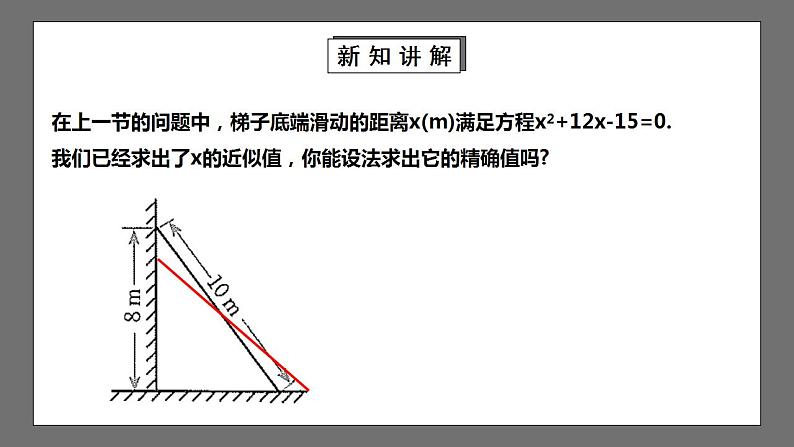
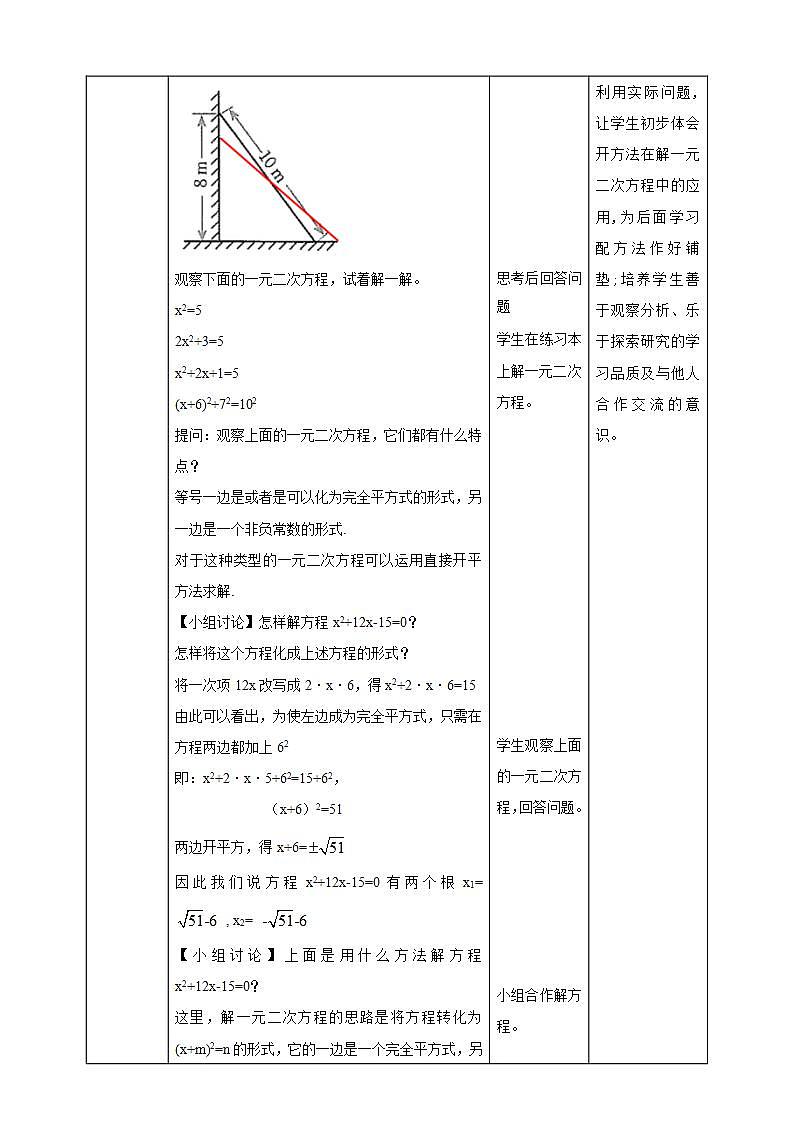
在上一节的问题中，梯子底端滑动的距离x(m)满足方程x2+12x-15=0.我们已经求出了x的近似值，你能设法求出它的精确值吗?
新知讲解
你会解下列一元二次方程吗？ 1.x2=5 2. 2x2+3=5 3.x2+2x+1=5 4.(x+6)2+72=102
 
(2)方程可化为x2=1，所以x1=1 , x2=-1.
 
 
观察这些方程都有什么特点？
新知讲解
等号一边是或者是可以化为完全平方式的形式，另一边是一个非负常数的形式.
对于这种类型的一元二次方程可以运用直接开平方法求解.
方程的特点
左边是完全平方式
右边是非负数
方程的形式： x2 = a (a≥0) 或 (mx+n) 2 = a (a≥0)
新知讲解
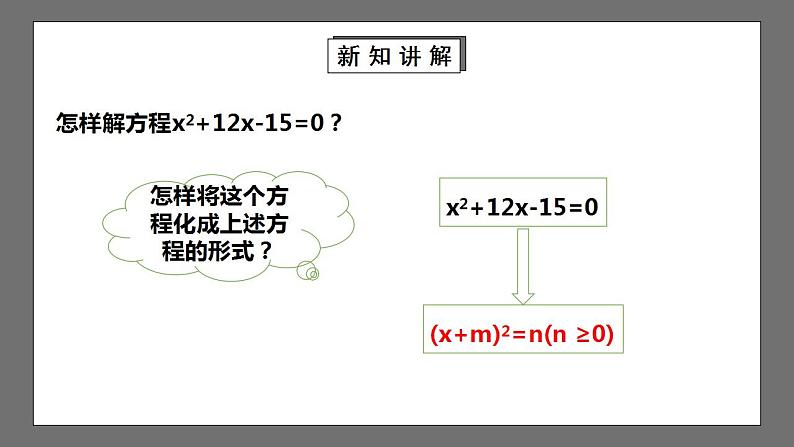
怎样解方程x2+12x-15=0？
怎样将这个方程化成上述方程的形式？
x2+12x-15=0
(x+m)2=n(n ≥0)
新知讲解
方位角和距离
将一次项12x改写成2·x·6，得x2+2·x·6=15
由此可以看出，为使左边成为完全平方式，只需在方程两边都加上62
即：x2+2·x·6+62=15+62， （x+6）2=51
 
 
x2+12x-15=0？
新知讲解
注意：解一元二次方程的思路是将方程转化为(x+m)2=n的形式，它的一边是一个完全平方式，另一边是一个常数，当n≥0时，两边同时开平方，转化为一元一次方程，便可求出它的根.
做一做
（1）x2 +12x + _____ = ( x + 6 )2　;（2）x2 - 4x + _____ = ( x - ____ )2　;（3）x2 + 8 x + ____ = ( x + ____ )2 .
36
4
2
4
上面等式的左边常数项和一次项系数有什么关系？
16
等式左边常数项是一次项系数的一半的平方.
对于形如 x2+ax 的式子如何配成完全平方式？
 
典例精析
例1、解方程x2+8x－9=0
解：移项，得x2+8x=9，
配方，得x2+8x+16=9+16，即 (x+4)2=25.
两边开平方，得x+4=±5，即 x+4=5 或 x+4=－5.∴x1=1，x2=－9.
我们通过配成完全平方式的方法得到了一元二次方程的根，这种解一元二次方程的方法称为配方法。
归纳总结
利用配方法解一元二次方程的步骤：
（1）移项:把常数项移到方程的右边;（2）配方:方程两边都加上一次项系数一半的平方;（3）变形:方程左边写成完全平方式,右边合并同类项;（4）开方：根据平方根的概念，将一元二次方程转化为两个一元一次方程；（5）求解：解一元一次方程；（6）定解：写出原方程的解．
新知讲解
观察下面两个一元二次方程的联系和区别： ① x2+8x－9=0; ② 3x2 +8x -3 = 0.
想一想怎么来解3x2 +8x -3 = 0.
典例精析
例2、解方程3x2+8x－3=0
 
 
 
 
 
在使用配方法过程中若二次项的系数不为1时，需要将二次项系数化为1后，再根据配方法步骤进行求解.
做一做
一个小球从地面以15m/s的初速度竖直向上弹出，它在空中的高度h (m)与时间 t (s)满足关系：h=15t - 5t2. 小球何时能达到10m高？
解：将 h = 10代入方程式中，得15t - 5t2 =10
两边同时除以-5，得 t2 - 3t = -2
 
 
所以在1s或2s时，小球可达10m高.
课堂练习
1. 用直接开平方法解下列一元二次方程，其中无实数根的方程为( )x2－1=0 B. x2=0 C. x2+4=0 D. －x2+3=02.一元二次方程x2－6x－6=0配方后化为( )A. (x－3)2=15 B. (x－3)2=3C. (x+3)2=15 D. (x+3)2=3
C
A
课堂练习
3. 若将方程x2+6x=7化为(x+m)2=16,则m= .
3
4.补全解方程2x2－4x－6＝0的过程．移项，得____________________，二次项系数化为1，得____________________，配方，得____________________，整理，得____________________，开平方，得____________________，解得x1＝________，x2＝________．
2x2－4x＝6
x2－2x＝3
x2－2x＋12＝3＋12
(x－1)2＝4
x－1＝±2
3
－1
课堂练习
 
 
课堂练习
 
(4)移项，得(1+x)2+2(1+x)=3.配方，得(1+x)2+2(1+x)+12=3+12.∴(1+x+1)2=4. ∴ x1=0，x2=－4.
巧将1+x看作整体进行配方，可达到简化的效果.
课堂练习
 
 
 
x=2，y=-3，z=2
 
课堂总结
配方法
方法
步骤
 
应用
求代数式的最值或证明
 
板书设计
一、配方法定义二、直接开平方法三、配方法解二元一次方程的步骤
课题：2.2 用配方法解二元一次方程
作业布置
教材第40页习题2.4 第1、2、3题
课程结束
北师大版数学九年级上册