【核心素养目标】2.5《一元二次方程根与系数的关系》课件+教案

这是一份【核心素养目标】2.5《一元二次方程根与系数的关系》课件，文件包含核心素养目标25《一元二次方程根与系数的关系》课件pptx、核心素养目标25《一元二次方程根与系数的关系》教案docx等2份课件配套教学资源，其中PPT共21页， 欢迎下载使用。

北师大版数学九年级上册
2.5 一元二次方程根与系数的关系
教学目标
1．掌握一元二次方程两根的和、两根的积与系数的关系．2．能根据根与系数的关系式和已知一个根的条件下，求出方程的另一根，以及方程中的未知系数．3．会利用根与系数的关系求关于两根代数式的值．
温故知新
 
想一想：一元二次方程的一般形式是怎样的？
你知道它的求根公式是什么吗？
ax2 + bx + c = 0 ( a≠0 )
适用的条件：Δ=b2-4ac≥0

当Δ＞0，Δ=0，Δ＜0 根的情况如何？
Δ > 0 时，方程有两个不相等的实数根；
Δ = 0 时，方程有两个相等的实数根；
Δ< 0 时，方程没有实数根.
新知讲解
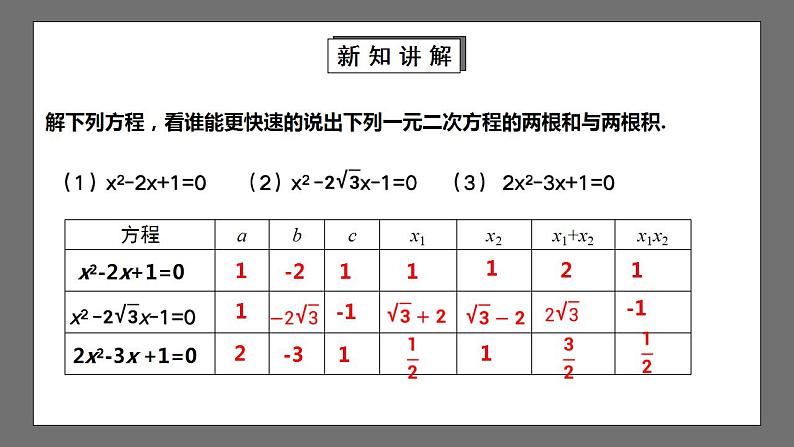
解下列方程，看谁能更快速的说出下列一元二次方程的两根和与两根积. 
 
x2-2x+1=0
 
2x2-3x +1=0
1
1
2
1
-1
1
1
-2
1
1
-1
2
-3
1
 
 
 
 
 
 
 
新知讲解
思考：对于任何一个一元二次方程，这种关系都成立吗？
新知讲解
证一证：
新知讲解
归纳总结
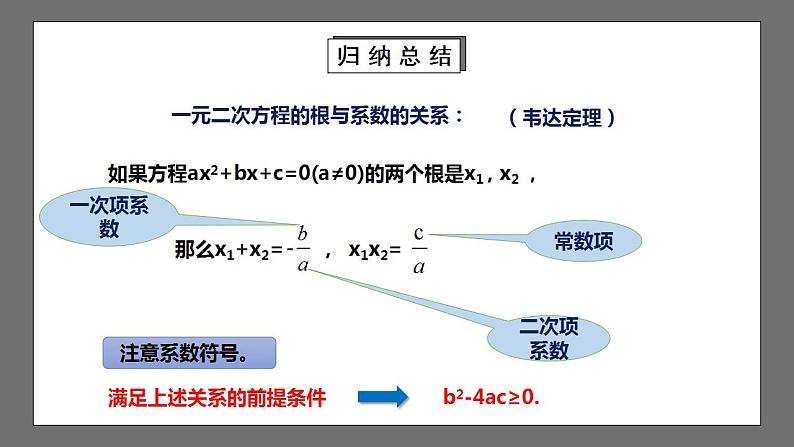
一元二次方程的根与系数的关系：
如果方程ax2+bx+c=0(a≠0)的两个根是x1 , x2 ,
那么x1+x2= , x1x2=
（韦达定理）
常数项
一次项系数
二次项系数
注意系数符号。
满足上述关系的前提条件
b2-4ac≥0.
典例精析
例1.利用根与系数的关系，求下列方程的两根之和、两根之积：(1)x2＋7x＋6＝0； (2)2x2－3x－2＝0.
解：(1)这里a＝1，b＝7，c＝6.Δ＝b2－4ac＝72－4×1×6＝49－24＝25>0.∴方程有两个实数根．设方程的两个实数根是x1，x2，那么x1＋x2＝－7，x1x2＝6.
典例精析
例1.利用根与系数的关系，求下列方程的两根之和、两根之积：(1)x2＋7x＋6＝0； (2)2x2－3x－2＝0.
 
新知讲解
想一想：应用根与系数的关系需注意什么？
练一练
 
4
1
14
12
求与方程的根有关的代数式的值时，一般先将所求的代数式化成含两根之和，两根之积的形式，再整体代入.
归纳总结
 
常见的涉及一元二次方程两根的代数式的重要变形:
课堂练习
1.设一元二次方程x2－6x＋4＝0的两实根分别为x1和x2，则(x1＋x2)－x1· x2 ＝(　　)A．－10　　　B．10　　　C．2　　　D．－22.已知一元二次方程x2－6x＋c＝0有一个根为2，则另一个根为(　　)A．2　　　　B．3　　　　C．4　　　　D．8
C
C
课堂练习
3．菱形的两条对角线长分别是方程x2－14x＋48＝0的两实根，则菱形的面积为____．
24
4．设a，b是方程x2＋x－2016＝0的两个不相等的实数根，则a2＋2a＋b的值为________．
2015
课堂练习
5.已知方程 5x2+kx-6 = 0 的一个根是 2，求它的另一个根及k 的值.
 
 
∵其中一个根为2，因此可以设 x1= 2，
 
课堂练习
6.如果一个三角形两边的长分别等于一元二次方程x2-17x+66=0的两个实数根，那么这个三角形的第三边的长可能是20吗？为什么？
解：由题意，可得 x1+x2 = 17，即两边长之和为 17，17小于 20，所以这个三角形的第三边的长不可能是 20.
课堂总结
①方程必须是一元二次方程的一般形式；②判断b2-4ac≥0；③使用x1+x2 时， 注意“－ ”不要漏写.
一元二次方程的根与系数的关系
根与系数的关系：
x1+x2 = ，
x1x2 =
注意事项：
板书设计
课题：2.5 一元二次方程根与系数的关系
一元二次方程 ax2 + bx + c = 0 (a ≠ 0，b2 – 4ac ≥ 0)的根与系数的关系：
作业布置
教材第51页习题2.8第1、3、4题
课程结束
北师大版数学九年级上册