人教版九年级上册22.2二次函数与一元二次方程精品ppt课件

这是一份人教版九年级上册22.2二次函数与一元二次方程精品ppt课件，共32页。PPT课件主要包含了y2x－4，从形的角度看，从数的角度看，t－220，∴方程没有实根，x2＋x－20，x21，yx2＋x－2，－20，x2－x＋10等内容，欢迎下载使用。

二次函数与一元二次方程的联系再次展示了函数与方程的联系，一方面可以深化对一元二次方程的认识，另一方面又可以运用二次函数解决一元二次方程的有关问题．
学习目标： 了解二次函数与一元二次方程的联系.学习重点： 二次函数与一元二次方程的联系．
一次函数y=kx＋b (k≠0)的图象与x轴的交点的坐标与一元一次方程kx＋b=0的根有什么关系？
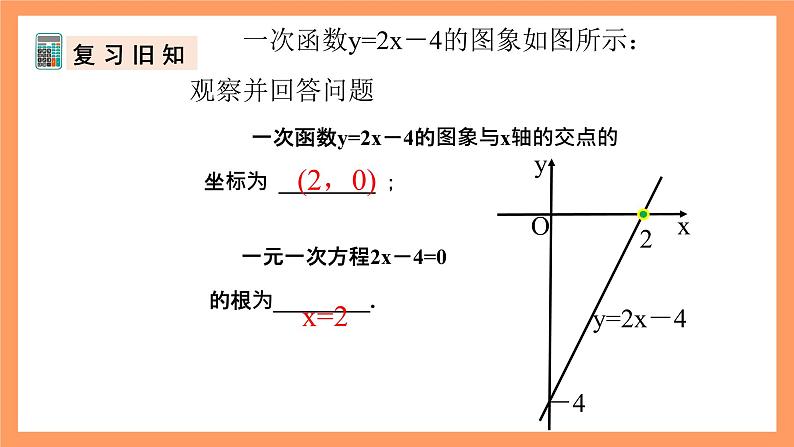
一次函数y=2x－4的图象与x轴的交点的坐标为 _________ ； 一元一次方程2x－4=0 的根为_________.
一次函数y=2x－4的图象如图所示：观察并回答问题
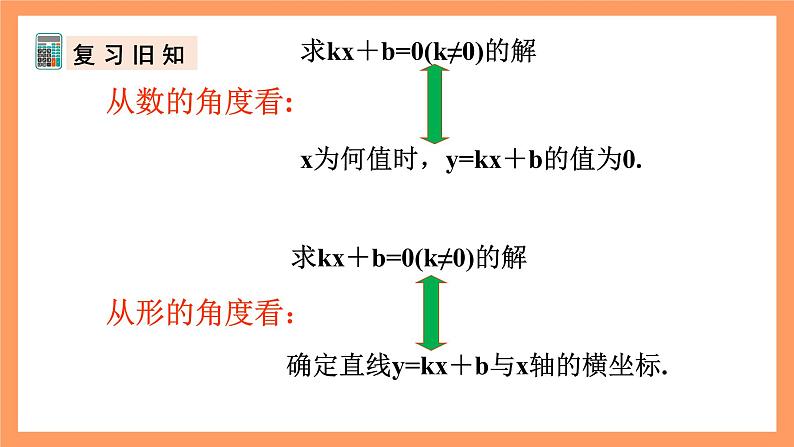
求kx＋b=0(k≠0)的解
x为何值时，y=kx＋b的值为0.
确定直线y=kx＋b与x轴的横坐标.
通过观察对比，一次函数y=kx＋b (k≠0)的图象与x轴的交点的坐标与一元一次方程kx＋b=0的根有什么关系？
结论：一次函数y=kx＋b(k≠0)的图象与x轴的交点的横坐标就是一元一次方程kx＋b=0(k≠0)的根.
二次函数y=ax2＋bx＋c(a≠0)的图象和x轴交点的横坐标与一元二次方程ax2＋bx＋c=0(a≠0)的根有什么关系?
以 40 m /s的速度将小球沿与地面成 30°角的方向击出时,球的飞行路线是一条抛物线，如果不考虑空气阻力，小球的飞行高度 h(单位:m)与飞行时间 t(单位:s)之间具有函数关系： h= 20t－5t2 考虑下列问题: (1)球的飞行高度能否达到 15 m? 若能，需要多少时间? (2)球的飞行高度能否达到 20 m? 若能，需要多少时间? (3)球的飞行高度能否达到 20.5 m?为什么？ (4)球从飞出到落地要用多少时间?
解: (1)当 h = 15 时，
20 t －5 t2 = 15，
t2 － 4 t ＋3 = 0，
t1 = 1， t2 = 3.
当球飞行 1s 和 3s 时，它的高度为 15m .
(t－1) (t－3) = 0
(2)当 h = 20 时，
20 t － 5 t2 = 20，
t2 － 4 t ＋4 = 0，
t1 = t2 = 2.
当球飞行 2s 时，它的高度为 20m .
(3)当 h = 20.5 时，
20 t －5 t2 = 20.5，
t2 － 4 t ＋4.1 = 0，
∵(－4)2－4×1×4.1 ＜ 0 ，
球的飞行高度达不到 20.5 m.
(4)当 h = 0 时，
20 t － 5 t2 = 0，
t2 － 4 t = 0，
t1 = 0， t2 = 4.
当球飞行 0s 和 4s 时，它的高度为 0m ，即 0s时，球从地面飞出，4s 时球落回地面.
t (t－4) = 0，
下列二次函数的图象与 x 轴有交点吗? 若有，求出交点坐标. (1) y=x2＋x－2 (2) y=x2 －6x＋9 (3) y=x2 －x＋1
设 y= 0，解一元二次方程的根.
(1) y = x2＋x－2
解：当 y = 0 时，
∴(x＋2) (x－1) = 0
∴ x1 = －2 ，
∴它与 x 轴有两个交点.
二次函数y = x2＋x－2的图象和x轴交点的横坐标与一元二次方程x2＋x－2=0的根有什么关系?
(2) y = x2－6x＋9
x2－6x＋9 = 0
∴(x－3)2 = 0
∴ x1 = x2=3 ，
∴它与 x 轴只有1个交点.
y = x2－6x＋9
二次函数y = x2－6x＋9的图象和x轴交点的横坐标与一元二次方程x2－6x＋9=0的根有什么关系?
二次函数y=ax2＋bx＋c(a≠0)的图象和x轴交点的横坐标就是对应的一元二次方程ax2＋bx＋c=0(a≠0)的根.
求ax2＋bx＋c=0 (a≠0)的解
x为何值时， y=ax2＋bx＋c的值为0.
确定抛物线y=ax2＋bx＋c与x轴的横坐标.
求ax2＋bx＋c =0(a≠0)的解
(3) y = x2－x＋1
∴它与 x 轴没有交点.
∵(－1)2－4×1×1 ＜ 0 ，
b2 – 4ac > 0
b2 – 4ac = 0
b2 – 4ac < 0
二次函数 y=ax2＋bx＋c 的图象和x轴交点的三种情况与一元二次方程根的关系
ax2＋bx＋c = 0 的根
y=ax2＋bx＋c 的图象与x轴
△ = b2 – 4ac
1.不与x轴相交的抛物线是( ) A. y=2x2－3 B. y=－2x2＋3 C. y=－x2－3x D. y= －2x2－4x－3
2.若抛物线 y=ax2＋bx＋c，当 a>0，c<0时， 图象与x轴交点情况是( ) A. 无交点 B. 只有一个交点 C. 有两个交点 D. 不能确定
3.若抛物线 y=x2＋2x＋m与x轴有两个交点， 则m的取值范围是( ) A. m＞1 B. m＜1 C. 0＜m ≤1 D. m＜－1
4.二次函数 y=mx2 －6x＋3的图象与x轴有交点， 则m的取值范围是( ) A. m＜3 B. m＜3且m≠0 C. m≤3 D. m≤3且m≠0
5.二次函数y=ax2＋bx＋c的图象如图所示， 则下列结论不正确的是( ). A.a＜0 B.c＞0 C.a＋b＋c＞0 D.b2－4ac＞0
6.二次函数y=ax2＋bx＋c的图象如图所示， 那么关于x的方程ax2＋bx＋c－3=0的根的 情况是( ). A.有两个相等的实数根 B.有两个不相等的实数根 C.无实数根 D. 无法确定
7.抛物线y=2x2－4x＋m如图所示，则关于 x的一元二次方程2x2－4x＋m=0的根 是 .
8.抛物线y=x2－2x－3在x轴上截得的线段 长是 .
9.若抛物线y=x2＋bx的对称轴经过(2，0) 则关于x的一元二次方程x2＋bx=5的两个 根是 .
　(1)本节课学了哪些主要内容？ 　(2)二次函数与一元二次方程有什么区别与联系？
二次函数 y=ax2+bx+c 的图象和x轴交点的三种情况与一元二次方程根的关系：