人教版九年级上册22.3 实际问题与二次函数优质课件ppt

这是一份人教版九年级上册22.3 实际问题与二次函数优质课件ppt，共26页。PPT课件主要包含了最大值为，最小值为，－4－，如AB，抛物线，建立适当的坐标系，2－2，拱顶离水面2m，水面宽4m，即OE2等内容，欢迎下载使用。

二次函数是单变量最优化问题的数学模型，如生活中涉及的求最大利润，最大面积等．这体现了数学的实用性，是理论与实践结合的集中体现．本节课主要研究建立坐标系解决实际问题．
学习目标： 能够分析和表示实际问题中变量之间的二次函数关系，正确建立坐标系，并运用二次函数的图象、性质解决实际问题．学习重点： 建立坐标系，利用二次函数的图象、性质解决实际问题．
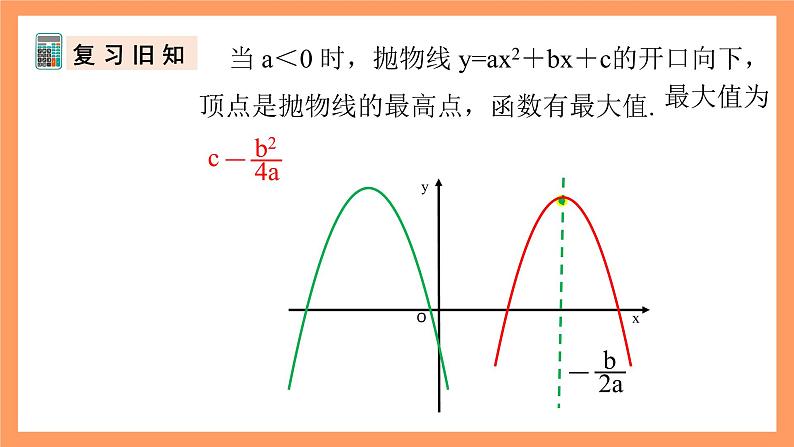
　　当 a＜0 时，抛物线 y=ax2＋bx＋c的开口向下，顶点是抛物线的最高点，函数有最大值.
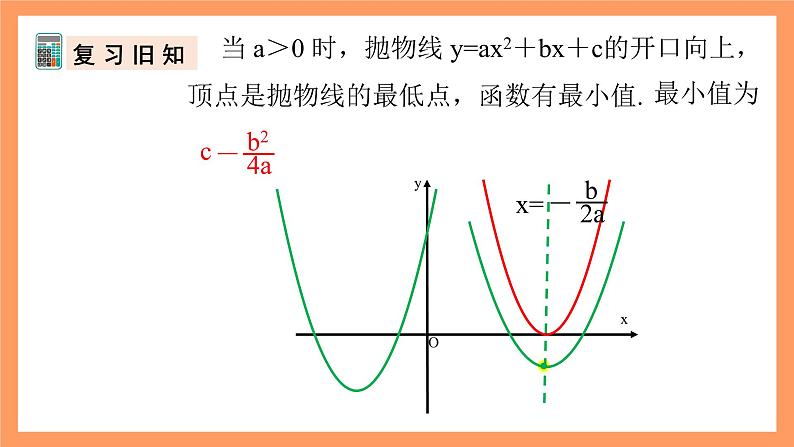
　　 当 a＞0 时，抛物线 y=ax2＋bx＋c的开口向上，顶点是抛物线的最低点，函数有最小值.
∴ 这条抛物线有最低点，
∴它的最低点坐标为(－2，－1).
∴ 这条抛物线开口向上，
∵ b=2 ，c=1，
∵ a= ＞ 0 ，
求下列抛物线最高点或最低点的坐标． 　① y = x2＋2x＋1， ② y =－ x2＋x－4
∴ 这条抛物线有最高点，
∴它的最高点坐标为( 2，3 ).
∵ a=－ ＜0 ，
∴ 这条抛物线开口向下，
∵ b=1 ，c=－4，
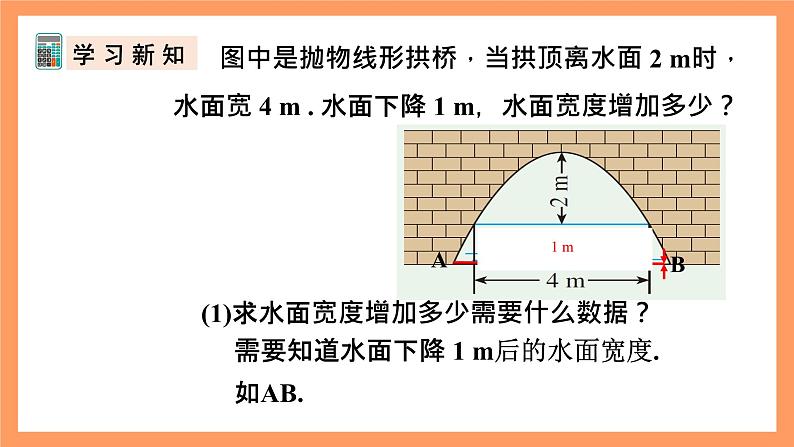
　　图中是抛物线形拱桥，当拱顶离水面 2 m时，水面宽 4 m . 水面下降 1 m，水面宽度增加多少？
(1)求水面宽度增加多少需要什么数据？
需要知道水面下降 1 m后的水面宽度.
(2)表示水面宽度的线段的端点在哪条曲线上？
(2)表示水面宽的线段的端点在哪条曲线上？
(3)如何求出A、B两点的坐标？
要知道A、B两点所在的抛物线解析式.
(3)如何求出A、B 两点的坐标？
(4)怎样确定A、B两点所在的抛物线解析式？
要知道A、B两点所在的抛物线解析式
建立适当的平面直角坐标系.
(5)如何建立直角坐标系？
(4)怎样确定A、B两点 所在的抛物线解析式？
以抛物线的顶点为原点，以抛物线的对称轴为y轴建立平面直角坐标系.
以抛物线的顶点为原点，以抛物线的对称轴 为y轴建立直角坐标系.
设抛物线的解析式为y=ax2.
∵抛物线经过点(2，－2).
∴抛物线的解析式为y=－ x2.
∵当水面下降 1 m时，
∴－3=－ x2
∵抛物线经过点(2，－2)，
∴抛物线的解析式为y=－ x2.
当水面下降 1 m时，
∴－3=－ x2，
∴x1=－ ，
x2= .
水面宽度增加 m.
( －4)
建立适当坐标系解决实际问题的一般步骤:(1)建立适当的直角坐标系；(2)将已知条件转化为点的坐标；(3)合理地设出所求函数的表达式；(4)代人已知条件或点的坐标，求出函数表达式；(5)利用函数表达式求解问题.
根据建立的坐标系选择适当的二次函数表达:(1)顶点在原点，对称轴是y轴，可设函数表达式 为y=ax2；(2)对称轴是y轴,可设函数表达式为y=ax2＋k;(3)顶点在x轴,对称轴平行于y轴，可设函数表达式 为y=a(x＋h)2；(4)抛物线过原点,对称轴平行于y轴,可设函数表达 式为y= ax2＋bx.
3.设计师以函数y=2x2－4x＋8的图象为灵感设计杯子，如图所示.若AB=4，DE=3，则杯子的高 CE=( ). A.17 B.11 C.8 D.7
4.如图是某座抛物线形廊桥的示意图.已知抛物线的函数表达式为y=－ x2＋10.为保护廊桥的安全，在该抛物线上距水面AB高为8m的点 E，F处要安装两盏警示灯，则这两盏灯的水平距离 EF是 m.
5.如图，某工厂车间门口由抛物线和矩形 ABCD的三边组成，门的最大高度是4.9m，AB=10m，BC=2.4m.有一个高4m、宽2m的长方体大型设备要运进车间.如果不考虑其他因素，设备的右侧离门边 m，此设备运进车间时才不致于碰门的顶部.
6.如图的一座拱桥，当水面宽AB为12m时，桥洞顶部离水面4m.已知桥洞的拱形是抛物线，以水平方向为x轴，建立平面直角坐标系.若选取点A为坐标原点，则抛物线的函数表达式是y=－ (x－6)²＋4 ；若选取点B为坐标原点，则抛物线的函数表达是 .
　　(1)这节课学习了用什么知识解决哪类问题？　　(2)解决问题的一般步骤是什么？应注意哪些问题？　　(3)你学到了哪些思考问题的方法？用函数的思想 方法解决抛物线形拱桥问题应注意什么？
课本P52页第3、5题