



人教版九年级上册24.1.1 圆精品课件ppt
展开本课是在学生已经学习了圆的有关概念的基础上开始研究圆的性质,包括圆的轴对称性以及垂径定理,并应用垂径定理及其推论解决问题.
学习目标: 1.理解圆的轴对称性,会运用垂径定理解决有关的 证明、计算和作图问题; 2.感受类比、转化、数形结合、方程等数学思想和 方法,在实验、观察、猜想、抽象、概括、推理 的过程中发展逻辑思维能力和识图能力.学习重点: 垂径定理及其推论.
由此你能得到圆的什么特性?
可以发现:圆是轴对称图形.任何一条直径所在直线都是它的对称轴.
不借助任何工具,你能找到圆形纸片的圆心吗?
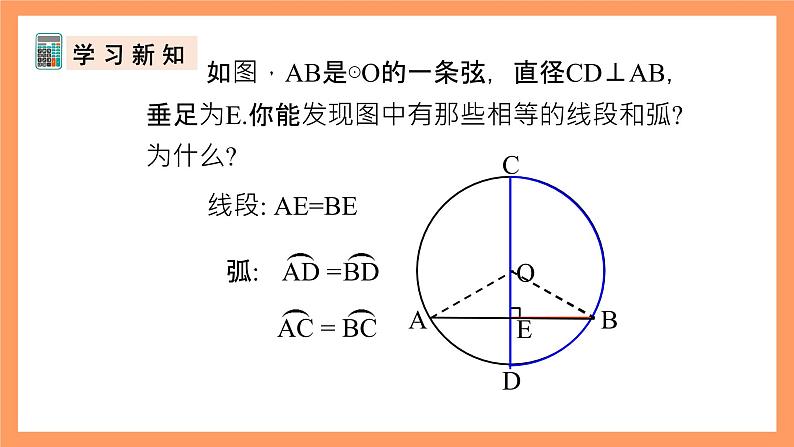
如图,AB是⊙O的一条弦,直径CD⊥AB,垂足为E.你能发现图中有那些相等的线段和弧? 为什么?
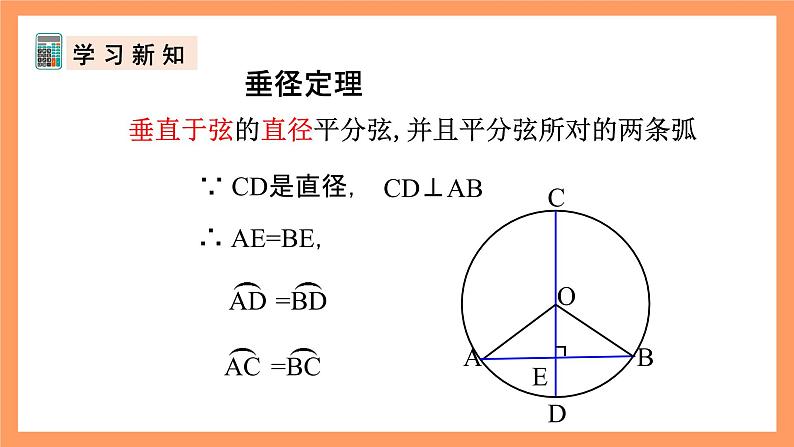
垂直于弦的直径平分弦,并且平分弦所对的两条弧
∵ CD是直径,
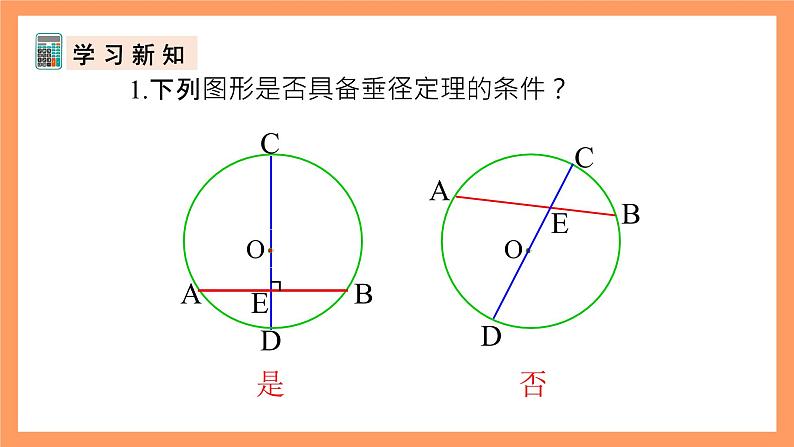
1.下列图形是否具备垂径定理的条件?
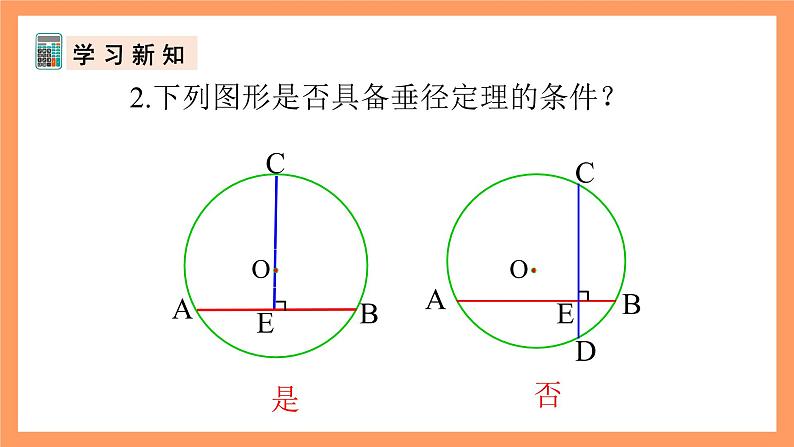
2.下列图形是否具备垂径定理的条件?
3.垂径定理的几个基本图形:
4.如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,则下列结论中不成立的是( )
A.∠COE=∠DOE
例2.如图,在⊙O中,弦AB的长为8cm,圆心O 到 AB的距离为3cm,求⊙O的半径.
解:过点O作OE⊥AB于E,
即⊙O的半径为5cm.
∴AE= AB
在Rt△OAE中,根据勾股定理,
OA2 =AE2+OE2 =42+32=25.
例3 如图,1 400 多年前,我国隋代建造的赵州石拱桥主桥拱是圆弧形,它的跨度(弧所对的弦长)是 37 m,拱高(弧的中点到弦的距离)为 7.23 m,求赵州桥主桥拱的半径(精确到 0.1 m).
解:如图,用弧AB表示主桥拱,设弧AB所在的圆的圆心为O,半径为R.
解:如图,用弧AB表示主桥拱,设弧AB所在的圆的圆心为O,半径为R.
经过圆心O作弦AB的垂线OC,垂足为D,与弧AB交于点C,则D是AB的中点,C是弧AB的中点,CD就是拱高.
∴ AB=37m,CD=7.23m.
∴ AD= AB=18.5m,
∵OA2 =AD2+OD2
解得R=27.3(m).
即主桥拱半径约为27.3m.
OD=OC-CD=R-7.23
∴R2 =18.52+(R-7.23)2
关于弦的问题,常常需要过圆心作弦的垂线段,这是一条非常重要的辅助线。圆心到弦的距离、半径、半弦构成直角三角形,便将问题转化为直角三角形的问题。
1.如图,已知在两同心圆⊙O 中,大圆弦 AB交小圆于C,D,则AC与BD间可能存在什么关系?
答:AC 与 BD 相等.
过点O作OE⊥AB于E,
∴AE-CE=BE-DE ,
变式1 如图,连接 OA,OB,设 AO=BO,求证:AC=BD.
变式2 连接 OC,OD,设 OC=OD,求证:AC=BD.
2.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E.求证:四边形ADOE是正方形.
∴四边形ADOE为矩形,
∴ 四边形ADOE为正方形.
∵OD⊥AB,OE⊥AC,AB⊥AC,
∵OD= AB,
OE= AC,
1.如图,已知OC是⊙O的半径,AB是弦,OC =5,AB=6 ,AB⊥CO于点D,则CD的长 为( ). A. 4 B. 3 C. 2 D. 1
2.如图,AB是⊙O的直径,弦CD⊥AB于点E, 下列结论: ①CE=DE;②BE=OE;③AC=AD; ④∠CAB=∠DAB; ⑤ .一定正确 的个数有( ). A.4个 B.3个 C.2个 D.1个
3.已知⊙O的半径为13cm,弦AB//CD,AB=24cm, CD=10cm,则AB、CD之间的距离为( ). A.12cm B.7cm C.17cm D. 7cm或17cm
① 当 AB与CD在 圆心的同侧时;
②当 AB与CD在 圆心的异侧时;
EF=12 +5=17
4.如图,⊙O的半径OA= cm,弦AB=4cm, 则圆心O到弦AB的距离为 cm.
5.如图,⊙O的直径CD⊥弦AB是于点E,且 CE=1,OB=5 ,则弦AB的长为 .
6.如图,一圆拱桥的拱顶到水面的距离CD为8m, 水面宽AB为8m,则拱桥的OC长为 .
OD2+AD2=OA2
(8-OC)2+42=OC2
64-16OC+OC2+16=OC2
内容: 垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧. ①构造直角三角形,垂径定理和勾股定理有机结合是计算弦长、半径和弦心距等问题的方法. ②技巧:重要辅助线是过圆心作弦的垂线. 重要思路:(由)垂径定理—构造直角三角形— (结合)勾股定理—建立方程.
初中数学人教版九年级上册第二十四章 圆24.1 圆的有关性质24.1.2 垂直于弦的直径评优课ppt课件: 这是一份初中数学人教版九年级上册第二十四章 圆24.1 圆的有关性质24.1.2 垂直于弦的直径评优课ppt课件,共41页。
初中数学人教版九年级上册24.1.2 垂直于弦的直径图片课件ppt: 这是一份初中数学人教版九年级上册24.1.2 垂直于弦的直径图片课件ppt,
初中数学人教版九年级上册24.1.2 垂直于弦的直径备课课件ppt: 这是一份初中数学人教版九年级上册24.1.2 垂直于弦的直径备课课件ppt,共25页。PPT课件主要包含了活动一,实践探究,活动二,活动三,方法总结,课堂小结等内容,欢迎下载使用。













