


初中数学24.1.4 圆周角完整版ppt课件
展开本课是在学习了垂径定理、圆心角及弧、弦、圆心角的关系的基础上探究同弧(或等弧)所对圆周角之间以及圆周角与圆心角之间的数量关系.
学习目标: 1.了解并证明圆周角定理及其推论; 2.经历探究同弧(或等弧)所对圆周角与圆心角之 间的关系的过程,进一步体会分类讨论、转化的 思想方法.学习重点: 圆周角定理.
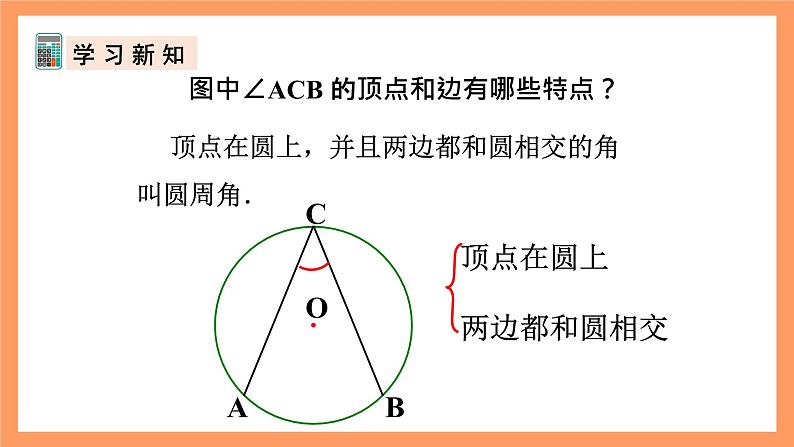
图中∠ACB 的顶点和边有哪些特点?
顶点在圆上,并且两边都和圆相交的角叫圆周角.
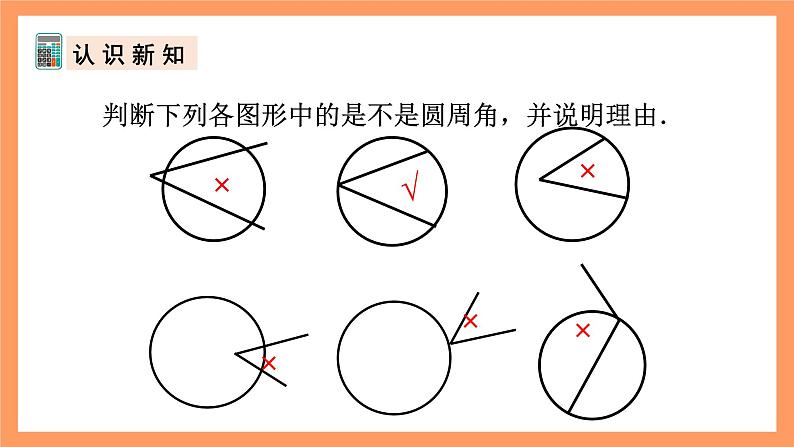
判断下列各图形中的是不是圆周角,并说明理由.
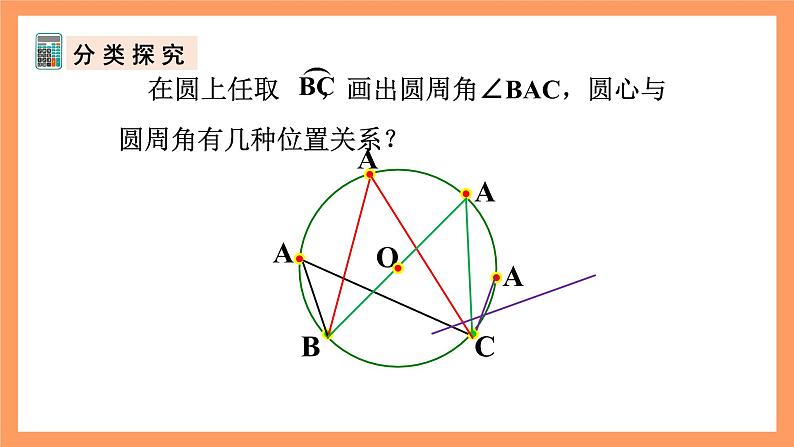
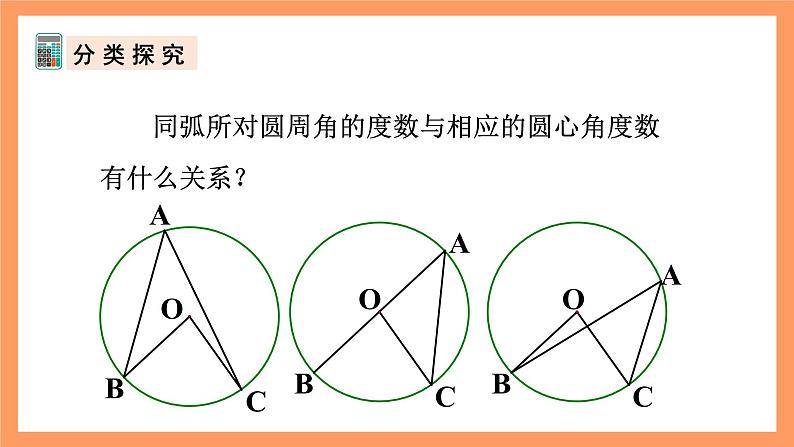
同弧所对圆周角的度数与相应的圆心角度数有什么关系?
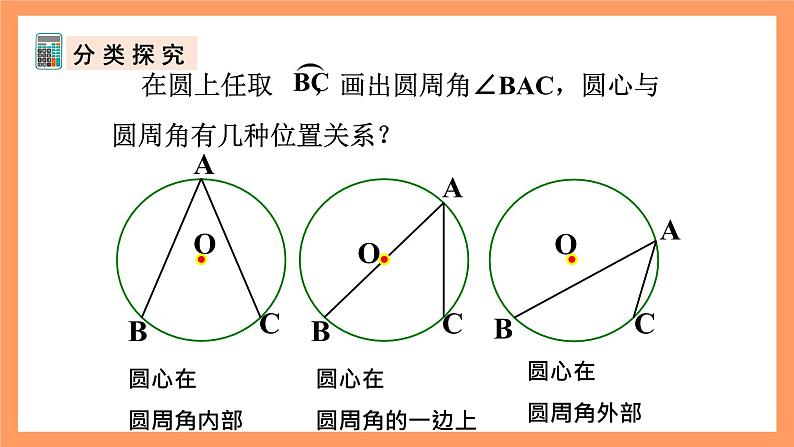
同弧所对圆周角的度数与相应的圆心角度数有什么关系?
(1)当圆心在圆周角的一边上时,
证明:(圆心在圆周角上)
结论:在同圆或等圆中,一条弧所对的圆周角等于它所对圆心角的一半.
∠BAC= ∠BOC.
(2)当圆心在圆周角的内部时,
∴∠BAC= ∠BOC.
∠BAD= ∠BOD,
∠DAC= ∠DOC.
∴∠BAD+∠DAC =
∠BOD+ ∠DOC
= (∠BOD+∠DOC)
(3)当圆心在圆周角的外部时,
∴∠DAC-∠BAD =
∠DOC- ∠BOD
= (∠DOC-∠BOD)
在同圆或等圆中,同弧或等弧所对的圆周角都相等,等于它所对的圆心角的一半.
一条弧所对的圆周角之间有什么关系?同弧或等弧所对的圆周角之间有什么关系?
同弧或等弧所对的圆周角相等.
试找出下图中所有相等的圆周角.
半圆(或直径)所对的圆周角有什么特殊性?
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径.
如图,你能用三角尺确定一张圆形纸片的圆心吗?
例4 如图,⊙O 的直径 AB 为 10 cm,弦 AC 为 6 cm,ACB 的平分线交⊙O 于点 D,求 BC,AD,BD 的长.
∵AB 是⊙O 的直径,
∴ACB=ADB=90°.
在 Rt△ABC 中,
∵ CD 平分ACB,∴ ACD=BCD, ∴ AOD=BOD .∴ AD=BD.在 Rt△ABD 中,AD2+BD2=AB2 ,
∴ AD=BD=
= (cm).
∴AD2= AB2
2. 如图OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC.求证:∠ABC=∠BAC.
∵∠AOB=2∠BOC,
∠AOC+∠BOC =
∴∠AOC =∠BOC,
∴ ,
∴∠ABC=∠BAC.
1.下列四个图中, α是圆周角的为( )
2.如图,A、B、C、D是⊙O上的点,则图中与 A相等的角为( ). A. B B. C C. DEB D. D
3.如图,BC是⊙O的直径,点A是⊙O上异于 B、C的一点,则 A的度数为( ). A.60° B.70° C.80° D.90°
4.如图所示,AB是⊙O的直径,AD=DE, AE与BD交于点C,则图中与∠BCE相等的 角有( ). A.2个 B.3个 C.4个 D.5 个
5.如图,已知CD是⊙O的直径,过点D的弦 DE平行于半径OA,若∠D的度数是50°, 则∠C的度数是( ). A.50° B.40° C.30° D.25°
6.如图,在⊙中O,圆周角 BAC=68°, 则圆心角BOC= °
7.如图,已知点E是圆O上的点, B、C分别是 劣弧 的三等分点,则∠BOC=46°,则 AED的度数是 .
8.如图,AB是⊙O的直径,点C在⊙O上, ∠BAC=30°,点P 在线段OB上运动. 设∠ACP=x,则x的取值范围是 .
(1)本节课学习了哪些主要内容? (2)我们是怎样探究圆周角定理的? 在证明过程中用到了哪些思想方法?
课本P89\90页第5、14题
初中人教版24.1.4 圆周角说课ppt课件: 这是一份初中人教版24.1.4 圆周角说课ppt课件,共18页。PPT课件主要包含了学习目标,圆周角定理的推导,针对训练等内容,欢迎下载使用。
数学九年级上册24.1.4 圆周角背景图课件ppt: 这是一份数学九年级上册24.1.4 圆周角背景图课件ppt,共18页。PPT课件主要包含了合作探究,知识点一,知识点二,∠ACB,∠AOB,∠A∠C,精炼提升,知识点三,COA,同弧或等弧等内容,欢迎下载使用。
人教版七年级上册4.3.1 角教学ppt课件: 这是一份人教版七年级上册4.3.1 角教学ppt课件,共20页。PPT课件主要包含了知识回顾,创设情境引入新知,自主预习,自主探究,角的表示,知识梳理,随堂练习,填一填等内容,欢迎下载使用。













