初中数学人教版九年级上册24.2.2 直线和圆的位置关系试讲课ppt课件

这是一份初中数学人教版九年级上册24.2.2 直线和圆的位置关系试讲课ppt课件，共33页。PPT课件主要包含了点和圆的位置关系，1点在圆内，2点在圆上，3点在圆外，长河落日的景象，直线和圆的位置关系，1直线和圆相离，d＞r，2直线和圆相切，3直线和圆相交等内容，欢迎下载使用。

本课是在研究点和圆的位置关系之后，进一步研究由点组成的直线和圆的位置关系．
学习目标： 1．理解直线和圆相交、相切、相离等概念； 2．理解直线和圆相交、相切、相离的判定方法和性 质．学习重点： 利用圆心到直线的距离与半径的关系判别直线和圆的位置关系．
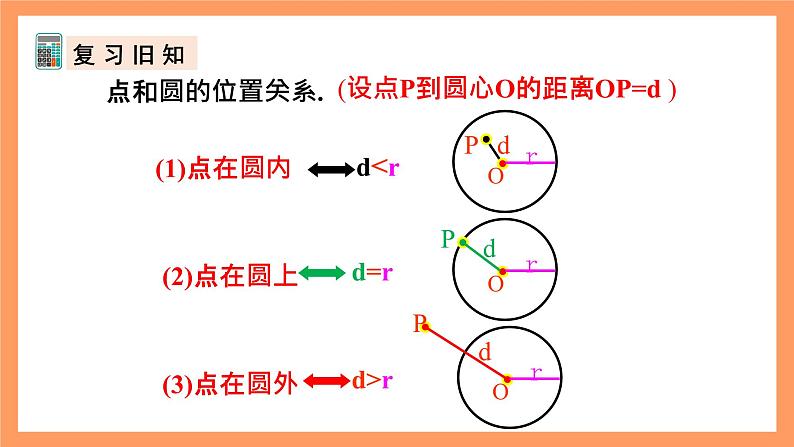
(设点P到圆心O的距离OP=d )
给我们以圆与直线位置关系的形象
　　直线和圆没有公共点时，叫做直线和圆相离．
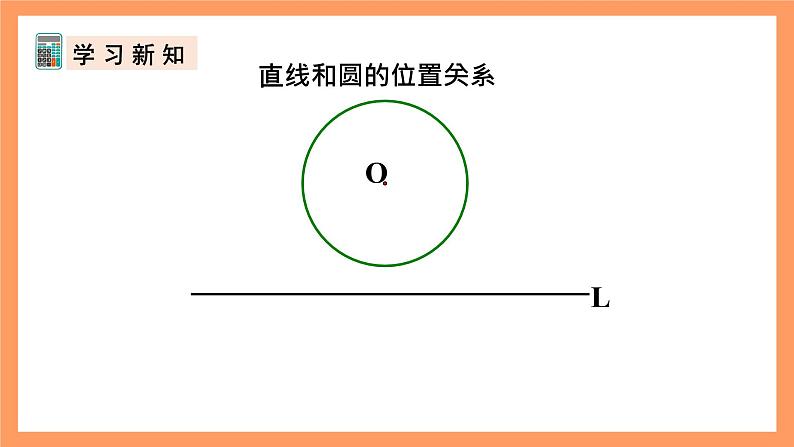
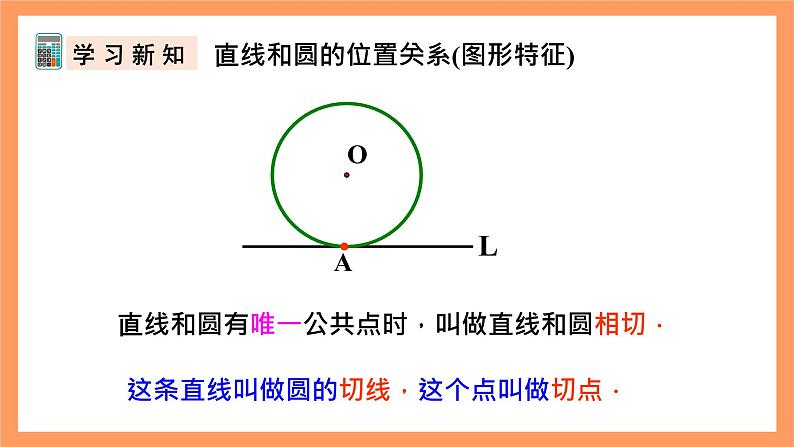
直线和圆的位置关系(图形特征)
直线和圆有唯一公共点时，叫做直线和圆相切．
这条直线叫做圆的切线，这个点叫做切点．
这条直线叫做圆的割线，公共点叫直线和圆的交点．
直线和圆有两个公共点时，叫做直线和圆相交．
　　1.能否根据基本概念判断直线和圆的位置关系？
　　直线 L和⊙O 没有公共点　 直线 L 和⊙O 相离．　　直线 L 和⊙O 只有一个公共点　 直线 L和⊙O 相切．　　直线 L 和⊙O 有两个公共点　 直线 L 和⊙O 相交．
2.是否还有其他的方法判断直线和圆的位置关系？
用公共点的个数来判断直线和圆的位置关系．
直线和圆的位置关系，可从数量关系的角度进行刻画.
(设⊙O的半径为r，圆心O到直线L的距离为d)
(设⊙O的半径为r，圆心O到直线L的距离为d .)
直线和圆的位置关系的三种刻划方法
　　练习1　圆的直径是 13 cm，如果直线和圆心的距离 分别是 ① 4.5 cm；② 6.5 cm；③ 8 cm，那么直线和圆分 别是什么位置关系？有几个公共点？
(1)当 d = 4.5 cm 时，∵ d ＜r，∴直线与圆相交．
(2)当 d = 6.5 cm 时，∵ d = r，∴直线与圆相切．
(3)当 d = 8 cm 时，∵d ＞r，∴直线与圆相离．
∵圆的直径是 13 cm，
∴半径r=6.5cm.
此时直线与圆有2个交点.
此时直线与圆有1个交点.
此时直线与圆相交没有交点.
例题：在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，以C为圆心，r为半径的圆与AB有怎样的位置关系？为什么？ (1)r=2cm； (2)r=2.4cm (3) r=3cm．
例题：在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，判断以点C为圆心，下列r为半径的⊙C与AB的位置： (1)r=2cm； (2)r=2.4cm (3)r=3cm．
分析：　　关键是确定圆心 C 到直线AB 的距离 d.
例题：在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，判断以点C为圆心，下列r为半径的⊙C与AB的位置： (1)r=2cm； (2)r=2.4cm (3) r=3cm．
解：过C作CD⊥AB，垂足为D.
根据三角形的面积公式有
即圆心C到AB的距离d=2.4cm
∴CD · AB=AC · BC
(2)当r=2.4cm时，
(3)当r=3cm时，
因此，⊙C和AB相交.
　　已知圆的直径为13cm，如果圆心到直线的距离为4.5cm，那么直线与圆的位置关系是 ，直线与圆的公共点的个数为____；如果圆心到直线的距离为6.5cm，那么直线与圆的位置关系是 ，直线与圆的公共点的个数为____；如果圆心到直线的距离为8cm，那么直线与圆的位置关系是 ，直线与圆的公共点的个数为____.
1.如图，在矩形ABCD中，AB=3，BC=4，AC为对角线，以点B为圆心，r为半径作⊙B. (1)当半径r= 时，⊙B与AD相切； (2)当半径r= 时，⊙B与CD相切； (3)当半径r= 时，⊙B与AC相切； ．
2.已知⊙O的半径是3，若直线L与⊙O没有公共点，设圆心O到直线L的距离是d ，则d的取值范围是 .
3.如图，已知∠AOB=30°，M为OB上的点，以点M为圆心，2cm 为半径作⊙M，当OM=4cm时，则直线OA与⊙M的位置关系是 .
　 4.已知⊙A 的直径为 6，点 A 的坐标为(－3，－4)，则⊙A 与 x 轴的位置关系是_____，⊙A 与 y 轴的位置关系是______．
　　5.已知⊙O 到直线 L 的距离为 d，⊙O 的半径为 r，若 d、r 是方程 x2 －7x＋12 = 0 的两个根，则直线 L和⊙O 的位置关系是______________．
(x－3) (x－4)=0
6.已知⊙O的直径是12cm，圆心O到直线L的距离 是5cm ，则直线L与⊙ O的公共点个数是 ( ). A.2 B.1 C.0 D.不确定
7.已知⊙O的半径是5cm，点A在直线L上，若OA =5cm ，则直线L与⊙O的位置关系是( ). A.相切 B.相交 C.相切或相交 D.相离
8.已知直线L与半径为R的⊙O相交，且圆心O到 的距离是6 ，则R的取值范围是 ( ). A.R＜6 B.R=6 C.R＞6 D.R≥6
9.已知⊙O到直线 L 的距离为 d，⊙O的半径为 r， 若 d、r 是方程 x2 －4x＋a = 0 的两个根.当直线 L与⊙O相切时，a的值是( ). A.3 B.4 C.5 D.不确定
10.在△ABC中，AB=10cm，AC=6cm，BC=8cm， D、E分别是AC、BC的中点，则以DE为直径 的圆与AB的位置是( ). A.相交 B.相切 C.相离 D.无法确定
　1.直线和圆的位置关系有三种：相离、相切和相交．
　　 2.识别直线和圆的位置关系的方法：　　（1）一种是根据定义进行识别：直线 l 和⊙O 没有公共点　 直线 l 和⊙O 相离；直线 l 和⊙O 只有一个公共点　 直线 l 和⊙O 相切；直线 l 和⊙O 有两个公共点　 直线 l 和⊙O 相交．　　（2）另一种是根据圆心到直线的距离 d 与圆半径 r 的大小关系来进行识别：　　　d ＞r　　直线 l 和⊙O 相离；　　　d ＝r　　直线 l 和⊙O 相切；　　　d ＜r　　直线 l 和⊙O 相交．
3．谈谈这节课你学习的收获．
课本P101页第4、5题