2022-2023学年四川省遂宁市高二（下）期末数学试卷（文科）（含解析）

这是一份2022-2023学年四川省遂宁市高二（下）期末数学试卷（文科）（含解析），共18页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年四川省遂宁市高二（下）期末数学试卷（文科）
一、单选题（本大题共12小题，共60.0分。在每小题列出的选项中，选出符合题目的一项）
1. 已知i是虚数单位，则复数i(1+i)的共轭复数为(    )
A. 1+i B. 1−i C. −1+i D. −1−i
2. 命题“∀x0”的否定为(    )
A. ∀xb”的(    )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
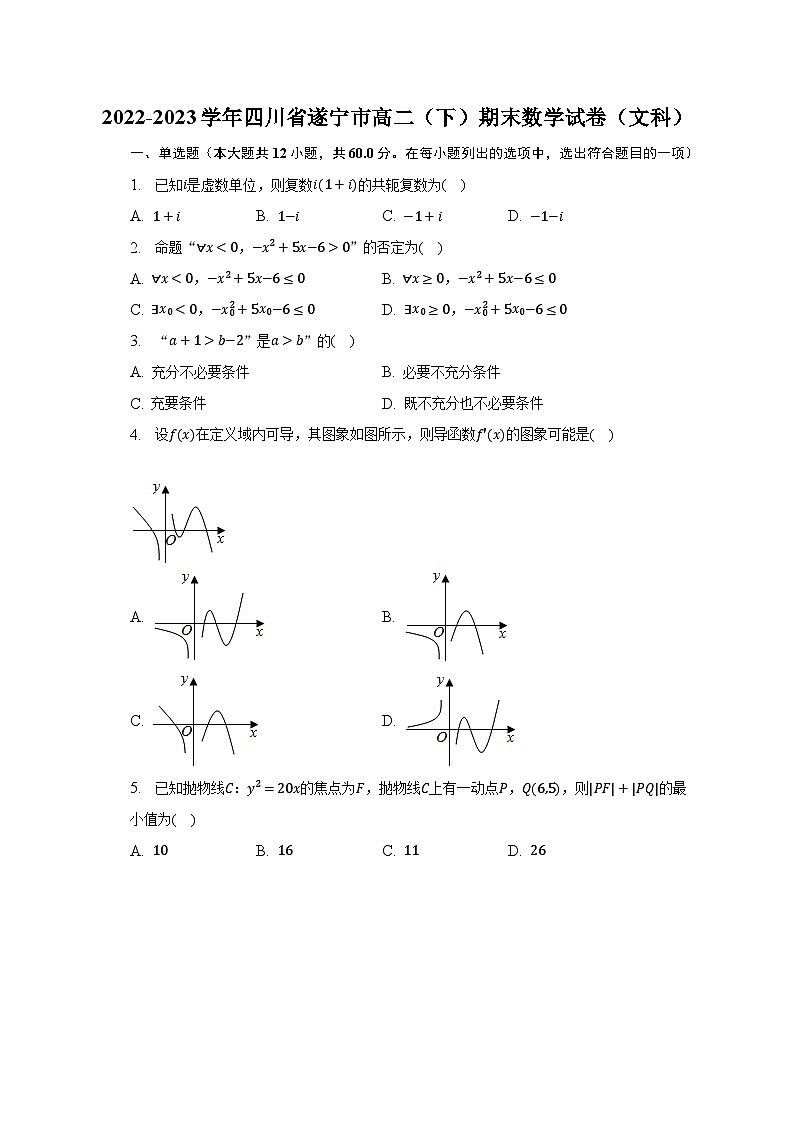
4. 设f(x)在定义域内可导，其图象如图所示，则导函数f′(x)的图象可能是(    )


A. B.
C. D.
5. 已知抛物线C：y2=20x的焦点为F，抛物线C上有一动点P，Q(6,5)，则|PF|+|PQ|的最小值为(    )
A. 10 B. 16 C. 11 D. 26
6. 执行如图所示的算法框图，则输出的l的值为(    )


A. 4 B. 5 C. 6 D. 7
7. “燃脂单车”运动是一种在音乐的烘托下，运动者根据训练者的指引有节奏的踩踏单车，进而达到燃脂目的的运动，由于其操作简单，燃脂性强，受到广大健身爱好者的喜爱.已知某一单车爱好者的骑行速度v(单位：km/h)随时间t(单位：h)变换的函数关系为v(t)=2tet+15，t∈[12,2]，则该单车爱好者骑行速度的最大值为(    )
A. 4e2+15 B. 2e2+15 C. 2e+15 D. 1e12+15
8. 短道速滑队6名队员(含赛前系列赛积分最靠前的甲、乙、丙三名队员在内)进行冬奥会选拔，记“甲得第一名”为p，“乙得第二名”为q，“丙得第三名”为r，若p∨q是真命题，p∧q是假命题，(￢q)∧r是真命题，则选拔赛的结果为(    )
A. 甲得第一名，乙得第二名，丙得第三名
B. 甲得第一名，乙没得第二名，丙得第三名
C. 甲得第一名，乙得第三名，丙得第二名
D. 甲得第二名，乙得第一名，丙得第三名
9. 已知圆C：x2+y2−6x+8=0，若双曲线y2−x2m2=1(m>0)的一条渐近线与圆C相切，则m=(    )
A. 18 B. 24 C. 2 2 D. 8
10. 若函数f(x)=(x−m)2−2,x0
11. 已0b−3成立，故“a+1”>b−2”是a>b”的必要条件，
综上“a+1>b−2”是“a>b”的必要不充分条件，
故选：B．
利用充要条件的定义即可判断．
本题主要考查了充要条件的判断，属于基础题．

4.【答案】B 
【解析】解：由f(x)的图象可得，在y轴的左侧，图象下降，f(x)递减，
即有导数小于0，可排除C，D；
再由y轴的右侧，图象先下降再上升，最后下降，
函数f(x)递减，再递增，后递减，
即有导数先小于0，再大于0，最后小于0，
可排除A；
则B正确．
故选：B．
由f(x)的图象可得在y轴的左侧，图象下降，f(x)递减，y轴的右侧，图象先下降再上升，最后下降，即有y轴左侧导数小于0，右侧导数先小于0，再大于0，最后小于0，对照选项即可判断．
本题考查导数的概念和应用，考查函数的单调性与其导数符号的关系，以及数形结合的思想方法，属于基础题．

5.【答案】C 
【解析】解：设抛物线C的准线为l，作PT⊥l于T，由抛物线的定义知|PF|=|PT|，

所以，当P，Q，T三点共线时，|PF|+|PQ|有最小值，最小值为6+p2=11．
故选：C．
根据抛物线的定义转化为Q到抛物线准线的距离求解即可．
本题考查抛物线的几何性质，数形结合思想，属基础题．

6.【答案】B 
【解析】解：开始i=1，S=12，
①S=12−2=10，i=2，S0)，
将点P的坐标代入抛物线的标准方程得16=4p⇒p=4，
此时，所求抛物线的标准方程为y2=−8x；
当抛物线的焦点在y轴上时，可设所求抛物线的标准方程为x2=−2my(m>0)，
将点P的坐标代入抛物线的标准方程得4=8m，解得m=12，
此时，所求抛物线的标准方程为x2=−y．
综上所述，所求抛物线的标准方程为y2=−8x或x2=−y． 
【解析】(1)根据长轴和焦距的定义求出a、c，进而求出b，即可求解；
(2)设抛物线方程为y2=−2px(p>0)或x2=−2my(m>0)，将点P坐标代入，即可求解．
本题主要考查椭圆、抛物线标准方程的求解，属于基础题．

19.【答案】解：(1)∵y=f(x)过点P(−1,2)，且在点P处的切线恰好与直线x−3y=0垂直，f ′(x)=3ax2+2bx
∴{−a+b=23a−2b=−3,
∴a=1，b=3，
∴f(x)=x3+3x2．
(2)由题意得：f′(x)=3x2+6x=3x(x+2)>0，
解得x>0或x0，求出函数的单调递增区间，据题意知[m,m+1]⊆(−∞，−2]∪[0，+∞)，列出端点的大小，求出m的范围．
注意函数在切点处的导数值是曲线的切线斜率；直线垂直的充要条件是斜率之积为−1．

20.【答案】解：(1)由题意知，x−=1+2+3+4+55=3，y−=120+100+90+75+655=90，
b =i=15xiyi−5x−y−i=15xi2−5x−2=1215−5×3×9055−5×32=−13.5，a =y−−b x−=90+13.5×3=130.5，
所以，回归直线方程为y =−13.5x+130.5；
(2)X2=100×(15×50−25×10)240×25×60×75≈5.556>3.841，
故有95%的把握认为不戴头盔行为与事故伤亡有关． 
【解析】(1)先求得b​,a​，进而求得不戴头盔人数y与月份x之间的回归直线方程；
(2)求得X2的值并与3.841进行大小比较进而得到是否有95%的把握认为不戴头盔行为与事故伤亡有关．
本题主要考查了线性回归方程的求解，还考查了独立性检验的应用，属于中档题．

21.【答案】解：(1)由双曲线的方程可知，双曲线的焦点坐标为(−1,0)，(1,0)，
所以椭圆的焦点坐标为(−1,0)，(1,0)，则c=1，
又椭圆中，由于S△PF1F2=12⋅|F1F2|⋅yP，
所以△PF1F2面积最大值S=12⋅2c⋅b= 3，故b= 3，
则a= b2+c2=2，
所以椭圆C的方程为：x24+y23=1．
(2)证明：设R(x,y)，由于直线过原点，则S(−x,−y)，E(x,0)．
所以直线SE的斜率kSE=y2x=12kRS=12k．
(3)由题设，可设直线l的方程为y=k(x−3)且k≠0，
联立椭圆方程并整理得：(3+4k2)x2−24k2x+36k2−12=0，
则Δ=576k4−48(3+4k2)(3k2−1)>0，
所以Δ=144−240k2>0，
即− 155xM，显然xM0，由f′(x)0时，由f′(x)=0得x=lna，由f′(x)>0得x>lna，由f′(x)0)有两个零点，
令t=xex，则t′=(x+1)ex>0在(0,+∞)上恒成立，
∴t=xex在(0,+∞)上单调递增，
∴h(x)=xex−aln(xex)有两个零点，转化为g(t)=t−alnt有两个零点，
  则g′(t)=1−at=t−at，t∈(0,+∞)，
∴①当a≤0时，g′(t)>0，即g(t)在(0,+∞)上单调递增，不可能有两个零点；
②当a>0时，由g′(t)>0得t>a，由g′(t)0)有两个零点，令t=xex，则t′=(x+1)ex>0在(0,+∞)上恒成立，即t=xex在(0,+∞)上单调递增，h(x)=xex−aln(xex)有两个零点，即g(t)=t−alnt有两个零点，利用导数研究g(t)，即可得出答案．
本题考查利用导数研究函数的单调性、极值和最值，考查转化思想、分类讨论思想，考查逻辑推理能力和运算能力，属于中档题．