初中数学人教版八年级上册13.3.2 等边三角形教学ppt课件

这是一份初中数学人教版八年级上册13.3.2 等边三角形教学ppt课件，文件包含1334含30°角的直角三角形的性质pptx、1334含30°角的直角三角形的性质同步练习解析版docx、1334含30°角的直角三角形的性质教学设计docx、1334含30°角的直角三角形的性质同步练习原卷版docx、1334含30°角的直角三角形的性质导学案docx等5份课件配套教学资源，其中PPT共30页， 欢迎下载使用。

13.3.4 含30°角的直角三角形的性质
人教版数学八年级上册
1．探索含30°角的直角三角形的性质．（重点）2．会运用含30°角的直角三角形的性质进行有关的证明和计算．（难点）
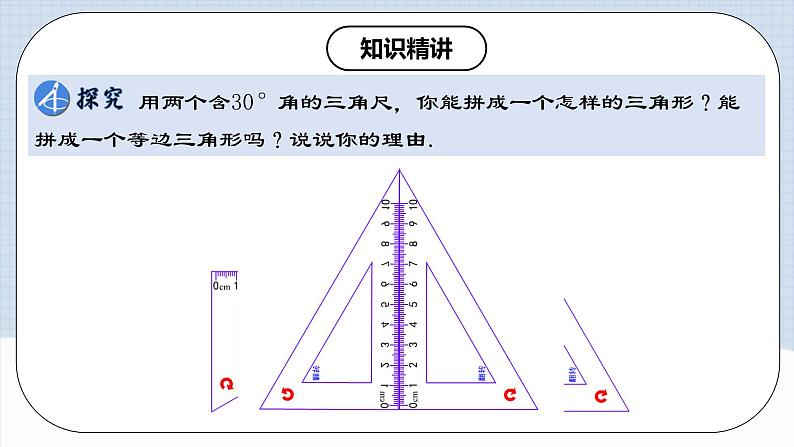
用两个含30°角的三角尺，你能拼成一个怎样的三角形？能拼成一个等边三角形吗？说说你的理由.
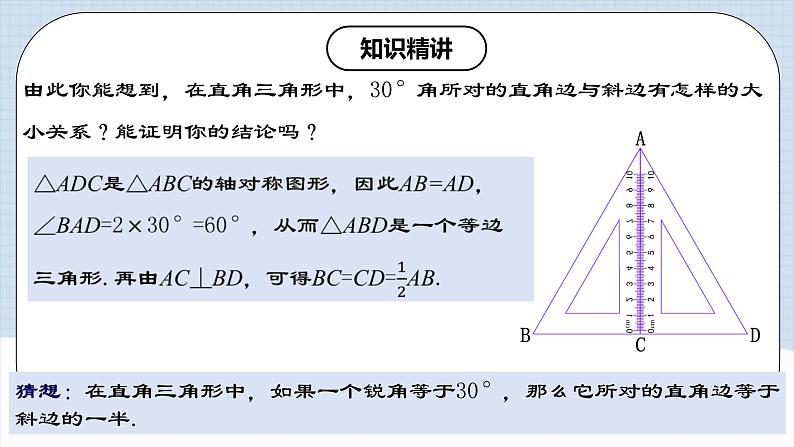
由此你能想到，在直角三角形中，30°角所对的直角边与斜边有怎样的大小关系？能证明你的结论吗？
 
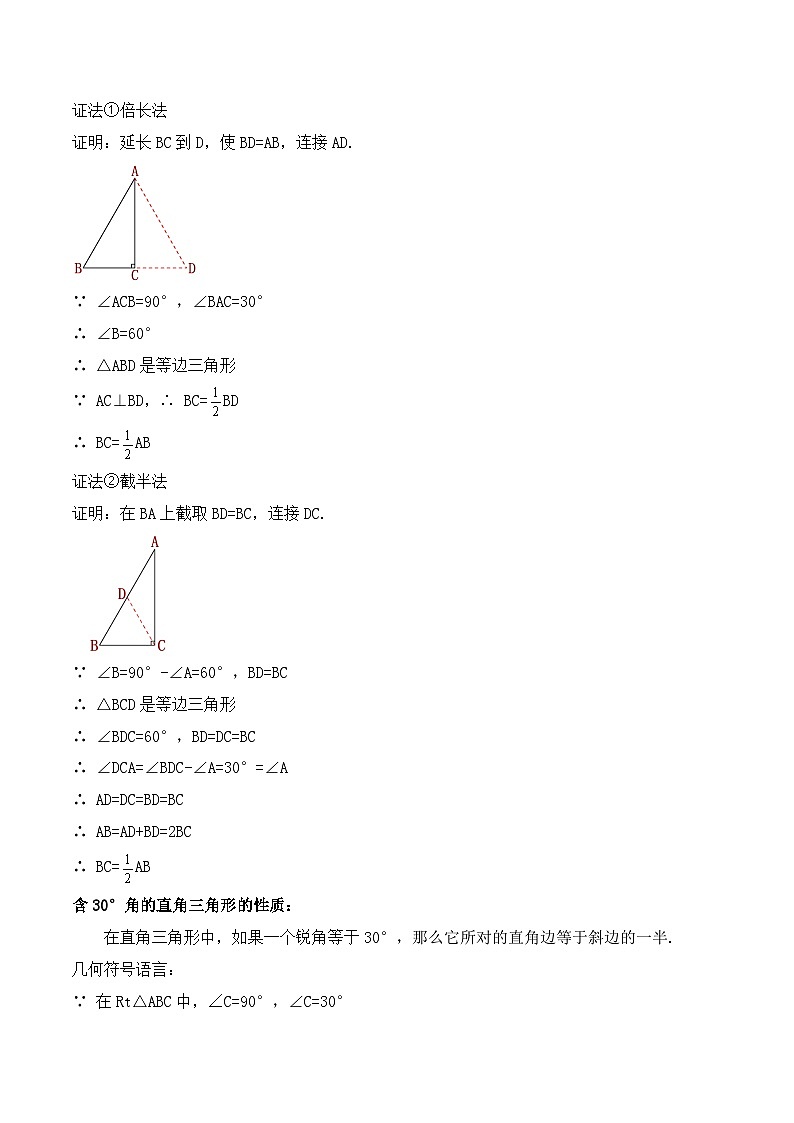
猜想：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.
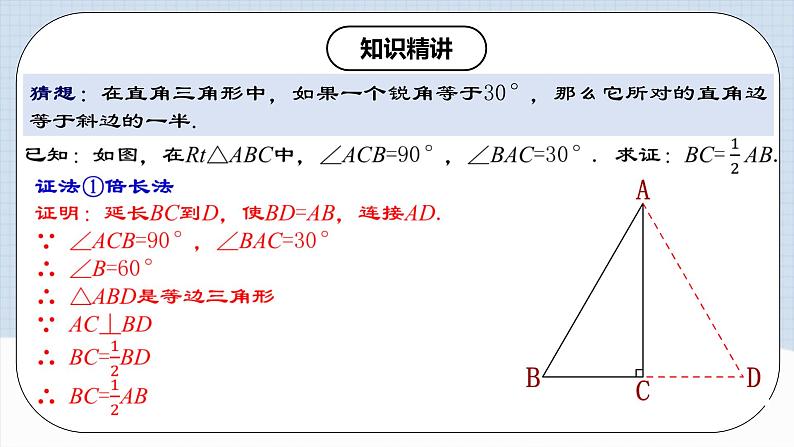
猜想：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.
 
 
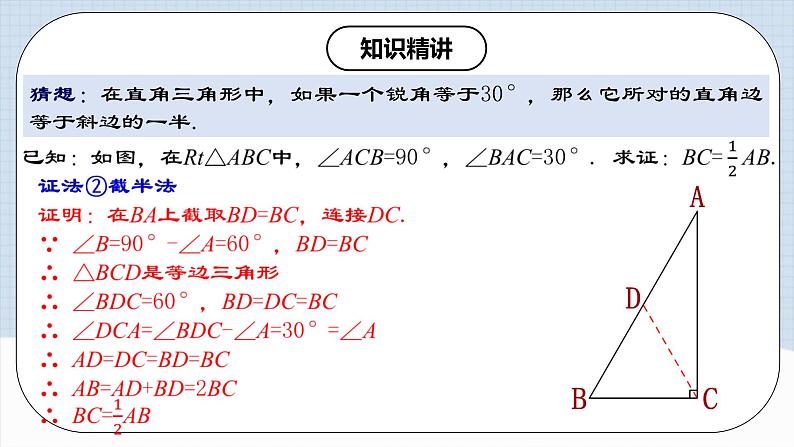
猜想：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.
 
 
含30°角的直角三角形的性质： 在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.
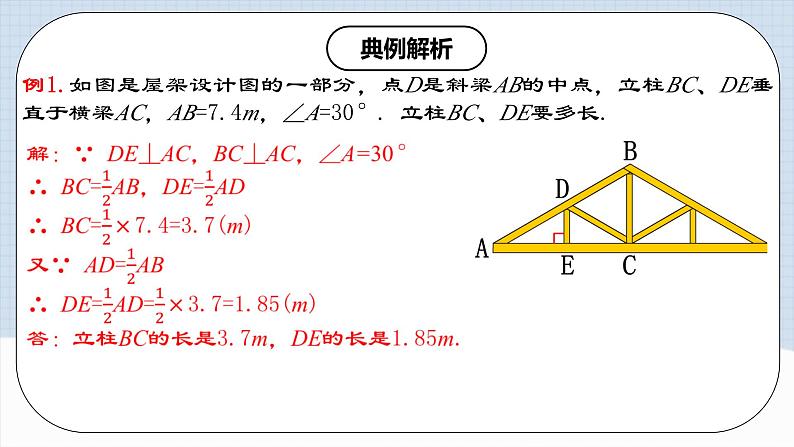
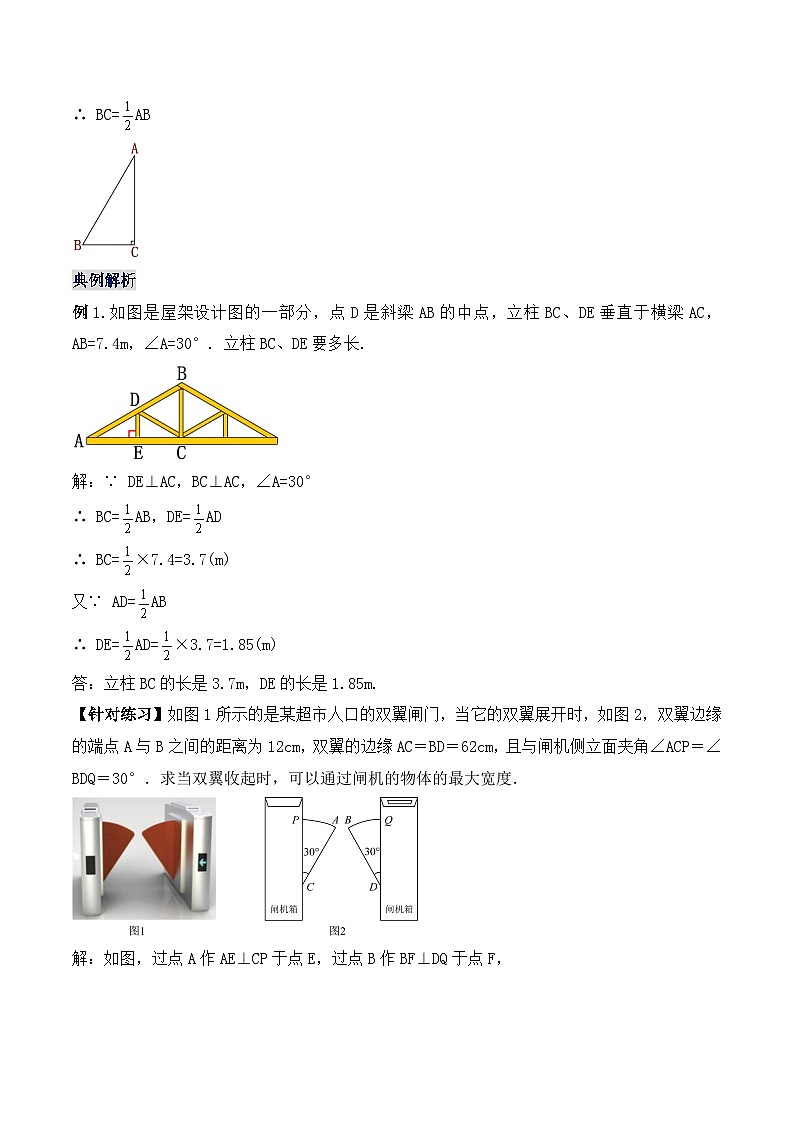
例1.如图是屋架设计图的一部分，点D是斜梁AB的中点，立柱BC、DE垂直于横梁AC，AB=7.4m，∠A=30°. 立柱BC、DE要多长.
 
如图1所示的是某超市人口的双翼闸门，当它的双翼展开时，如图2，双翼边缘的端点A与B之间的距离为12cm，双翼的边缘AC＝BD＝62cm，且与闸机侧立面夹角∠ACP＝∠BDQ＝30°．求当双翼收起时，可以通过闸机的物体的最大宽度．
 
例2.如图，在△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F．求证:BF=2CF.
证明:连接AF.∵EF是AC的垂直平分线∴AF=CF∴∠C=∠FAC∵AB=AC，∠BAC=120°∴∠B=∠C=∠FAC=30°∴∠BAF=120°-30°=90°∴BF=2AF∴BF=2CF
如图，点D在线段BC上，连接AD，BD=CD，CA⊥AD，∠1=30°，AB=4，求AC的长．
 
例3.如图，等边△ABC的边长为8，D为AB边上一动点，过点D作DE⊥BC于点E，过点E作EF⊥AC于点F.(1)若AD=2，求AF的长;(2)当AD取何值时，DE=EF?
 
 
例3.如图，等边△ABC的边长为8，D为AB边上一动点，过点D作DE⊥BC于点E，过点E作EF⊥AC于点F.(1)若AD=2，求AF的长;(2)当AD取何值时，DE=EF?
 
如图，Rt△ACB中，∠ACB=90°，∠A=30°，∠ABC的平分线BE交AC于点E．点D为AB上一点，且AD=AC，CD、BE交于点M.(1)求∠DMB的度数;
(1)解:∵∠ACB=90°，∠A=30°∴∠ABC=60°∴BE是∠ABC的平分线∴∠ABE=∠CBE=30°∵∠A=30°，AC=AD∴∠ACD=∠ADC=75°∴∠DMB=∠ADC-∠ABE=45°
(2)证明:∵∠ACB=90°，∠A=30°∴AB=2BC∵CH⊥BE，∠CBE=30°∴BC=2CH ∴AB=4CH∵∠CMH=∠DMB=45°∴∠CMH=∠MCH=45°∴CH=MH∴AB=4MH
如图，Rt△ACB中，∠ACB=90°，∠A=30°，∠ABC的平分线BE交AC于点E．点D为AB上一点，且AD=AC，CD、BE交于点M. (2)若CH⊥BE于点H，求证:AB=4MH.
例4.已知，如图，△ABC为等边三角形，点E在AC边上，点D在BC边上，并且AE＝CD，AD和BE相交于点M，BN⊥AD于N．(1)求证：BE＝AD；(2)求∠BMN的度数；(3)若MN＝3cm，ME＝1cm，则AD＝　 　cm．
例4.已知，如图，△ABC为等边三角形，点E在AC边上，点D在BC边上，并且AE＝CD，AD和BE相交于点M，BN⊥AD于N．(1)求证：BE＝AD；
 
例4.已知，如图，△ABC为等边三角形，点E在AC边上，点D在BC边上，并且AE＝CD，AD和BE相交于点M，BN⊥AD于N．(2)求∠BMN的度数；
 
例4.已知，如图，△ABC为等边三角形，点E在AC边上，点D在BC边上，并且AE＝CD，AD和BE相交于点M，BN⊥AD于N．(3)若MN＝3cm，ME＝1cm，则AD＝　 　cm．
 
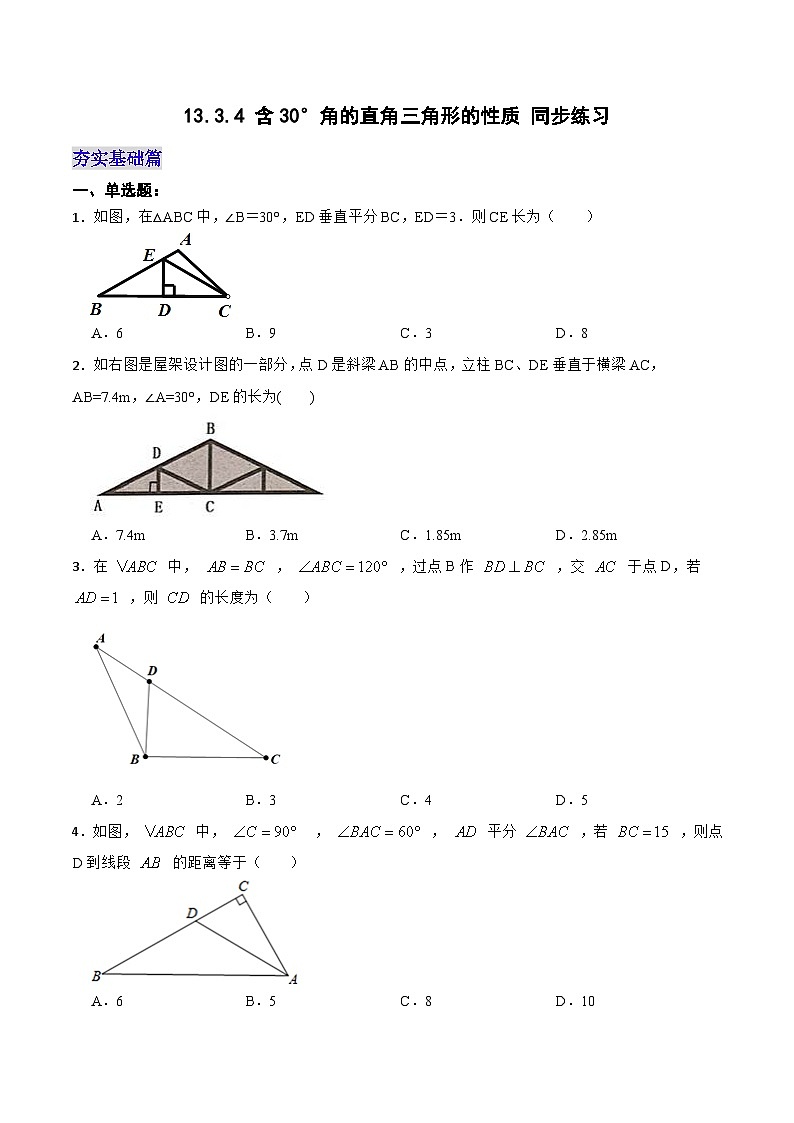
1.如图(1)，△ABC中，∠C=90°，AC=3，∠B=30°，点P是BC边上的动点，则AP长不可能是( )A.3.5 B.4.2 C.5.8 D.7
D
2.如图(2)，是某商场一楼与二楼之间的手扶电梯示意图．其中AB，CD分别表示一楼，二楼地面的水平线，∠ABC=150°，BC的长是8m，则乘电梯从点B到点C上升的高度h是( )A.3m B.4m C.5m D.6m
B
3.如图，在Rt△ABC中，∠C=90°，DE垂直平分AB，垂足为D,交BC于E，AE平分∠BAC，那么下列关系式中不成立的是( )A.∠B=∠CAE B.∠DEA=∠CEA C.AB=2AC D.AC=2EC
D
4.已知一个三角形的三个内角的比是1:2:3，最短边为5cm,则最长边为_____cm.5.如图，AB=AC，∠BAC=120°，D是BC的中点，DE⊥AB于E，若AD=3cm，则AB=____cm，BE=_____cm.
10
6
4.5
6.如图(3)，∠BAC=30°，AM是∠BAC的平分线，过点M作ME∥BA交AC于点E，作MD⊥BA，垂足为D，ME=10cm，则MD=_____cm.7.将一副三角尺按如图(4)所示方式叠放在一起,若AB=16cm，则阴影部分的面积是_____cm2.
5
32
8.Rt△ABC中，∠C=90°，∠B=2∠A，∠B和∠A各是多少度？边AB与BC之间有什么关系？
 
9.如图，在Rt△ABC中，∠C=90°, ∠BAC=60°，∠BAC的平分线AM长为15cm，求BC的长.
 
10.如图，在△ABC中，∠C＝90°，AD是∠BAC的平分线，过点D作DE⊥AB.DE恰好是∠ADB的平分线．CD与DB有怎样的数量关系？请说明理由．
理由如下：∵DE⊥AB，∴∠AED＝∠BED＝90°.
∵DE是∠ADB的平分线，∴∠ADE＝∠BDE.
又∵DE＝DE，∴△AED≌△BED(ASA)，
在Rt△ACD中，∵∠CAD＝30°，
∴AD＝BD，∠DAE＝∠B.
∴∠BAD＝∠CAD＝∠B.
∵∠BAD＋∠CAD＋∠B＝90°，
∴∠B＝∠BAD＝∠CAD＝30°.
含30°角的直角三角形的性质： 在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.