













所属成套资源:2024新人教版数学初二上学期课件PPT+教案+分层作业(学生+教师)+导学案整册
人教版八年级上册13.2.1 作轴对称图形教学ppt课件
展开
这是一份人教版八年级上册13.2.1 作轴对称图形教学ppt课件,文件包含1321画轴对称图形pptx、1321画轴对称图形同步练习解析版docx、1321画轴对称图形教学设计docx、1321画轴对称图形同步练习原卷版docx、1321画轴对称图形导学案docx、例1mp4、利用轴对称设计图案mp4、归纳演示mp4、情境引入mp4、练习1mp4、练习2mp4、问题1mp4、问题2mp4等13份课件配套教学资源,其中PPT共22页, 欢迎下载使用。
人教版初中数学八年级上册13.2.1 画轴对称图形 教学设计一、教学目标:1.能够按要求画简单平面图形经过一次对称后的图形. 2.掌握作轴对称图形的方法. 3.通过画轴对称图形,增强学生学习几何的趣味感.二、教学重、难点:重点:会画已知图形关于某直线的轴对称图形.难点:理解轴对称性质在作图中的运用.三、教学过程:情境引入动手操作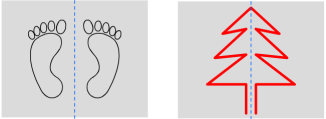 归纳由一个平面图形可以得到它关于一条直线l对称的图形,这个图形与原图形的形状、大小完全一样;新图形上的每一点都是原图形上的某一点关于直线l的对称点;连接任意一对对应点的线段被对称轴垂直平分.知识精讲问题1:已知对称轴m和一点A,要画出点A关于m的对称点A′,如何画呢?
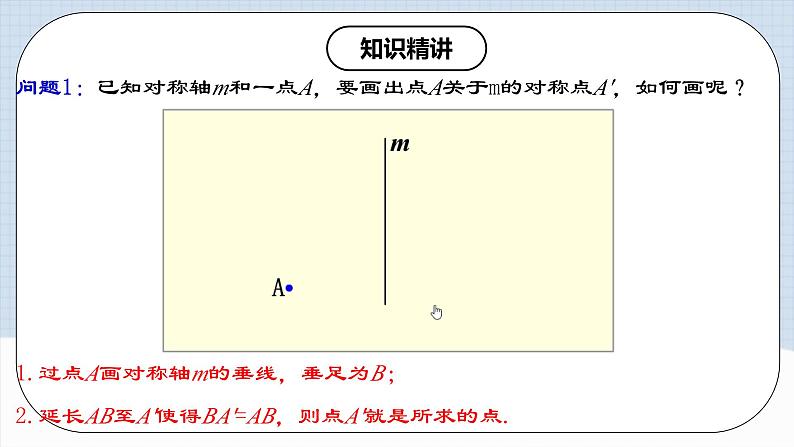
归纳由一个平面图形可以得到它关于一条直线l对称的图形,这个图形与原图形的形状、大小完全一样;新图形上的每一点都是原图形上的某一点关于直线l的对称点;连接任意一对对应点的线段被对称轴垂直平分.知识精讲问题1:已知对称轴m和一点A,要画出点A关于m的对称点A′,如何画呢? 1.过点A画对称轴m的垂线,垂足为B;2.延长AB至A′使得BA′=AB,则点A′就是所求的点.
1.过点A画对称轴m的垂线,垂足为B;2.延长AB至A′使得BA′=AB,则点A′就是所求的点. 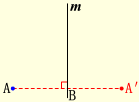 问题2:如何画一条线段的对称图形?
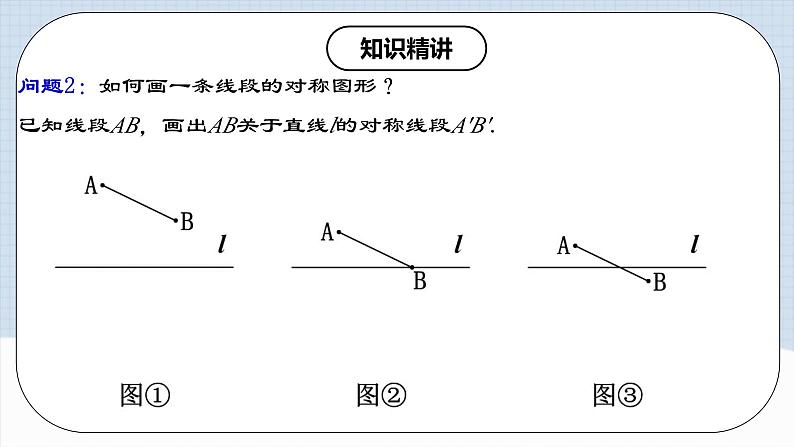
问题2:如何画一条线段的对称图形?
已知线段AB,画出AB关于直线l的对称线段A′B′.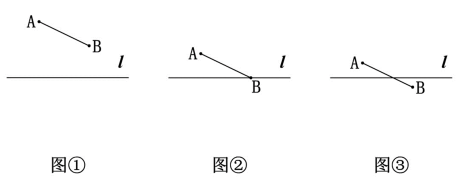
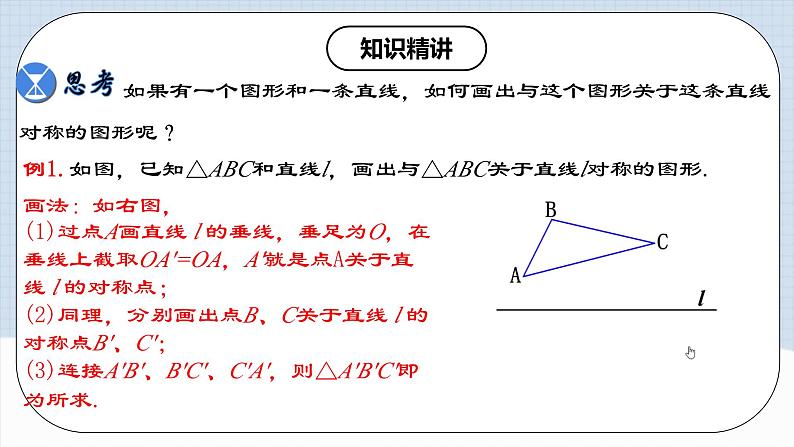
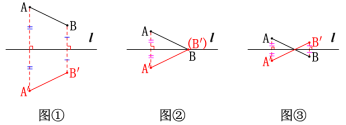 思考:如果有一个图形和一条直线,如何画出与这个图形关于这条直线对称的图形呢?典例解析例1.如图,已知△ABC和直线l,画出与△ABC关于直线l对称的图形.
思考:如果有一个图形和一条直线,如何画出与这个图形关于这条直线对称的图形呢?典例解析例1.如图,已知△ABC和直线l,画出与△ABC关于直线l对称的图形.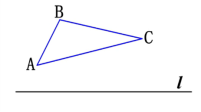 画法:如下图,
画法:如下图,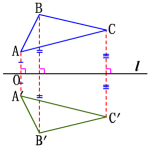 (1)过点A画直线 l 的垂线,垂足为O,在垂线上截取OA′=OA,A′就是点A关于直线 l 的对称点;
(1)过点A画直线 l 的垂线,垂足为O,在垂线上截取OA′=OA,A′就是点A关于直线 l 的对称点;
(2)同理,分别画出点B、C关于直线 l 的对称点B′、C′;
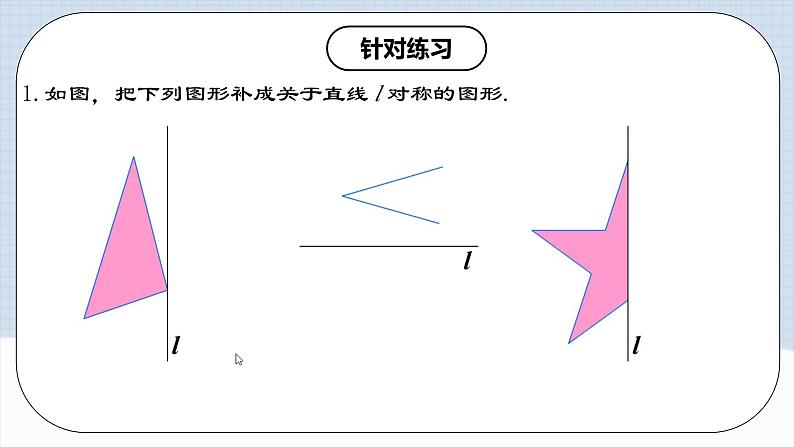
(3)连接A′B′、B′C′、C′A′,则△A′B′C′即为所求.归纳:几何图形都可以看作由点组成,对于某些图形,只要画出图形中的一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.下图是一个图案的一半,其中的虚线是这个图案的对称轴,画出这个图案的另一半.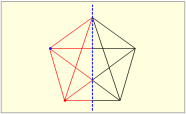 【针对练习】1.如图,把下列图形补成关于直线 l 对称的图形.
【针对练习】1.如图,把下列图形补成关于直线 l 对称的图形.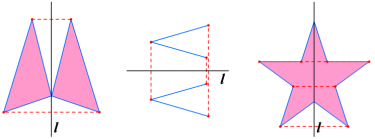 2.用纸片剪一个三角形,分别沿它一边的中线、高、角平分线对折,看看哪些部分能够重合,哪些部分不能重合?
2.用纸片剪一个三角形,分别沿它一边的中线、高、角平分线对折,看看哪些部分能够重合,哪些部分不能重合?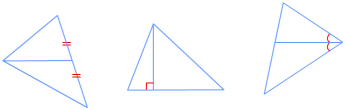 美术作品利用轴对称,可以设计出精美的图案. 在许多美术作品中,都能看到轴对称的例子.
美术作品利用轴对称,可以设计出精美的图案. 在许多美术作品中,都能看到轴对称的例子. 例2.将一张正方形纸片按如图①,图②所示的方向对折,然后沿图③中的虚线剪裁得到图④,将图④的纸片展开铺平,再得到的图案是( )
例2.将一张正方形纸片按如图①,图②所示的方向对折,然后沿图③中的虚线剪裁得到图④,将图④的纸片展开铺平,再得到的图案是( )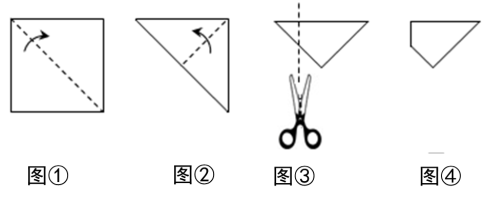
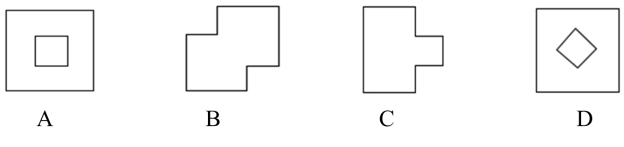 【针对练习】如图,将标号为A、B、C、D的正方形沿图中的虛线剪开后,得到标号为P、Q、M、N的四组图形,试按照“哪个正方形剪开后得到哪组图形”的对应关系,填空: A与____对应;B与____对应; C与____对应;D与____对应.
【针对练习】如图,将标号为A、B、C、D的正方形沿图中的虛线剪开后,得到标号为P、Q、M、N的四组图形,试按照“哪个正方形剪开后得到哪组图形”的对应关系,填空: A与____对应;B与____对应; C与____对应;D与____对应.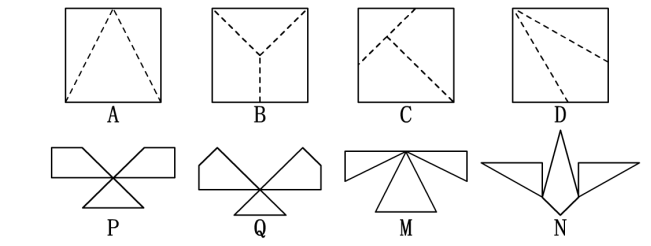 例3.在3×3的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在下面给出的图中画出4个这样的△DEF.
例3.在3×3的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在下面给出的图中画出4个这样的△DEF.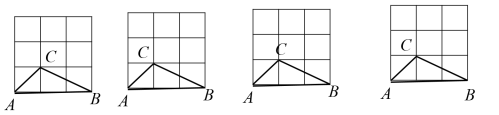
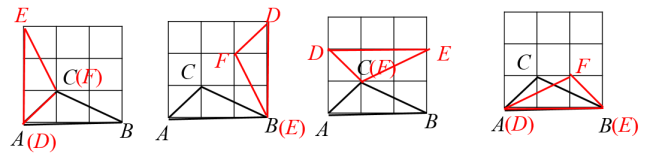 【点睛】作一个图形关于一条已知直线的对称图形,关键是作出图形上一些点关于这条直线的对称点,然后再根据已知图形将这些点连接起来.课堂小结1.本节课你有哪些收获?2.还有没解决的问题吗?【设计意图】培养学生概括的能力。使知识形成体系,并渗透数学思想方法。达标检测1.下列各图分别以直线l为对称轴,所作轴对称图形错误的是( )
【点睛】作一个图形关于一条已知直线的对称图形,关键是作出图形上一些点关于这条直线的对称点,然后再根据已知图形将这些点连接起来.课堂小结1.本节课你有哪些收获?2.还有没解决的问题吗?【设计意图】培养学生概括的能力。使知识形成体系,并渗透数学思想方法。达标检测1.下列各图分别以直线l为对称轴,所作轴对称图形错误的是( )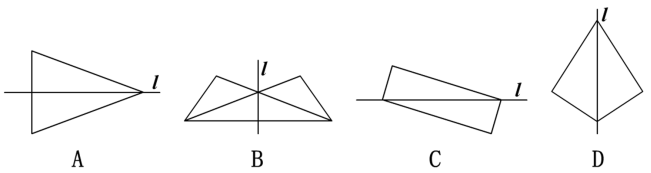 2.如图,在3×3的方格图中,再将其中一个小方格的中心画上半径相等的圆,使整个图形为轴对称图形,方法有( )A.1种 B.2种 C.3种 D.4种
2.如图,在3×3的方格图中,再将其中一个小方格的中心画上半径相等的圆,使整个图形为轴对称图形,方法有( )A.1种 B.2种 C.3种 D.4种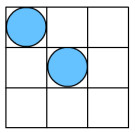 3.如图,将矩形纸片先沿虚线AB按箭头方向向右对折,接着将对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )
3.如图,将矩形纸片先沿虚线AB按箭头方向向右对折,接着将对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )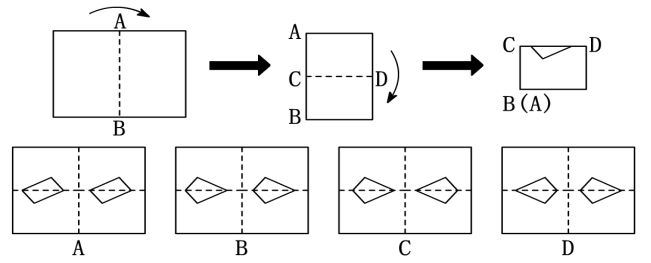 4.如图,画△ABC关于直线l的对称图形.
4.如图,画△ABC关于直线l的对称图形.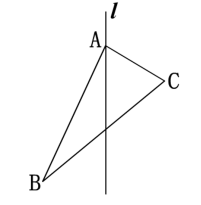 5.如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC.(1)在图中作出△ABC关于直线l对称的△A1B1C1;(2)在(1)问的结果下,连接BB1,CC1, 求四边形BB1C1C的面积.
5.如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC.(1)在图中作出△ABC关于直线l对称的△A1B1C1;(2)在(1)问的结果下,连接BB1,CC1, 求四边形BB1C1C的面积.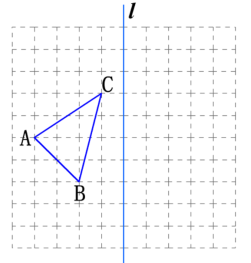 6.如图,C、D、E、F是一个长方形台球桌的4个顶点,A、B是桌面上的两个球,怎样击打A球,才能使A球撞击桌面边缘CF后反弹能够撞击B球?请画出A球经过的路线,并写出作法.
6.如图,C、D、E、F是一个长方形台球桌的4个顶点,A、B是桌面上的两个球,怎样击打A球,才能使A球撞击桌面边缘CF后反弹能够撞击B球?请画出A球经过的路线,并写出作法.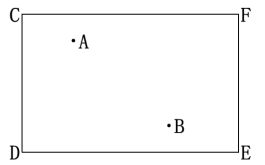 7.如图,等边三角形ABC的边长为3cm,D, E分别是AB,AC上的点,将△ADE沿直线DE折叠,使点A落在A'处,且点A'在△ABC外部,求阴影部分图形的周长.
7.如图,等边三角形ABC的边长为3cm,D, E分别是AB,AC上的点,将△ADE沿直线DE折叠,使点A落在A'处,且点A'在△ABC外部,求阴影部分图形的周长.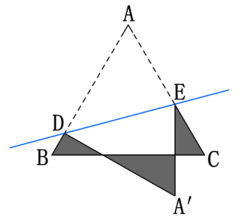 【参考答案】CCD解:如图所示,△A'B'C' 为所求.
【参考答案】CCD解:如图所示,△A'B'C' 为所求.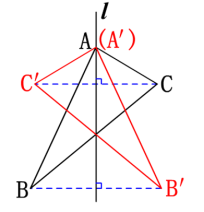 5. 解:(1)如图,△A1B1C1为所求;
5. 解:(1)如图,△A1B1C1为所求;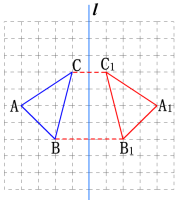 (2)连接BB1,CC1.S四边形BB1C1C=(2+4)×4÷2=126. 解:如图,作点A关于直线CF对称的点A',连接A' B交CF于点P,则点P即为A球撞击桌面边缘CF的位置.连接AP,折线APB即为A球经过的路线.
(2)连接BB1,CC1.S四边形BB1C1C=(2+4)×4÷2=126. 解:如图,作点A关于直线CF对称的点A',连接A' B交CF于点P,则点P即为A球撞击桌面边缘CF的位置.连接AP,折线APB即为A球经过的路线.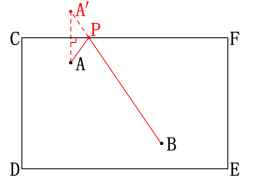 7. 解:依题意,可知△A'DE≌△ADE∴A'D=AD,A'E=AE∴A' D+BD=AD+BD=AB A' E+CE=AE+CE=AC∴ C阴影=A' D+BD+A' E+CE+BC=AB+AC+BC=3+3+3=9(cm)四、教学反思:本节课尽量创设与学生生活环境、知识背景相关的教学情境,以生动活泼的形式呈现有关内容. 重视动手操作,实践探究,但如果只有操作,而没有数学体验,数学课很容易上成劳技课,所以本节课的设计在重视活动的同时,又重视知识的获取,因为动手操作的目的本身就在于更直观地发现新知识. 练习的设计具有一定的层次性,使不同的学生在学习数学的过程中得到不同的发展.
7. 解:依题意,可知△A'DE≌△ADE∴A'D=AD,A'E=AE∴A' D+BD=AD+BD=AB A' E+CE=AE+CE=AC∴ C阴影=A' D+BD+A' E+CE+BC=AB+AC+BC=3+3+3=9(cm)四、教学反思:本节课尽量创设与学生生活环境、知识背景相关的教学情境,以生动活泼的形式呈现有关内容. 重视动手操作,实践探究,但如果只有操作,而没有数学体验,数学课很容易上成劳技课,所以本节课的设计在重视活动的同时,又重视知识的获取,因为动手操作的目的本身就在于更直观地发现新知识. 练习的设计具有一定的层次性,使不同的学生在学习数学的过程中得到不同的发展.
相关课件
这是一份初中数学人教版八年级上册13.2.1 作轴对称图形教案配套课件ppt,共13页。PPT课件主要包含了花边艺术,哈我知道怎样作等内容,欢迎下载使用。
这是一份数学八年级上册13.2.1 作轴对称图形习题课件ppt,共16页。
这是一份数学八年级上册13.2.1 作轴对称图形课文ppt课件,共20页。PPT课件主要包含了征集设计方案,情景创设,想一想,尝试探究,试一试,欣赏和设计,加油哦,拓展练习等内容,欢迎下载使用。










