

2022-2023学年重庆市合川区七年级(下)期末数学试卷(含解析)
展开2022-2023学年重庆市合川区七年级(下)期末数学试卷
第I卷(选择题)
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下面调查中,最适宜采用全面调查的是( )
A. 了解市场上奶茶的质量 B. 了解一次性餐盒的卫生状况
C. 了解某型号智能手表的电池寿命 D. 了解一个班级的视力情况
2. 在平面直角坐标系中,下列各点位于第四象限的是( )
A. (−3,− 3) B. (−3, 3) C. (3,− 3) D. (3, 3)
3. 若a>b,则下列结论一定成立的是( )
A. −2a<−2b B. a+5
A. 5 B. −5 C. ±5 D. −25
5. 下列命题中,为真命题的是( )
A. 相等的两个角为对顶角
B. 同旁内角互补
C. 在同一平面内,垂直于同一直线的两直线垂直
D. 在同一平面内,平行于同一直线的两直线平行
6. 向阳村购买玫瑰和芍药两种幼苗种植在景观大道两侧,已知购买2株玫瑰幼苗和3株芍药幼苗共需28元,购买5株玫瑰幼苗和6株芍药幼苗共需61元,若设每株玫瑰幼苗x元,每株芍药幼苗y元,则所列方程组正确的是( )
A. 3x+2y=286x+5y=61 B. 2x+3y=285x+6y=61 C. x3+y2=28x6+y5=61 D. x2+y3=28x5+y6=61
7. 实数m对应的点在数轴上的位置如图,则化简 (m−2)2+ (m−7)2的结果为( )
A. 2m−9 B. −5 C. 5 D. 9−2m
8. 如图,在下列选项中,不能判断DE//BC的是( )
A. ∠1=∠B
B. ∠2=∠3
C. ∠C+∠5+∠6=180°
D. ∠4=∠5
9. 已知x=2y=3是关于x,y的方程组mx+ny=23nx−my=−2的解,则5m+n的平方根为( )
A. −4和4 B. −5和5 C. − 13和 13 D. −2 7和2 7
10. 关于x的不等式组3x+2<2x−1x−1
第II卷(非选择题)
二、填空题(本大题共8小题,共32.0分)
11. 求值: 144= .
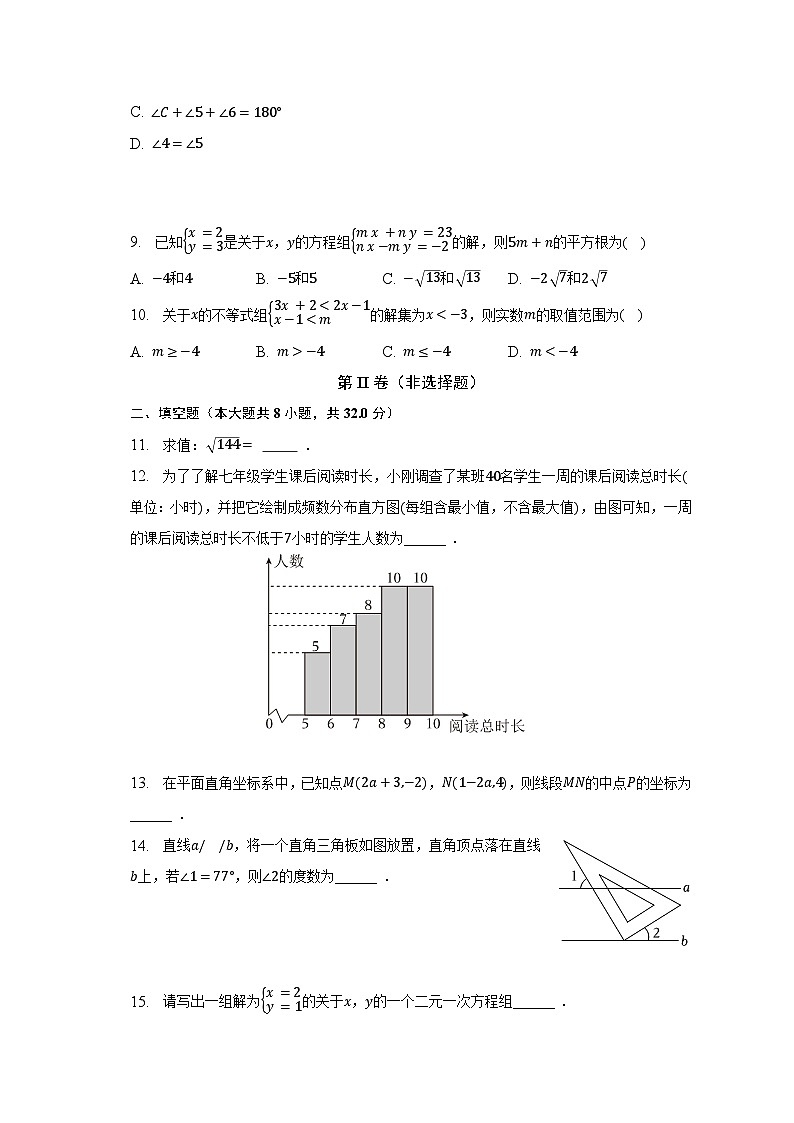
12. 为了了解七年级学生课后阅读时长,小刚调查了某班40名学生一周的课后阅读总时长(单位:小时),并把它绘制成频数分布直方图(每组含最小值,不含最大值),由图可知,一周的课后阅读总时长不低于7小时的学生人数为______ .
13. 在平面直角坐标系中,已知点M(2a+3,−2),N(1−2a,4),则线段MN的中点P的坐标为______ .
14. 直线a//b,将一个直角三角板如图放置,直角顶点落在直线b上,若∠1=77°,则∠2的度数为______ .
15. 请写出一组解为x=2y=1的关于x,y的一个二元一次方程组______ .
16. 如图,将△ABC沿射线BC平移3个单位后得到△DEF,连接AD,若AD=3EC,则BF的长为______
17. 若关于y的不等式组y−2≤14−3y2y+2>a−y,有5个整数解,则实数a的能取到的最小整数为______ .
18. 对于一个三位数M,若其个位上的数与百位上的数之和等于十位上的数,则称数M为“和悦数“.如:三位数583,∵5+3=8,∴583是“和悦数”;三位数678,∵6+8*7,∴678不是“和悦数”;则最小的“和悦数”为______ ;三位数M是“和悦数”,若M77为整数,则满足条件的M的最大值为______ .
三、解答题(本大题共8小题,共78.0分。解答应写出文字说明,证明过程或演算步骤)
19. (本小题8.0分)
计算:
(1) 6425×[(−2)2+1]+3−27+23× 2014;
(2) 16+ (−3)2+38− 50+|7−5 2|.
20. (本小题10.0分)
端午节是我国的传统节日,民间历来有吃粽子的习惯,端午节来临之际,某商场推出四种不同口味的粽子:原味(记为A),甜枣(记为B),腊肉(记为C),豆沙(记为D),为了解消费者对四种口味粽子的喜爱情况,在端午节前对购买不同口味粽子的消费者人数进行了调查统计,并将调查情况绘制成了如下两幅不完整的统计图:
根据以上信息回答下列问题:
(1)本次调查统计的总人数为______ .
(2)将条形统计图补充完整;
(3)经预测,端午节当日,有3000名消费者会在该商场购买粽子,请估计购买腊肉味粽子的人数;
(4)如果你是该商场负责人,你将如何安排四种口味粽子的货量,请结合数据说明你的理由.
21. (本小题10.0分)
如图,直线AB,CD,EF相交于点O,EF⊥CD,OG平分∠BOE.
(1)写出∠AOC的所有余角;
(2)写出∠AOE的邻补角;
(3)若∠DOG=30°,求∠BOD的度数.
22. (本小题10.0分)
(1)解方程组:3(x+y)−2(2x−y)=8,①8(x−y)−3(x+y)=−12,②
(2)解不等式组:x−3(x−1)≤4,①3x−15
在平面直角坐标系中,△ABC经过平移得到△AB′C′,△ABC与△ACB′C′的位置如图所示.
(1)分别写出点B,B′的坐标;
(2)请结合平移的相关知识说明△A′B′C′可由△ABC经过怎样的平移得到?
(3)点M(a+2,b−1)为△ABC内一点,其平移后的对应点为M′(9−b,2a+11),求实数a,b的值.
24. (本小题10.0分)
如图,点E,F分别在直线AB,CD上,连接AD,CE,BF,AD分别与CE,BF相交于点G,H,∠1=∠2,∠AEC=∠BFD.
(1)求证:BF//CE;
(2)求证:∠BAD=∠ADC.
25. (本小题10.0分)
每年五、六月份是我国冬小麦的收割时间.某农业合作社租用中型收割机和小型收割机进行冬小麦收割.已知1台中型收割机和3台小型收割机一天共能收割小麦430亩,1台中型收割机比1台小型收割机每天多收割70亩.
(1)求每台中型收割机和每台小型收割机平均每天各收割小麦多少亩?
(2)每台中型收割机和每台小型收割机每天的租用费用分别为1800元和1000元,该合作社种植了冬小麦5350亩,合作社计划租用两型收割机共8台,恰好用5天时间将小麦全部收割,要使租用收割机的总费用不超过65000元,试求有哪几种租用方案.
26. (本小题10.0分)
如图,直线MN//PQ,点A,B分别在直线MN,PQ上.
(1)如图1,点C在直线MN,PQ之间,求证:∠MAC+∠ACB+∠CBP=360°.
(2)如图2,点C在直线MN,PQ之间,连接AC,BC,∠ACB=45°,AD//BC,点E在线段BC上且满足∠CAE=3∠CAN,试判断∠DAE与∠CBP的数量关系,并证明你的结论;
(3)如图3,点C在直线MN上方,∠ACB=45°,AD//BC,点E在线段BC上且满足∠CAE=3∠CAN,请直接写出∠DAE,∠CBP,90°间的数量关系.
答案和解析
1.【答案】D
【解析】解:A.了解市场上奶茶的质量,适合进行抽样调查,故本选项不合题意;
B.了解一次性餐盒的卫生状况,适合进行抽样调查,故本选项不合题意;
C.了解某型号智能手表的电池寿命,适合进行抽样调查,故本选项不合题意;
D.了解一个班级的视力情况,适合进行全面调查,故本选项符合题意;
故选:D.
根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
2.【答案】C
【解析】解:第四象限中点的坐标特征P(x,y),x>0,y<0,
∵3>0,y<− 3.
故选:C.
利用各个象限中的坐标特征逐个判断即可.
本题考查各个象限中点的坐标特征,第四象限中点的坐标特征P(x,y),x>0,y<0是突破本题的关键.
3.【答案】A
【解析】解:∵a>b,
∴2a>2b,
∴−2a<−2b,
因此选项A符合题意;
∵a>b,
∴a+5>b+5,
因此选项B不符合题意;
由于a>b,若c<0时,则ac
因此选项C不符合题意;
∵a>b,
∴a−c>b−c,
因此选项D不符合题意;
故选:A.
根据不等式的性质逐项进行判断即可.
本题考查不等式的性质,掌握不等式的性质是正确解答的前提.
4.【答案】B
【解析】解:3−125=−5.
故选:B.
根据立方根的定义计算即可得解.
本题考查了立方根的定义,是基础题,熟记概念是解题的关键.
5.【答案】D
【解析】解:A:相等的两个角不一定有公共顶点,即相等的两个角不一定是对顶角,A不符合题意;
B:两直线平行才有同旁内角互补,B不符合题意;
C:同一平面内,垂直于同一直线的两直线平行,C不符合题意;
D:由平行线的传递性可知,D符合题意.
故选:D.
由对顶角的定义可判断A;
由平行线的性质可判断B;
由平行和垂直的性质可判断C,D.
本题主要考查了对顶角的定义、平行线的相关性质.本题的关键是熟练掌握定义和定理.
6.【答案】B
【解析】解:∵购买2株玫瑰幼苗和3株芍药幼苗共需28元,
∴2x+3y=28;
∵购买5株玫瑰幼苗和6株芍药幼苗共需61元,
∴5x+6y=61.
∴根据题意可列方程组2x+3y=285x+6y=61.
故选:B.
根据“购买2株玫瑰幼苗和3株芍药幼苗共需28元,购买5株玫瑰幼苗和6株芍药幼苗共需61元”,即可列出关于x,y的二元一次方程组,此题得解.
本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
7.【答案】C
【解析】解:由数轴可得3
原式=|m−2|+|m−7|
=m−2+7−m
=5,
故选:C.
由数轴可得3
8.【答案】D
【解析】解:A、∵∠1=∠B,
∴DE//BC,故此选项不符合题意;
B、∵∠2=∠3,
∴DE//BC,故此选项不符合题意;
C、∵∠C+∠5+∠6=180°,
∴DE//BC,故此选项不符合题意;
D、∵∠4=∠5,
∴DF//EC,故此选项符合题意;
故选:D.
直接利用平行线的判定定理分析得出答案.
此题主要考查了平行线的判定,正确掌握平行线的判定方法是解题关键.
9.【答案】B
【解析】解:∵x=2y=3是关于x,y的方程组mx+ny=23nx−my=−2的解,
∴2m+3n=23①2n−3m=−2②,
①−②得:5m+n=25,
∵52=25,(−5)2=25,
∴25的平方根为±5,
故选:B.
将x=2y=3代入原方程组,然后将两个方程相减求得5m+n的值,最后根据平方根的定义即可求得其答案.
本题考查二元一次方程组的解及平方根的定义,结合已知条件求得5m+n=25是解题的关键.
10.【答案】A
【解析】解:解不等式3x+2<2x−1,得x<−3,
解不等式x−1
解得m≥−4.
故选:A.
分别求出每一个不等式的解集,根据口诀:同小取小结合不等式组的解集可得m的值.
本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
11.【答案】12
【解析】解:∵12的平方等于144,
∴ 144=12.
故答案为:12.
如果一个非负数x的平方等于a,那么x是a的算术平方根,根据此定义即可解决问题.
本题比较容易,考查算术平方根的求法.要注意不要和平方根混淆而得出错误的结果±12.
12.【答案】28名
【解析】解:由图可知,一周的课后阅读总时长不低于7小时的学生人数为8+10+10=28(名),
故答案为:28名.
将第3、4、5组人数相加即可得出答案.
本题考查频数分布直方图,解答本题的关键是明确题意,利用数形结合的思想解答.
13.【答案】(2,1)
【解析】解:如图,作MC//x轴、NC//y轴,MC与NC相交于点C;点A、B分别为MC、NC的中点,连接PB、PA.
∴PA//NC,PB//MC,
∴PA⊥x轴,PB⊥y轴.
∴点A的横坐标等于点P的横坐标,点B的纵坐标等于点P的纵坐标.
点A的横坐标为2a+3+1−2a2=2,点B的纵坐标为−2+42=1.
∴P(2,1).
故答案为:(2,1).
作MC//x轴、NC//y轴,MC与NC相交于点C;点A、B分别为MC、NC的中点,连接PB、PA,利用三角形中位线定理即可求解.
本题考查坐标与图形的性质,用到三角形中位线定理.
14.【答案】13°
【解析】解:∵a//b,
∴∠1=∠3=77°,
∴∠2=90°−∠3=90°−77°=13°.
故答案为:13°.
先由余角的定义求出∠3的度数,再根据平行线的性质求出∠2的度数,即可得出结论.
本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.
15.【答案】x+y=3x−y=1(答案不唯一)
【解析】解:∵x=2,y=1,
∴x+y=2+1=3,x−y=2−1=1,
∴x=2y=1是二元一次方程组x+y=3x−y=1的解.
故答案为:x+y=3x−y=1(答案不唯一).
将x=2,y=1,分别代入x+y及x−y中,即可得出x=2y=1是二元一次方程组x+y=3x−y=1的解.
本题考查了二元一次方程组的解以及二元一次方程组的定义,牢记“一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解”是解题的关键.
16.【答案】7
【解析】解:∵△ABC沿射线BC平移3个单位得到△DEF,
∴AD=BE=CF=3,
∵AD=3EC,
∴EC=1,
∴BF=BE+CE+CF=3+1+3=7,
故答案为:7.
利用平移的性质得到AD=BE=CF=3,由AD=3EC可求BC,根据线段的和差求出BF即可.
本题考查了平移的性质:新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行(或共线)且相等.
17.【答案】−1
【解析】解:解不等式组y−2≤14−3y2y+2>a−y,得:a−23
∴整数解是4,3,2,1,0,
∴−1≤a−23<0,
解得:−1≤a<2,
∴实数a的最小整数解为−1.
故答案为:−1.
先求出不等式组的解集,根据已知得出关于a的不等式组,求出不等式组的解集,进而求解即可.
本题考查了解一元一次不等式组和不等式组的整数解,能得出关于a的不等式组是解此题的关键.
18.【答案】121 693
【解析】解:(1)设这个三位数M=abc−,
∵三位数M的个位上的数与百位上的数之和等于十位上的数,
即a+c=b,
∴当a=1,c=1时,b=2,M有最小值121,
(2)∵三位数M是“和悦数”,而M77为整数,
∴M77=abc−77=100a+10b+c77=100a+10(a+c)+c77=110a+11c77=10a+c7,
∵M77为整数,
∴(10a+c)被7整除,
∵M的取最大值,且a+c=b,
∴当b=9时,a=6,c=3,符合题意,
∴M的最大值为693.
故答案为:121,693.
(1)根据题意可直接得出答案;
(2)由题意化简M77,得到(10a+c)被7整除,从而得出符合要求的M的最大值.
本题主要考查了有理数的运算,列代数式,有理数的整除特性.本题是阅读型题目,准确理解题干中的定义和公式并熟练运用是解题的关键.
19.【答案】解:(1) 6425×[(−2)2+1]+3−27+23× 2014
=85×(4+1)−3+23× 814
=85×5−3+23×92
=8−3+3
=8;
(2) 16+ (−3)2+38− 50+|7−5 2|
=4+3+2−5 2+5 2−7
=2.
【解析】(1)先把被开方数2014化为假分数,然后利用算术平方根的定义、立方根的定义进行化简,最后按照实数的运算法则计算即可;
(2)先估算7与5 2的大小关系,然后按照绝对值的意义去掉绝对值符号,其它的利用算术平方根的定义、立方根的定义进行化简,即可得出结果.
本题考查了实数的运算,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握算术平方根、立方根、绝对值等考点的运算.
20.【答案】200
【解析】解:(1)本次调查统计的总人数为:80÷40%=200(人),
故答案为:200;
(2)C的人数为:200−80−40−20=60(人),
补全条形统计图如下:
(3)3000×60200=900(人),
答:计购买腊肉味粽子的人数大约为900人;
(4)因为A、B、C、D四种口味粽子的销量比为4:2:3:1,所以多进A种货,少进D种货,B、C种适量进货即可.
(1)用A的人数除以40%可得答案;
(2)先求出喜欢吃C种粽子的人数,补全条形统计图即可;
(3)购买腊肉味粽子的人数=总人数×爱吃C种粽子的百分比;
(4)估计四种口味粽子所占比例解答即可.
本题主要考查了条形统计图,用样本估计总体与扇形统计图,解题的关键是读懂统计图,从统计图中获得准确的信息.
21.【答案】解:(1)∵EF⊥CD,
∴∠COE=∠COF=∠DOE=90°,
∴∠AOC+∠AOE=∠AOC+∠BOF=90°,
∴∠AOC的所有余角:∠AOE、∠BOF;
(2)∵∠BOE+∠AOE=∠AOF+∠AOE=180°,
∴∠AOE的所有补角:∠BOE、∠AOF;
(3)∴∠DOE=90°,∠DOG=30°,
∴∠EOG=60°,
∵OG平分∠BOE,
∴∠BOG=∠EOG=60°,
∴∠BOD=60°−30°=30°.
【解析】(1)根据余角的定义即可判断;
(2)根据邻补角的定义即可判断;
(3)由角平分线的定义可求∠BOG=60°,即可求出答案.
本题考查垂线,余角,角平分线的定义,邻补角的概念,关键是掌握垂线,余角,邻补角的定义,角平分线的定义.
22.【答案】解:(1)由①得x−5y=−8③,
由②得5x−11y=−12④,
③×5−④得−14y=−28,
解得y=2,
把y=2代入③得x−10=−8,
解得x=2,
所以原方程组的解为x=2y=2;
(2)解不等式①得x≤−12,
解不等式②得x<7,
所以不等式组的解集为−12≤x<7.
【解析】(1)先把方程①②变形得到x−5y=−8③和5x−11y=−12④,再利用加减消元法求出x,然后利用代入法求出x,从而得到方程组的解;
(2)分别解两个不等式得到x≥−12和x<7,然后利用大小小大中间找确定不等式组的解集.
本题考查了解一元一次不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分.也考查了解二元一次方程组.
23.【答案】解:(1)点B的坐标为(−5,2),点B′的坐标为(3,−3),
(2)△A′B′C′可由△ABC向右平移8个长度单位,再向下平移5个长度单位得到;
(3)∵点M(a+2,b−1)和点M′(9−b,2a+11)是对应点,
∴a+2+8=9−bb−1−5=2a+11,解得:a=−6b=5.
∴a=−6,b=5.
【解析】(1)观察图形中点B和点B′的位置即可得得出其坐标;
(2)观察图形中△ABC和△A′B′C′的位置的变换可得出答案;
(3)由(2)可知:将△ABC向右平移8个长度单位,再向下平移5个长度单位得到△A′B′C′,由于点M(a+2,b−1)平移后的对应点M′(9−b,2a+11),可得出方程组a+2+8=9−bb−1−5=2a+11,解此方程组可求出a,b.
此题主要考查了点的坐标的平移,解答此题的关键是熟练掌握点的坐标的平移规律.
24.【答案】证明:(1)∵∠1=∠2,∠2=∠AHB,
∴∠1=∠AHB,
∴BF//CE(同位角相等,两直线平行),
(2)由(1)可得出∠AEC=∠B,
∵∠AEC=∠BFD,
∴∠B=∠BFD,
∴AB//CD(内错角相等,两直线平行),
∴∠BAD=∠ADC.
【解析】(1)由∠1=∠2,∠2=∠AHB,可得BF//CE,
(2)由(1)可得出∠AEC=∠B.再结合∠AEC=∠BFD可得∠B=∠BFD,即可得出AB//CD,从而得出∠BAD=∠ADC.
本题考查平行线的性质和判断,熟练掌握平行线的性质和判断是解题关键.
25.【答案】解:(1)设每台中型收割机平均每天收割小麦x亩,每台小型收割机平均每天收割小麦y亩,
根据题意得:x+3y=430x−y=70,
解得:x=160y=90.
答:每台中型收割机平均每天收割小麦160亩,每台小型收割机平均每天收割小麦90亩;
(2)设租用m台中型收割机,则租用(8−m)台小型收割机,
根据题意得:160×5m+90×5(8−m)≥53501800×5m+1000×5(8−m)≤65000,
解得:5≤m≤254,
又∵m为正整数,
∴m可以为5,6,
∴共有2种租用方案,
方案1:租用5台中型收割机,3台小型收割机;
方案2:租用6台中型收割机,2台小型收割机.
【解析】(1)设每台中型收割机平均每天收割小麦x亩,每台小型收割机平均每天收割小麦y亩,根据“1台中型收割机和3台小型收割机一天共能收割小麦430亩,1台中型收割机比1台小型收割机每天多收割70亩”,可列出关于x,y的二元一次方程组,解之即可得出结论;
(2)设租用m台中型收割机,则租用(8−m)台小型收割机,根据“恰好用5天时间将小麦全部收割,且租用收割机的总费用不超过65000元”,可列出关于m的一元一次不等式组,解之可得出m的取值范围,再结合m为正整数,即可得出各租用方案.
本题考查了二元一次方程组的应用以及一元一次不等式组的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式组.
26.【答案】(1)证明:过点C作CH//MN,
∵MN//PQ,
∴MN//MN//PQ,
∴∠MAC+∠ACH=180°,∠BCH+∠CBP=180°,
∴∠MAC+∠ACH+∠BCH+∠CBP=360°,
即:∠MAC+ACB+∠CBP=360°.
(2)解:∠DAE与∠CBP的数量关系是:∠DAE+3∠CBP=540°.
证明如下:
设∠CAN=α,∠CBP=β,
∴∠CAE=3∠CAN=3α,∠MAC=180°−∠CAN=180°−α,
∵∠ACB=45°,
∴∠AEC=180°−∠ACB−∠CAE=180°−45°−3α=135°−3α,
∵AD//PQ,
由(1)可知:∠MAC+∠ACB+∠CBP=360°,
∴180°−α+45°+β=360°,
∴α=β−135°,
∵AD//BC,
∴∠DAE=∠AEC=135°−3α=135°−3(β−135°)=540°−3β,
∴∠DAE+3β=540°,
即:∠DAE+3∠CBP=540°,
(3)解:∠DAE,∠CBP,90°间的数量关系是:3∠CBP−∠DAE=3×90°.
理由如下:
设∠CAN=α,∠CBP=β,
∴∠CAE=3∠CAN=3α,
∴∠NAE=∠CAE−∠CAN=2α,
∴∠MAE=180°−∠NAE=180°−2α,
∵∠ACB=45°,
∴∠AEB=∠CAE+∠ACB=3α+45°,
由(1)可知:∠MAE+∠AEB+∠CBP=360°,
∴180°−2α+3α+45°+β=360°,
∴α=135°−β,
∵AD//BC,
∴∠DAE+∠AEB=180°,
∴∠DAE=180°−∠AEB=180°−(3α+45°)=135°−3α,
又∵α=135°−β,
∴∠DAE=135°−3(135°−β)=3β−270°,
∴3β−∠DAE=270°,
即:3∠CBP−∠DAE=3×90°.
【解析】(1)过点C作CH//MN,由平行线的性质得∠MAC+∠ACH=180°,∠BCH+∠CBP=180°,据此可得出结论;
(2)设∠CAN=α,∠CBP=β,则∠CAE=3∠CAN=3α,∠MAC=180°−α,由三角形的内角和定理得∠AEC=135°−3α,然后由(1)的结论∠MAC+∠ACB+∠CBP=360°,即α=β−135°,最后由AD//BC得∠DAE=∠AEC=135°−3α,将α=β−135°代入得∠DAE+3β=540°,据此可得出∠DAE与∠CBP的数量关系;
(3)设∠CAN=α,∠CBP=β,则∠CAE=3∠CAN=3α,∠NAE=2α,∠MAE=180°−2α,由(1)的结论得∠MAE+∠AEB+∠CBP=360°,即α=135°−β,再由AD//BC得∠DAE+∠AEB=180°,进而得∠DAE=135°−3α,将α=135°−β代入得∠DAE=3β−270°,据此可得∠DAE,∠CBP,90°间的数量关系.
此题主要考查了平行线的性质,解答此题的关键是准确识图,熟练掌握平行线的性质:两直线平⇔同位角相等;两直线平行内错角相等;两直线平行⇔同旁内角互补.
2023-2024学年重庆市合川区七年级(上)期末数学试卷(含详细答案解析): 这是一份2023-2024学年重庆市合川区七年级(上)期末数学试卷(含详细答案解析),共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年重庆市合川区七年级(上)期末数学试卷(含解析): 这是一份2023-2024学年重庆市合川区七年级(上)期末数学试卷(含解析),共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年重庆市合川中学七年级(上)期末数学试卷(含解析): 这是一份2022-2023学年重庆市合川中学七年级(上)期末数学试卷(含解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












