

2022-2023学年安徽省蚌埠市怀远实验中学七年级(下)期末数学试卷(含解析)
展开2022-2023学年安徽省蚌埠市怀远实验中学七年级(下)期末数学试卷
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列实数 5,0,3−64,π,其中,无理数共有( )
A. 1个 B. 2个 C. 3个 D. 4个
2. 25的平方根是( )
A. 5 B. ±5 C. 5 D. ± 5
3. 数轴上表示1, 2的点分别为A,B,点A是BC的中点,则点C所表示的数是( )
A. 2−1 B. 1− 2 C. 2− 2 D. 2−2
4. 下列运算中,计算正确的是( )
A. a3+a3=a6 B. (2a2)3=6a6 C. a2⋅a3=a6 D. (2a3)2=4a6
5. 若4x2+mx+9是完全平方式,则m的值为( )
A. ±16 B. ±12 C. 12 D. −12
6. 如果把分式3xx2+y2中的x和y都扩大3倍,那么分式的值( )
A. 扩大9倍 B. 扩大3倍 C. 不变 D. 缩小3倍
7. 方程x−2x−4−3=2x−4有增根,则增根是( )
A. x=6 B. x=5 C. x=4 D. x=3
8. 关于x的不等式组2x+13≥x−12x>a+1有且只有2个整数解,则符合要求的所有整数a的和为( )
A. −7 B. −3 C. 0 D. 7
9. 如图,以数轴的单位长度线段为边长作一个正方形,以表示数1的点为圆心,正方形对角线长为半径画半圆,交数轴于点A、B,则点A、B表示的数分别是( )
A. − 2, 2 B. 2−1, 2+1
C. 1− 2,1+ 2 D. 1− 2, 2
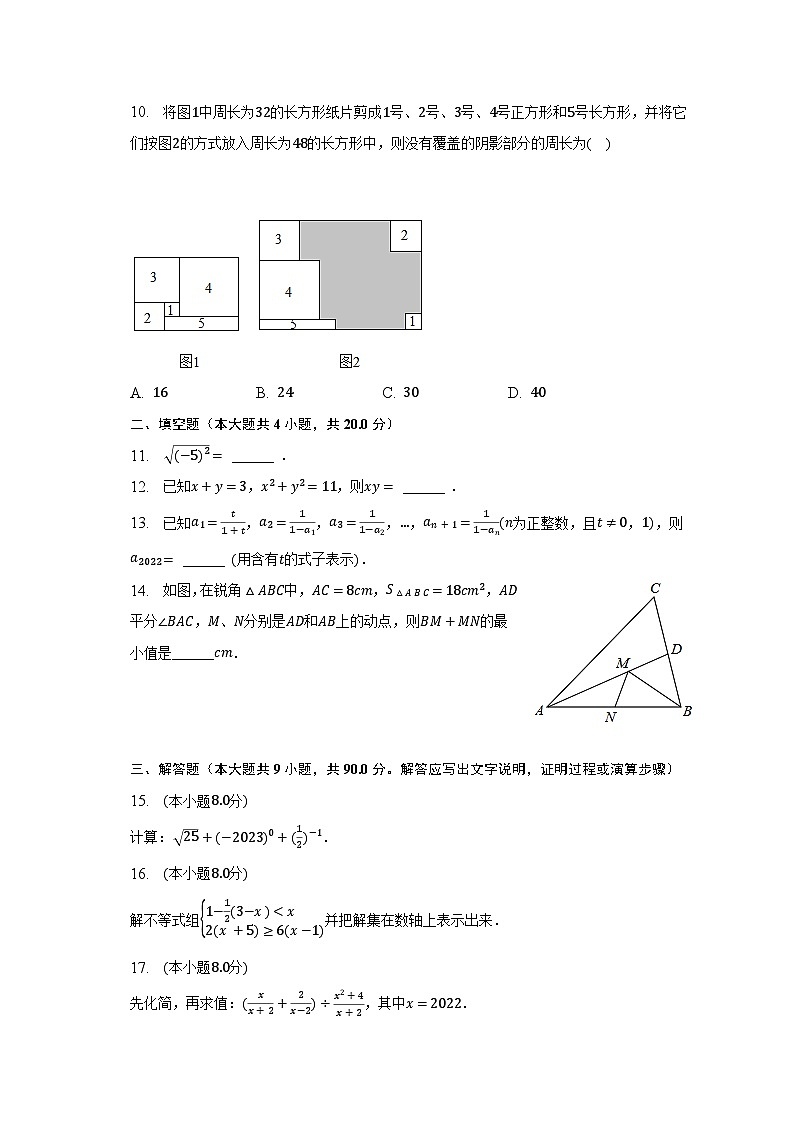
10. 将图1中周长为32的长方形纸片剪成1号、2号、3号、4号正方形和5号长方形,并将它们按图2的方式放入周长为48的长方形中,则没有覆盖的阴影部分的周长为( )
A. 16 B. 24 C. 30 D. 40
二、填空题(本大题共4小题,共20.0分)
11. (−5)2= ______ .
12. 已知x+y=3,x2+y2=11,则xy= ______ .
13. 已知a1=t1+t,a2=11−a1,a3=11−a2,…,an+1=11−an(n为正整数,且t≠0,1),则a2022= ______ (用含有t的式子表示).
14. 如图,在锐角△ABC中,AC=8cm,S△ABC=18cm2,AD平分∠BAC,M、N分别是AD和AB上的动点,则BM+MN的最小值是______cm.
三、解答题(本大题共9小题,共90.0分。解答应写出文字说明,证明过程或演算步骤)
15. (本小题8.0分)
计算: 25+(−2023)0+(12)−1.
16. (本小题8.0分)
解不等式组1−12(3−x)
先化简,再求值:(xx+2+2x−2)÷x2+4x+2,其中x=2022.
18. (本小题8.0分)
某校需购买A、B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍.设购买A种奖品m件,求出自变量m的取值范围.
19. (本小题10.0分)
如图,已知A、B、C、D是正方形网格纸上的四个格点.
(1)根据要求在网格中画图并标注相关字母:
①画线段AB;
②画直线AC;
③过点B画AD的平行线BE;
④过点D画AC的垂线,垂足为F.
(2)点D与直线AC上各点连接的所有线段中,最短线段是______ ,依据是______ .
20. (本小题10.0分)
实践与探究,如图1,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的公式是______ (请选择正确的一个).
A.a2+ab=a(a+b) B.a2−b2=(a−b)(a+b) C.a2−2ab+b2=(a−b)2
(2)请应用上面的公式完成下列各题:①已知4a2−b2=24,2a+b=6,则2a−b= ______ ;②计算:82−72+62−52+42−32+22−1;③计算:(2n)2−(2n−1)2+(2n−2)2−(2n−3)2+⋯+42−32+22−1(n≥1).
21. (本小题12.0分)
如图,AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°.
试说明:∠GDC=∠B,在下列解答中,填空(理由或数学式).
解:∵AD⊥BC,EF⊥BC(已知),
∴∠ADB=∠EFB=90°(______ ).
∴EF//AD(______ ).
∴ ______ +∠2=180°(______ ).
又∵∠2+∠3=180°(已知),
∴∠1=∠3(______ ).
∴AB// ______ (______ ).
∴∠GDC=∠B(______ ).
22. (本小题12.0分)
某学校2021年在某商场购买甲、乙两种不同的足球,购买甲种足球共花费4000元,购买乙种足球共花费2800元,购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元;
(1)求购买一个甲种足球、一个乙种足球各需多少元;
(2)2022年这所学校决定再次购买甲、乙两种足球共50个.恰逢该商场对两种足球的售价进行调整,甲种足球售价比第一次购买时提高了10%,乙种足球售价比第一次购买时降低了10%.如果此次购买甲、乙两种足球的总费用不超过2910元,那么这所学校最多可购买多少个乙种足球?
23. (本小题14.0分)
如图1,已知两条直线AB,CD被直线EF所截,分别交于点E,点F,EM平分∠AEF交CD于点M,且∠FEM=∠FME.
(1)判断直线AB与直线CD是否平行,并说明理由;
(2)如图2,点G是射线MD上一动点(不与点M,F重合),EH平分∠FEG交CD于点H,过点H作HN⊥EM于点N,设∠EHN=α,∠EGF=β.
①当点G在点F的右侧时,若α=30°,求β的度数;
②当点G在运动过程中,α和β之间有怎样的数量关系?请写出你的猜想,并加以证明.
答案和解析
1.【答案】B
【解析】解:3−64=−4,
无理数有: 5,π,共2个,
故选:B.
根据无理数的定义解答即可.
此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样无限不循环小数.
2.【答案】B
【解析】解;25的平方根是±5,
故选:B.
根据开平方的意义,可得答案.
本题考查了平方根,一个正数有两个平方根,它们互为相反数.
3.【答案】C
【解析】解:∵数轴上1, 2的对应点分别是点A和点B,
∴AB= 2−1,
∵A是线段BC的中点,
∴CA=AB,
∴点C的坐标为:1−( 2−1)=2− 2.
故选:C.
首先根据数轴上1, 2的对应点分别是点A和点B,可以求出线段AB的长度,然后根据中点的性质即可解答.
本题考查了实数与数轴,用到的知识点为:求数轴上两点间的距离就让右边的数减去左边的数.知道两点间的距离,求较小的数,就用较大的数减去两点间的距离.
4.【答案】D
【解析】解:A.a3+a3=2a3,故本选项不合题意;
B.(2a2)3=8a6,故本选项不合题意;
C.a2⋅a3=a5,故本选项不合题意;
D.(2a3)2=4a6,故本选项符合题意.
故选:D.
分别根据合并同类项法则,幂的乘方与积的乘方运算法则,同底数幂的乘法法则逐一判断即可.
本题主要考查了合并同类项,同底数幂的乘法以及幂的乘方与积的乘方,熟记幂的运算法则是解答本题的关键.
5.【答案】B
【解析】解:∵4x2+mx+9是完全平方式,
∴4x2+mx+9=(2x±3)2=4x2±12x+9,
∴m=±12,
m=±12.
故选:B.
这里首末两项是2x和3这两个数的平方,那么中间一项为加上或减去2x和3积的2倍.
此题主要考查了完全平方公式的应用,两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式.注意积的2倍的符号,避免漏解.
6.【答案】D
【解析】解:分式3xx2+y2中的x和y都扩大3倍,得
3×3x(3x)2+(3y)2=9x9x2+9y2=13×3xx2+y2
所以分式的值缩小了3倍;
故选:D.
根据分式的性质即可得出答案.
本题考查了分式的基本性质,把x,y换成3x,3y是解题的关键.
7.【答案】C
【解析】解:∵分式方程有增根,
∴最简公分母x−4=0,
∴x=4,即分式方程增根为x=4,
故选:C.
根据增根的定义可知,最简公分母为零的未知数的值是增根,根据分式方程判断出最简公分母,令最简公分母为零即可求出x的值.
此题考查了分式方程的求解.注意增根形成的原因:最简公分母为零.
8.【答案】D
【解析】解:2x+13≥x−1①2x>a+1②,
解不等式①,得x≤4,
解不等式②,得x>a+12,
所以不等式组的解集为:a+12
∴2≤a+12<3,
解得3≤a<5,
∵a为整数,
∴a为3,4,
∴和为3+4=7,
故选:D.
分别表示出不等式组两不等式的解集,找出两解集的公共部分表示出不等式组的解集,由不等式组有且只有2个整数解确定出a的范围,进而求出整数a的值,求出和即可.
此题考查了一元一次不等式组的整数解,熟练掌握不等式组的解法是解本题的关键.
9.【答案】C
【解析】解:数轴上正方形的对角线长为: 12+12= 2,由图中可知1和A之间的距离为 2.
∴点A表示的数是1− 2;点B表示的数为1+ 2.
故选:C.
先根据勾股定理求出正方形的对角线长,再根据两点间的距离公式为:两点间的距离=较大的数−较小的数,便可求出1和A之间的距离,进而可求出点A表示的数.
本题考查的是勾股定理及两点间的距离公式,本题需注意:知道数轴上两点间的距离,求较小的数,就用较大的数减去两点间的距离.
10.【答案】D
【解析】解:设1号正方形的边长为x,2号正方形的边长为y,
则3号正方形的边长为x+y,4号正方形的边长为2x+y,
5号长方形的长为3x+y,宽为y−x,
由图1中长方形的周长为32,可得,y+2 (x+y)+(2x+y)=16,
解得,x+y=4,
如图,图2中长方形的周长为48,
∴AB+2 (x+y)+2x+y+y−x=24,
∴AB=24−3x−4y,
根据题意得:没有覆盖的阴影部分的周长为四边形ABCD的周长,
∴2 (AB+AD)
=2(24−3x−4y+x+y+2x+y+y−x)
=2 (24−x−y)
=48−2 (x+y)
=48−8=40,
故选:D.
设1号正方形的边长为x,2号正方形的边长为y,则3号正方形的边长为x+y,4号正方形的边长为2x+y,5号长方形的长为3x+y,宽为y−x,根据图1中长方形的周长为32,求得x+y=4,根据图2中长方形的周长为48,求得AB=24−3x−4y,没有覆盖的阴影部分的周长为四边形ABCD的周长=2(AB+AD),计算即可得到答案.
此题考查整式加减的应用,解题的关键是设出未知数,列代数式表示各线段进而解决问题.
11.【答案】5
【解析】解: (−5)2=|−5|=5,
故答案为:5.
a2=|a|,据此即可求得答案.
本题考查二次根式的性质,熟练掌握其性质是解题的关键.
12.【答案】−1
【解析】解:∵x+y=3,
∴(x+y)2=9,
∴x2+y2+2xy=9
∵x2+y2=11,
∴11+2xy=9,
∴xy=−1.
故答案为:−1.
把x+y=3两边平方,然后利用完全平方公式求解即可.
本题考查了完全平方公式:(a±b)2=a2±2ab+b2.可巧记为:“首平方,末平方,首末两倍中间放”.
13.【答案】−1t
【解析】解:∵a1=t1+t,
a2=11−t1+t=t+1,
a3=11−(t+1)=−1t,
a4=11−(−1t)=t1+t,
∴结果每3个一循环,
∵2022=3×674,
∴a2022=−1t.
故答案为:−1t.
根据题意求出a1,a2,a3,a4,并从中找出规律即可求出答案.
本题考查了数字类规律探究,以及分式的计算,解题的关键是正确找出题中的规律.
14.【答案】92
【解析】解:作N关于AD的对称点为R,作AC边上的高BE(E在AC上),
∵AD平分∠CAB,△ABC为锐角三角形,
∴R必在AC上,
∵N关于AD的对称点为R,
∴MR=MN,
∴BM+MN=BM+MR,
即BM+MN=BR≥BE(垂线段最短),
∵△ABC的面积是18cm2,AC=8cm,
∴12×8×BE=18,
∴BE=92cm,
即BM+MN的最小值为92cm.
故答案为:92.
根据题意画出符合条件的图形,作N关于AD的对称点为R,作AC边上的高BE(E在AC上),求出BM+MN=BR,根据垂线段最短得出BM+MN≥BE,求出BE即可得出BM+MN的最小值.
本题考查了平面展开−最短路线问题,关键是画出符合条件的图形,题目具有一定的代表性,是一道比较好的题目.
15.【答案】解:原式=5+1+2=8.
【解析】由算术平方根性质解得 25=5,由a0=1(a≠0)解得(−2023)0=1,(12)−1=112=2据此解题.
本题考查实数的混合运算,涉及算术平方根、零指数幂、负整数指数幂等,是重要考点,难度较易,掌握相关知识是解题关键.
16.【答案】解:1−12(3−x)
解不等式②得,x≤4,
把不等式的解集表示在数轴上,
∴原不等式组的解集是−1
此题主要考查了一元一次不等式组,熟练掌握一元一次不等式组的解法是解题的关键.
17.【答案】解:原式=[x(x−2)(x+2)(x−2)+2(x+2)(x+2)(x−2)]÷x2+4x+2=x2+4(x+2)(x−2)⋅x+2x2+4=1x−2;
当x=2022时,原式=12022−2=12020.
【解析】先对分式进行化简,然后代值求解即可.
本题主要考查分式的化简求值,熟练掌握分式的运算是解题的关键.
18.【答案】解:(1)设A种奖品的单价是x元,B种奖品的单价是y元,
依题意得:3x+2y=605x+3y=95,
解得:x=10y=15.
答:A种奖品的单价是10元,B种奖品的单价是15元.
(2)若购买A种奖品m件,则购买B种奖品(100−m)件,
依题意得:m≤3(100−m)10m+15(100−m)≤1150,
解得:70≤m≤75.
答:自变量m的取值范围为70≤m≤75.
【解析】(1)设A种奖品的单价是x元,B种奖品的单价是y元,根据“若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元”,即可得出关于x,y的二元一次方程组,解之即可得出A、B两种奖品的单价;
(2)若购买A种奖品m件,则购买B种奖品(100−m)件,根据“购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍”,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围.
本题考查了二元一次方程组的应用、一元一次不等式组的应用以及函数自变量的取值范围,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式组.
19.【答案】DF 垂线段最短
【解析】解:(1)如图:
①线段AB即为所求;②直线AC即为所求;③BE即为所求;④点F即为所求;
(2)根据连接直线外一点与直线上各点的所有线段中,DF最短,理由是垂线段最短;
∵DF⊥AC,
∴DF最短;
(1)根据线段的定义,直线的定义,平行线的作法,垂线的作法作图即可;
(2)根据垂线段的性质判断即可.
本题考查了线段、直线、平行线、垂线的作法,垂线段的性质;掌握利用直尺和三角板作图的步骤是解题关键.
20.【答案】B 4
【解析】解:(1)图一中的阴影部分面积为:a2−b2,
图二中阴影部分面积为:(a+b)(a−b),
而这两者面积相等,所以有:a2−b2=(a+b)(a−b).
故选:B.
(2)①4a2−b2=(2a+b)(2a−b)=24,
又2a+b=6,
∴2a−b=4.
②82−72+62−52+42−32+22−1
=(8+7)(8−7)+(6+5)(6−5)+(4+3)(4−3)+(2+1)(2−1)
=8+7+6+5+4+3+2+1
=4×9
=36.
③(2n)2−(2n−1)2+(2n−2)2−(2n−3)2+⋯+42−32+22−1(n≥1)
=(2n+2n−1)(2n−2n+1)+(2n−2+2n−3)(2n−2+2n+3)+……+(4+3)(4−3)+(2+1)(2−1)=2n+2n−1+2n−2+2n−3+⋯+4+3+2+1
=(2n+1)2n2
=2n2+n.
故答案为:B,4.
(1)根据阴影部分写出两个图形中阴影部分面积的代数式,再得出二者相等的结论;
(2)使用(1)得出的公式对本题中的平方差进行因式分解即可求得结果.
本题考查平方差公式的证明与使用,考查求和公式,掌握这些是本题关键.
21.【答案】垂直的定义 同位角相等两直线平行 ∠1 两直线平行同旁内角互补 同角的补角相等 DG 内错角相等两直线平行 两直线平行同位角相等
【解析】解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90°(垂直的定义),
∴EF//AD (同位角相等两直线平行),
∴∠1+∠2=180°(两直线平行同旁内角互补),
又∵∠2+∠3=180°(已知),
∴∠1=∠3 (同角的补角相等),
∴AB//DG(内错角相等两直线平行),
∴∠GDC=∠B (两直线平行同位角相等).
故答案为:垂直的定义,同位角相等两直线平行,∠1,两直线平行同旁内角互补,同角的补角相等,DG,内错角相等两直线平行,两直线平行同位角相等.
根据平行线的判定和性质,垂直的定义,同角的补角相等知识一一判断即可.
本题考查平行线的判定和性质,解题的关键是熟练掌握基本知识,属于中考常考题型.
22.【答案】解:(1)设甲种足球每个x元,则乙种足球每个(x+20)元,
由题意得:4000x=2×2800x+20,
解得:x=50,
经检验,x=50是原方程的解,
∴50+20=70(元).
答:一个甲种足球需50元,一个乙种足球需70元.
(2)设购买乙种足球m个,50×1.1=55,70×0.9=63,
由题意得:55(50−m)+63m≤2910,
m≤20.
答:这所学校最多可购买20个乙种足球.
【解析】(1)设购买一个甲种足球需要x元,则购买一个乙种篮球需要(x+20)元,根据数量=总价÷单价结合购买甲种足球数量是购买乙种足球数量的2倍,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设可购买m个乙种足球,则购买(50−m)个甲种足球,根据总价=单价×数量结合此次购买甲、乙两种足球的总费用不超过2910元,即可得出关于m的一元一次不等式,解之取其中的最大值即可得出结论.
本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)根据各数量之间的关系,正确列出一元一次不等式.
23.【答案】解:(1)结论:AB//CD.
理由:如图1中,
∵EM平分∠AEF交CD于点M,
∴∠AEM=∠MEF,
∵∠FEM=∠FME.
∴∠AEM=∠FME,
∴AB//CD.
(2)①如图2中,
∵HN⊥EM,
∴∠HNE=90°,
∵α=30°,
∴∠EHN=90°−∠HEN=30°.
∴∠HEN=60°,
∵EH平分∠FEG,
∴∠HEF=∠HEG,
∵∠AEM=∠EMF,
∴∠HEN=12∠FEG+12∠AEF=12∠AEG=60°,
∴∠AEG=120°,则∠GEB=60°,
∵AB//CD,
∴∠BEG=∠EGH=β=60°;
②猜想:α=12β或α=90°−12β
理由:1)当点G在F的右侧时,
∵AB//CD,
∴∠BEG=∠EGH=β,
∴∠AEG=180°−β,
∵∠AEM=∠EMF,∠HEF=∠HEG,
∴∠HEN=∠MEF+∠HEF=12∠AEG=90°−12β,
∵HN⊥EM,
∴∠HNE=90°,
∴α=∠EHN=90°−∠HEN=12β.
(2)当点G在F的左侧时,
∵AB//CD,
∴∠BEG=180°−∠EGH=180°−β,∠AEG=∠EGH=β,
∵∠AEM=∠EMF,∠HEF=∠HEG,
∴∠HEN=∠MEF−∠HEF12(∠AEF−∠FEG)=12∠AEG=12β,
∵HN⊥EM,
∴∠HNE=90°,
∴α=∠EHN=90°−∠HEN=90°−12β.
综上所述,α=12β或α=90°−12β.
【解析】(1)根据角平分线的性质及等量代换证明∠AEM=∠FME即可.
(2)①根据三角形内角和定理得出∠HEN=60°,根据角平分线的定义∠HEN=12∠FEG+12∠AEF=60°,利用平角的定义求出∠GEB的度数,根据平行线的性质求∠BEG,即可解决问题.
②结论:α=12β.根据平行线的性质求∠BEG,利用平角的定义表示∠AEG的度数,根据角平分线的定义表示∠HEN即可解决问题.
本题考查三角形的内角和定理,平行线的性质,角平分线的定义等知识,掌握角平分线的定义以及平行线的性质解题的关键.
2022-2023学年安徽省蚌埠市怀远县七年级(下)期末数学试卷(含解析): 这是一份2022-2023学年安徽省蚌埠市怀远县七年级(下)期末数学试卷(含解析),共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
安徽省蚌埠市怀远县怀远实验中学2022-2023学年七年级下学期期末数学试卷(含答案): 这是一份安徽省蚌埠市怀远县怀远实验中学2022-2023学年七年级下学期期末数学试卷(含答案),共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中数学北京课改版七年级下册7.2 实验测试题: 这是一份初中数学北京课改版七年级下册7.2 实验测试题,共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












