2023年中考数学 章节专项练习26 反证法、命题与定理

这是一份2023年中考数学 章节专项练习26 反证法、命题与定理，共2页。试卷主要包含了 下列命题是真命题的是等内容，欢迎下载使用。
一、选择题1.（2019湖南岳阳，7，3分）下列命题是假命题的是（    ）A．平行四边形既是轴对称图形，又是中心对称图形B．同角（或等角）的余角相等C．线段垂直平分线上的点到线段两端的距离相等D．正方形的对角线相等，且互相垂直平分【答案】A【解析】平行四边形一定是中心对称图形，但不一定是轴对称图形，选项A是假命题；故选择A．【知识点】命题 2. (2019四川巴中,6,4分)下列命题是真命题的是(    )A.对角线相等的四边形是矩形     B.对角线互相垂直的四边形是矩形    C.对角线互相垂直的矩形是正方形    D.四边相等的平行四边形是正方形【答案】C【解析】对角线相等的平行四边形是矩形,故A,B均错误;对角线互相垂直的矩形是正方形,C正确;四边相等的平行四边形是菱形,故D错误;故选C.【知识点】矩形的判定,正方形的判定二、填空题1.（2019安徽省，12，5分）命题“如果，那么，互为相反数”的逆命题为             ．【答案】如果，互为相反数，那么．【解析】解：命题“如果，那么，互为相反数”的逆命题为：如果，互为相反数，那么；故答案为：如果，互为相反数，那么．【知识点】命题与定理三、解答题1.(2019浙江台州,22,12分)我们知道,各个角都相等,各条边都相等的多边形叫做正多边形.对一个各条边都相等的凸多边形(边数大于3),可以由若干条对角线相等判定它是正多边形.例如,各条边都相等的凸四边形,若两条对角线相等,则这个四边形是正方形.(1)已知凸五边形ABCDE的各条边都相等.①如图1,若AC＝AD＝BE＝BD＝CE,求证:五边形ABCDE是正五边形;②如图2,若AC＝BE＝CE,请判断五边形ABCDE是不是正五边形,并说明理由;(2)判断下列命题的真假.(在括号内填写"真"或"假")如图3,已知凸六边形ABCDEF的各条边都相等.①若AC＝CE＝EA,则六边形ABCDE是正六边形;(    )②若AD＝BE＝CF,则六边形ABCDE是正六边形;( 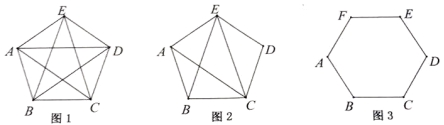   )【思路分析】(1)根据定义,利用全等,得到五个内角相等,则可证明其为正五边形;(2)根据已知条件,设法证明6个内奸相等,无法证明,故两个命题均为假命题.【解题过程】(1)①在△EAD和△ABE中,AB＝EA,AE＝ED,BE＝AD,∴△EAD≌△ABE,同理可得△EAD≌△ABE≌△BCA≌△CDB≌△DEC,∴∠ABC＝∠BCD＝∠CDE＝∠DEA＝∠EAB,∴五边形ABCDE是正五边形;②∵AC＝BE＝CE,AB＝BC＝CD＝DE＝EA,∴△ABC≌△EAB≌△DEC,∴设∠DCE＝∠ABE＝∠BCA＝x,易得△ACE≌△BEC,∴设∠ACE＝∠BEC＝y,∵EB＝EC,∴∠EBC＝∠ECB＝x+y,∴∠AED＝2x+y,∠BCD＝2x+y,∵∠ABC＝2x+y,∴∠ABC＝∠BCD＝∠CDE＝∠DEA＝∠EAB,∴五边形ABCDE是正五边形;(2)①假命题;②假命题;【知识点】三角形全等,等边对等角,正多边形