2023年中考数学 章节专项练习27 三角形（含多边形及其内角和）

这是一份2023年中考数学 章节专项练习27 三角形（含多边形及其内角和），共3页。
一、选择题
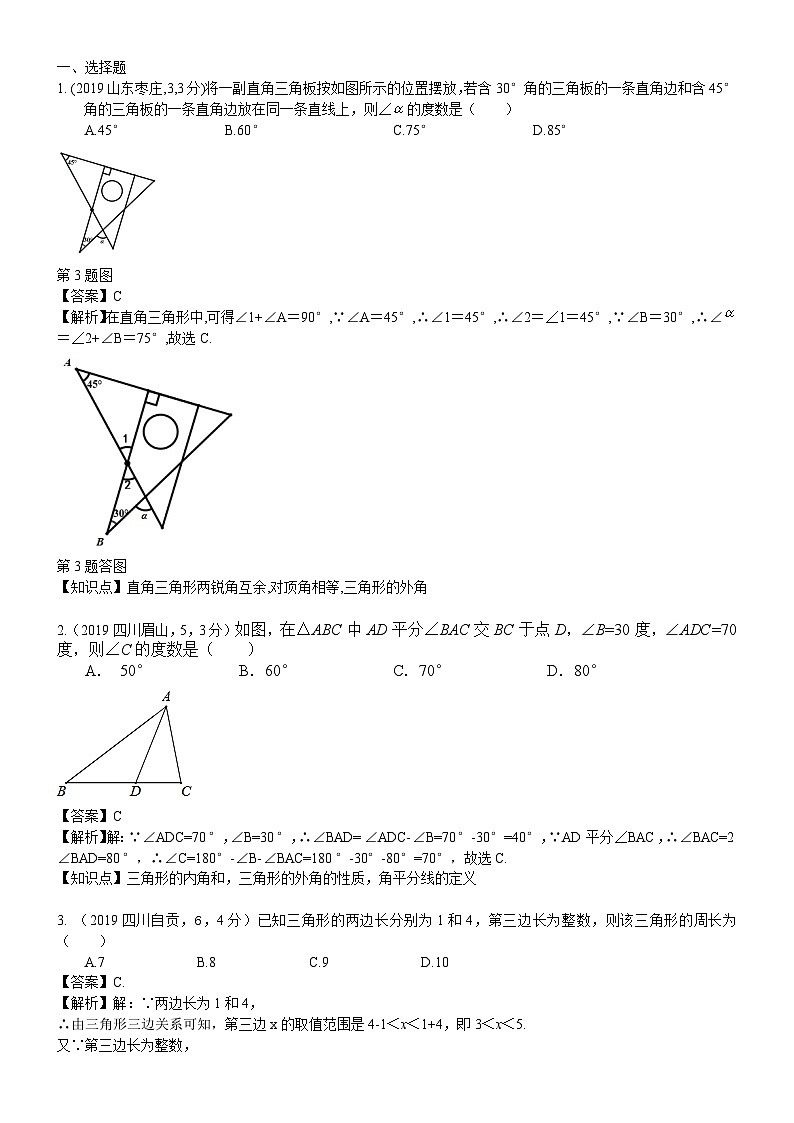
1. (2019山东枣庄,3,3分)将一副直角三角板按如图所示的位置摆放，若含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上，则∠的度数是（ ）
A.45° B.60° C.75° D.85°

第3题图
【答案】C
【解析】在直角三角形中,可得∠1+∠A＝90°,∵∠A＝45°,∴∠1＝45°,∴∠2＝∠1＝45°,∵∠B＝30°,∴∠＝∠2+∠B＝75°,故选C.

第3题答图
【知识点】直角三角形两锐角互余,对顶角相等,三角形的外角

2.（2019四川眉山，5，3分）如图，在△ABC中AD平分∠BAC交BC于点D，∠B=30度，∠ADC=70度，则∠C的度数是（ ）
A． 50° B．60° C．70° D．80°

【答案】C
【解析】解：∵∠ADC=70°，∠B=30°，∴∠BAD=∠ADC-∠B=70°-30°=40°，∵AD平分∠BAC，∴∠BAC=2∠BAD=80°，∴∠C=180°-∠B-∠BAC=180°-30°-80°=70°，故选C.
【知识点】三角形的内角和，三角形的外角的性质，角平分线的定义

3. （2019四川自贡，6，4分）已知三角形的两边长分别为1和4，第三边长为整数，则该三角形的周长为（ ）
A.7 B.8 C.9 D.10
【答案】C.
【解析】解：∵两边长为1和4，
∴由三角形三边关系可知，第三边x的取值范围是4-1＜x＜1+4，即3＜x＜5.
又∵第三边长为整数，
∴x=4.
∴该三角形周长为1+4+4=9.
故选C.
【知识点】三角形的三边关系

4.（2019浙江金华，3，3分）若长度分别为，3，5的三条线段能组成一个三角形,则a的值可以是（ ）
A.1 B. 2 C.3 D. 8
【答案】C．
【解析】根据三角形的三边关系，得2＜a＜8，故选C．
【知识点】三角形的三边关系

5. (2019浙江台州,4,4分)下列长度的三条线段,能组成三角形的是( )
A.3,4,8 B.5,6,10 C.5,5,11 D.5,6,11
【答案】B
【解析】组成三角形的三边符合任意两边之和大于第三边,任意两边之差小于第三边,只有B符合.
【知识点】三角形三边关系

6.（2019甘肃武威，6，3分）如图，足球图片正中的黑色正五边形的内角和是　　

A． B． C． D．
【答案】C
【解析】根据多边形内角和公式，得黑色正五边形的内角和为：，故选C．
【知识点】多边形内角和与外角和

7.（2019贵州黔东南，7，4分）在下列长度的三条线段中，不能组成三角形的是（　　）
A．2cm，3cm，4cm B．3cm，6cm，76cm
C．2cm，2cm，6cm D．5cm，6cm，7cm
【答案】C
【解析】解：A、2+3＞4，能组成三角形；
B、3+6＞7，能组成三角形；
C、2+2＜6，不能组成三角形；
D、5+6＞7，能够组成三角形．
故选：C．
【知识点】三角形三边关系
二、填空题
1.（2019湖南岳阳，12，4分）若一个多边形的内角和等于它的外角和，则这个多边形的边数为 .
【答案】4
【解析】设这个多边形的边数为n，根据题意得：(n－2)·180º=360º，解得：n=4．所以这个多边形的边数为4．
【知识点】多边形的内角和与外角和

2.（2019山东省济宁市，12，3分）如图，该硬币边缘镌刻的正九边形每个内角的度数是 ．

【答案】140°
【解析】法1：设正九边形的每个内角为x°，根据多边形内角和公式： (9－2)·180＝9x，解得x＝140．法2：根据多边形的外角和为360°，可知它每个外角为40°，所以内角是140°．
【知识点】多边形的内角和

3. (2019山东枣庄,16,4分)用一条宽度相等的足够长的纸条打一个结(如图1所示),然后轻轻拉紧,压平就可以得到如图2所示的正五边形ABCDE.图中,∠BAC＝________.

【答案】36°
【解析】正五边形的内角和为(5－2)×180°＝540°,∴∠ABC＝540°÷5＝108°,∵BA＝BC,∴∠BAC＝∠BCA＝36°
【知识点】正多边形,等边对等角

4.（2019广东省，13，4分）一个多边形的内角和是1080°，这个多边形的边数是　　．
【答案】8
【解析】解：设多边形边数有x条，由题意得：180（x﹣2）＝1080，解得：x＝8，
故答案为：8．
【知识点】多边形内角与外角