
2023年中考数学 章节专项练习35 与圆的有关计算
展开一、选择题
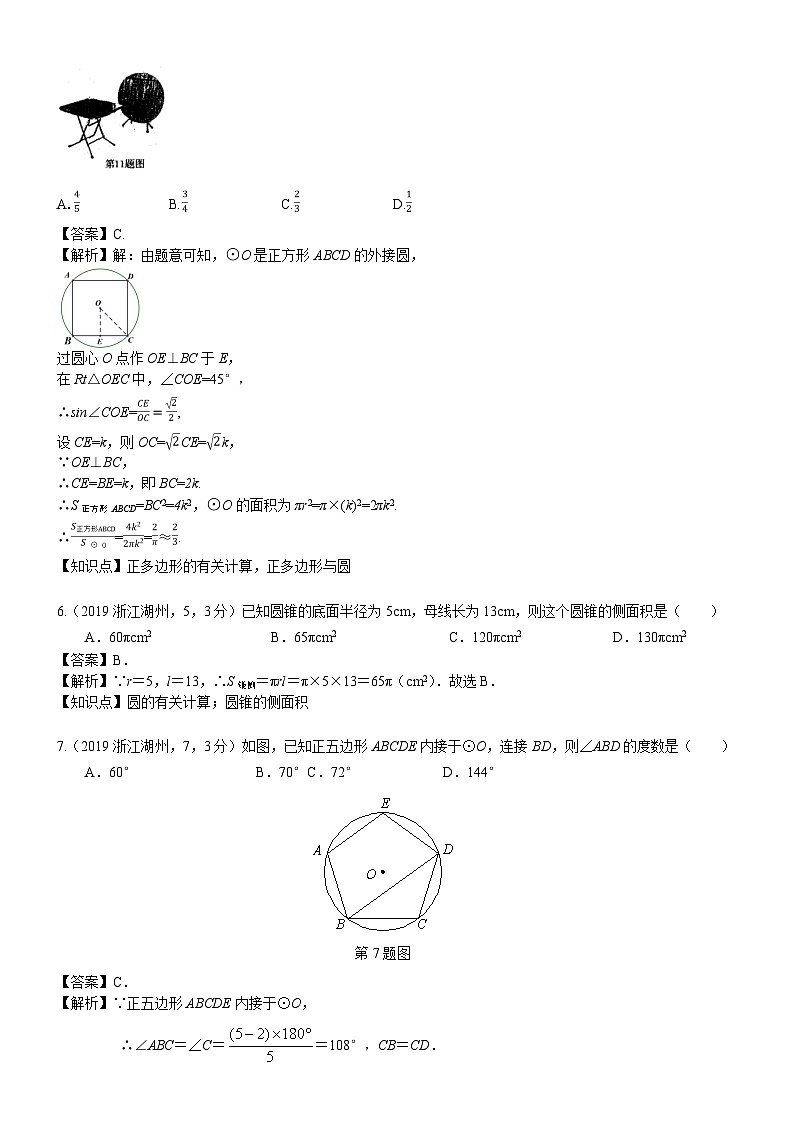
1. (2019山东泰安,11,4分)如图,将O沿弦AB折叠,恰好经过圆心O,若O的半径为3,则的长为( )
A. B. C.2 D.3
第11题图
【答案】C
【解析】连接OA,OB,过点O作OD⊥AB交于点E,由题可知OD=DE=OE=OA,在Rt△AOD中,sinA==,∴∠A=30°,∴∠AOD=60°,∠AOB=120°,==,故选C.
第11题答图
【知识点】折叠,三角函数,弧长公式
2. (2019山东枣庄,8,3分)如图,在边长为4的正方形ABCD中,以点B为圆心,AB为半径画弧,交对角线BD与点E,则图中阴影部分的面积是( )(结果保留)
A.8- B.16-2 C.8-2 D.8-
第8题图
【答案】C
【解析】在边长为4的正方形ABCD中,BD是对角线,∴AD=AB=4,∠BAD=90°,∠ABE=45°,∴S△ABD==8,S扇形ABE==8-2,故选C.
【知识点】扇形的面积,不规则图形的面积
3. (2019四川巴中,9,4分)如图,圆锥的底面半径r=6,高h=8,则圆锥的侧面积是( )
A.15 B.30 C.45 D.60
第9题图
【答案】D
【解析】圆锥的高,母线和底面半径构成直角三角形,其中r=6,h=8,所以母线为10,即为侧面扇形的半径,底面周长为12,即为侧面扇形的弧长,所以圆锥的侧面积=×10×12=60,故选D.
【知识点】勾股定理,圆周长公式,扇形面积公式
4.(2019四川凉山,11,4分)如图,在△AOC中,OA=3cm,OC=lcm,将△AOC绕点D顺时针旋转90 °后得到△BOD,则AC边在旋转过程中所扫过的图形的面积为( )cm2
A. B.2π C. D.
第11题图
【答案】B
【思路分析】先用三角形与扇形的面积和差表示AC边在旋转过程中所扫过的图形的面积,再借助全等转化为扇环的面积,最后求出扇环的面积.
【解析】AC边在旋转过程中所扫过的图形的面积=S△OCA+S扇形OAB- S扇形OCD- S△ODB①,由旋转知:△OCA≌△ODB,∴S△OCA=S△ODB,∴①式=S扇形OAB- S扇形OCD=-=2π,故选B.
第11题答图
【知识点】旋转性质;扇形面积
5.(2019四川自贡,11,4分)图中有两张型号完全一样的折叠式饭桌,将正方形桌面边上的四个弓形面板翻折起来后,就能形成一个圆形桌面(可近似看作正方形的外接圆),正方形桌面与翻折成的圆形桌面的面积之比最接近( )
A. B. C. D.
【答案】C.
【解析】解:由题意可知,⊙O是正方形ABCD的外接圆,
过圆心O点作OE⊥BC于E,
在Rt△OEC中,∠COE=45°,
∴sin∠COE=,
设CE=k,则OC=CE=k,
∵OE⊥BC,
∴CE=BE=k,即BC=2k.
∴S正方形ABCD=BC2=4k2,⊙O的面积为πr2=π×(k)2=2πk2.
∴==≈.
【知识点】正多边形的有关计算,正多边形与圆
6.(2019浙江湖州,5,3分)已知圆锥的底面半径为5cm,母线长为13cm,则这个圆锥的侧面积是( )
A.60πcm2 B.65πcm2 C.120πcm2 D.130πcm2
【答案】B.
【解析】∵r=5,l=13,∴S锥侧=πrl=π×5×13=65π(cm2).故选B.
【知识点】圆的有关计算;圆锥的侧面积
7.(2019浙江湖州,7,3分)如图,已知正五边形ABCDE内接于⊙O,连接BD,则∠ABD的度数是( )
A.60° B.70°C.72° D.144°
第7题图
【答案】C.
【解析】∵正五边形ABCDE内接于⊙O,
∴∠ABC=∠C==108°,CB=CD.
∴∠CBD=∠CDB==36°.
∴∠ABD=∠ABC-∠DBC=108°-72°=36°.
故选C.
【知识点】圆的内接正多边形有关计算;等腰三角形的性质;三角形内角和
8.(2019浙江金华,9,3分)如图,物体由两个圆锥组成,其主视图中,∠A=90°,∠ABC=105°,若上面圆锥的侧面积为1,则下面圆锥的侧面积为( )
A.2 B. C. D.
(第9题图)
【答案】D.
【解析】∵∠A=90°,∠ABC=105°,∴∠ABD=45°,∠CBD =60°,∴△ABD是等腰直角三角形,△CBD是等边三角形.设AB长为R,则BD长为R.∵上面圆锥的侧面积为1,即1=lR,∴l=·∴下面圆锥的侧面积为lR=··R=.故选D.
【知识点】圆锥的侧面积
9.(2019浙江宁波,10,4分)如图所示,矩形纸片ABCD中,AD=6cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的底面和侧面,则AB的长为( )
A.3.5cm B.4cm C.4.5cm D.5cm
第10题图
【答案】B
【解析】=,右侧圆的周长为,∵恰好能作为一个圆锥的底面和侧面,∴,=,AB=2DE,即AE=2ED,∵AE+ED=AD=6,∴AB=4,故选B.
【知识点】弧长,圆锥展开图
10.(2019浙江衢州,9,3分)如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为2的正六边形。则原来的纸带宽为( )
A.1 B. C. D.2
【答案】C
【解析】正多边形的相关计算,作AM⊥FC于M,由正六边形的性质得∠AFC=60°,因为sin∠AFM=,所以AM=sin∠AFM×AF=×2=,AM的长即为纸带宽,故选C。
【知识点】正六边形性质三角函数
二、填空题
1.(2019江苏无锡,15,2分)已知圆锥的母线成为5cm,侧面积为15π,则这个圆锥的底面圆半径为cm.
【答案】3
【解析】本题考查了圆锥的计算,∵圆锥的母线长是5cm,侧面积是15πcm2,∴圆锥的侧面展开扇形的弧长为:l6π,∵锥的侧面展开扇形的弧长等于圆锥的底面周长,∴r3cm,故答案为3.
【知识点】圆锥计算
2.(2019山东滨州,17,5分)若正六边形的内切圆半径为2,则其外接圆半径为____________.
【答案】
【思路分析】根据题意画出图形,作一条内切圆半径和一条外接圆半径,在组成的直角三角形中,利用勾股定理或锐角三角函数求值.
【解题过程】如图,连接OE,作OM⊥EF于M,则OE=EF,EM=FM,OM=2,∠EOM=30°,在Rt△OEM中,cos∠EOM=,∴=,解得OE=,即外接圆半径为.
【知识点】正六边形的性质;勾股定理;锐角三角函数
3. (2019山东聊城,14,3分)如图是一个圆锥的主视图,根据图中标出的数据(单位:cm),计算这个圆锥侧面展开图圆心角的度数为________.
第14题图
【答案】120°
【解析】由图可知,圆锥的底面周长为2,圆锥的母线AC=3,∴设圆锥侧面展开图圆心角的度数为n°,根据弧长公式可得2=,n=120.∴圆心角的度数为120.
【知识点】勾股定理,弧长公式
4. (2019山东泰安,15,4分)如图,∠AOB=90°,∠B=30°,以点O为圆心,OA为半径作弧交AB于点A,点C,交OB于点D,若OA=3,则阴影部分的面积为________.
第15题图
【答案】
【解析】连接OC,过点C作CN⊥AO于点N,CM⊥OB于点M,∠AOB=90°,∠B=30°,∴∠A=60°,∵OA=OC,∴△AOC为等边三角形,∵OA=3,∴CN=,CM=CN=,∴S扇形AOC=,S△AOC=,在Rt△AOB中,OB=OA=3,S△OCB=,∠COD=30°,S扇形COD=,S阴影=S扇形AOC-S△AOC+S△OCB-S扇形COD=.
第15题答图
【知识点】扇形面积,三角形面积
5.(2019山东潍坊,18,3分)如图所示,在平面直角坐标系xoy中,一组同心圆的圆心为坐标原点O,它们的半径分别为1,2,3,…,按照“加1”依次递增;一组平行线l0,l1,l2,l3,…都与x轴垂直,相邻两直线的间距为1,其中l0与y轴重合.若半径为2的圆与l1在第一象限内交于点P1,半径为3的圆与l2在第一象限内相交于点P2,…,半径为n+1的圆与ln在第一象限内交于点Pn,则点Pn的坐标为 .(n为正整数)
【答案】(n,)
【思路分析】横坐标依次为1,2,3,4,…可以确定点Pn的横坐标,再根据勾股定理可确定点Pn的纵坐标.
【解题过程】由图可知点Pn的横坐标与它所在圆的半径相同,故点Pn的横坐标为n,
点P1的纵坐标为,
点P2的纵坐标为,
……
点Pn的纵坐标为,
∴点Pn的坐标为(n,).
【知识点】规律探索,图形与坐标
6.(2019重庆市B卷,16,4分)如图,四边形ABCD是矩形,AB=4,AD=2,以点A为圆心,AB长为半径画弧,交CD于点E,交AD的延长线于点F,则图中阴影部分的面积是
【答案】8-8
【解题过程】连结AE.
∵在矩形ABCD中,AB=4,AD=2,∴AB=AD,∴∠EAD=∠EAB=45°,∴AE=AD=2,
∴ = =×(8-2)×2-×2×2=8-8
【知识点】扇形面积的计算
7.(2019重庆A卷,16,4)如图,在菱形ABCD中,对角线AC,BD交于点O,∠ABC=60°,AB=2,分别以点A、点C为圆心,以AO的长为半径画弧分别与菱形的边相交,则图中阴影部分的面积为 .(结果保留)
第16题图
【答案】.
【解析】∵在菱形ABCD中,∠ABC=60°,∴△ABC是正三角形,且∠BAD=∠BCD=120°.∴S阴影=2S正三角形ABC-2S阴影AEF=2××22-2×=.如下图:
第16题答图
【知识点】菱形;等边三角形的面积;扇形的面积.
8.(2019甘肃天水,16,4分)如图,在平面直角坐标系中,已知⊙D经过原点O,与x轴、y轴分别交于A、B两点,点B坐标为(0,2),OC与⊙D交于点C,∠OCA=30°,则圆中阴影部分的面积为 .
【答案】2π﹣2
【解析】解:连接AB,
∵∠AOB=90°,
∴AB是直径,
根据同弧对的圆周角相等得∠OBA=∠C=30°,
∵OB=2,
∴OA=OBtan∠ABO=OBtan30°=22,AB=AO÷sin30°=4,即圆的半径为2,
∴S阴影=S半圆﹣S△ABO2×22π﹣2.
故答案为:2π﹣2.
【知识点】坐标与图形性质;圆周角定理;扇形面积的计算
9.(2019甘肃武威,16,4分)把半径为1的圆分割成四段相等的弧,再将这四段弧依次相连拼成如图所示的恒星图形,那么这个恒星图形的面积等于 .
【答案】.
【解析】解:如图:
新的正方形的边长为,∴恒星的面积.
故答案为.
【知识点】扇形面积
10.(2019甘肃省,16,3分)如图,在中,,,点是的中点,以、为圆心,、长为半径画弧,分别交、于点、,则图中阴影部分的面积为 .
【答案】
【解析】解:在中,,,
,,
是的中点,
,
,
故答案为:
【知识点】扇形面积
11.(2019广东广州,15,3分)如图放置的一个圆锥,它的主视图是直角边长为2的等腰直角三角形,则该圆锥侧面展开扇形的弧长为 .(结果保留π)
【答案】
【解析】解:∵某圆锥的主视图是一个腰长为2的等腰直角三角形,
∴斜边长为2,则底面圆的周长为2π,
∴该圆锥侧面展开扇形的弧长为2π,
故答案为2π.
【知识点】等腰直角三角形;弧长的计算;圆锥的计算
12.(2019湖北鄂州,13,3分)一个圆锥的底面半径r=5,高h=10,则这个圆锥的侧面积是 .
【答案】
【解析】解:∵圆锥的底面半径r=5,高h=10,
∴圆锥的母线长为5,
∴圆锥的侧面积为π×55,
故答案为:.
【知识点】圆锥的计算
三、解答题
1.(2019浙江衢州,21,8分)如图,在等腰△ABC中,AB=AC.以AC为直径作⊙O交BC于点D,过点D作DE⊥AB,垂足为E.
(1)求证:DE是⊙O的切线。
(2)若DE=,∠C=30°,求的长。
【思路分析】(1)连结OD,根据等腰三角形的性质及垂直的定义证明∠ODE=90°;
(2)根据等腰三角形的性质得到∠B=30°,∠AOD=60°,利用三角函数求得BD,CD,OC,利用弧长公式求得的长。
【解题过程】(1)证明:如图,连结OD,∵OC=0D.AB-AC,
∴∠1=∠C.∠C=∠B.……1分
∴∠1=∠B.…2分
∵DE⊥AB,
∴∠2+∠B=90°.
∴∠2+∠1=90°,…3分
∴∠ODE=90°,…4分
∴DE为⊙O的切线。
(2)连结AD,∵AC为⊙O的直径,
∴∠ADC=90°. …5分
∵AB=AC,
∴∠B=∠C=30°,BD=CD.
∴∠AOD=60°. …6分
∵DE=,
∴BD=CD=2,
∴0C=2 …7分
∴==π。…8分
【知识点】切线判定三角函数弧长计算等腰三角形的性质
2.(2019四川巴中,19,8分)△ABC在边长为1的正方形网格中如图所示.
①以点C为位似中心,作出△ABC的位似图形△A1B1C,使其位似比为1:2,且△A1B1C位于点C的异侧,并表示出A1的坐标;
②作出△ABC绕点C顺时针旋转90°后的图形△A2B2C;
③在②的条件下,求出点B经过的路径长.
第19题图
【思路分析】①以点C为位似中心,延长AC,BC至A1,B1,使A1C=2AC,B1C=2BC;②过点C作AC,BC的垂线,截取A2C=AC,B2C=BC,连接A2B2;③点B的路径为圆弧,半径为BC的长,圆心角为90°,根据弧长公式可求.
【解题过程】①如图所示即为所求的△A1B1C,点A1的坐标为(3,-3);②如图所示即为所求的△A2B2C;③点B绕点C顺时针旋转90°,半径为BC=,所以路径长为=.
第19题图
【知识点】位似图形,旋转,弧长公式
3.(2019四川巴中,25,10分)如图,在菱形ABCD中,连接BD,AC交于点O,过点O作OH⊥BC于点H,以点O为圆心,OH为半径的半圆交AC于点M.
①求证:DC是O的切线;
②若AC=4MC且AC=8,求图中阴影部分的面积;
③在②的条件下,P是线段BD上的一动点,当PD为何值时,PH+PM的值最小,并求出最小值.
第25题图
【思路分析】①过点O作CD的垂线,通过证明其与半径相等,得到CD是切线;②通过三角函数计算边长和圆心角度数,得到三角形和扇形的面积,可得阴影部分面积③根据轴对称的性质找到点P的位置,进而计算最小值,利用三角函数求PD的长度.
【解题过程】①过点O作OG⊥CD于点G,菱形ABCD中,AC是对角线,所以AC平分∠BCD,因为OH⊥BC,所以OH=OG,因为OH是O的半径,所以OG等于O的半径,所以CD是O的切线;
第25题答图(1)
②因为AC=4MC且AC=8,所以OC=2MC=4,MC=OM=2,∴OH=OM=2,在Rt△OHC中,OH=2,OC=4,所以HC==,tan∠HOC=,∴∠HOC=60°,所以S阴影=S△OCH-S扇形OHM==-;
③作点M关于BD的对称点N,连接HN交BD于点P,此时PH+PM的值最小.因为ON=OM=OH,∠MOH=60°,所以∠MNH=30°,∠MNH=∠HCM,所以HN=HC=,即PH+PM的最小值为.在Rt△NPO中,OP=ONtan30°=,在Rt△COD中,OD=OCtan30°=,所以PD=OP+OD=.
第25题答图(2)
【知识点】菱形性质,角平分线性质,切线判定,勾股定理,三角函数,扇形面积,轴对称性质
4.(2019山东淄博,22,8分)如图,在Rt△ABC中,∠B=90°,交BC于点D,点E在AC上,以AE为直径的⊙O经过点D.
(1)求证:①BC是⊙O的切线;
②CD2=CE×CA;
(2)若点F是劣弧AD的中点,且CE=3,试求阴影部分的面积。
【思路分析】(1)①BC是⊙O的切线,需连接DO,再证DO⊥BC;
②由CD2=CE×CA,需证=,从而证△CDE∽△CAD;
(2)由F为弧AD的中点可得△DFO、△AOF是等边三角形,由此求出⊙O的半径.
【解题过程】(1)①连接DO,∵AD平分∠BAC,∴∠BAD=∠EAD,∵DO=AO,∴∠EAD=∠ADO,∴∠BAD=∠ADO,∴BA∥DO,∴∠CDO=∠B,∵∠B=90°,∴∠CDO=90°,∴BC是⊙O的切线;
②连DE,∵AE是直径,∴∠ADE=90°,∴∠CDE+∠ADB=90°,又∵∠ADB+∠BAD=90°,∠BAD=∠DAE,∴∠CDE=∠DAE,又∵∠C=∠C,∴△CDE∽△CAD,∴=,∴CD2=CE×CA;
(2)连接OD、FO、DF,∵点F是劣弧AD的中点,∴=,∴∠AOF=∠DOF,∠BAD=∠ADF,∵∠BAD=∠EAD,∴∠EAD=∠ADF,∴DF∥AC,∴∠AOF=∠DFO,又∵∠DFO=∠FDO,∴∠DFO=∠FDO=∠DOF=60°,又∴DF∥AC,∴S△DFA=S△DFO,
连DE,∴△DEO是等边三角形,∴∠CDE=30°=∠C,∴CE=DE=DO=3,
∴S阴影=S扇形DFO=×π×32=π.
【知识点】切线判定方法,相似三角形的判定,等边三角形判定,等底等高的三角形面积相等,扇形面积计算.
5.(2019山东滨州,25,13分)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F.
(1)求证:直线DF是⊙O的切线;
(2)求证:BC2=4CF•AC;
(3)若⊙O的半径为4,∠CDF=15°,求阴影部分的面积.
【思路分析】(1)如图所示,连接OD,证明∠CDF+∠ODB=90°,即可求解;(2)证明△CFD∽△CDA,则CD2=CF•AC,即BC2=4CF•AC;(3)S阴影部分=S扇形OAE-S△OAE即可求解.
【解题过程】
解:(1)如图所示,连接OD,
∵AB=AC,∴∠ABC=∠C,而OB=OD,∴∠ODB=∠ABC=∠C,
∵DF⊥AC,∴∠CDF+∠C=90°,∴∠CDF+∠ODB=90°,
∴∠ODF=90°,
∴直线DF是⊙O的切线.………………………………………………………………………4分
(2)连接AD,则AD⊥BC,则AB=AC,
则DB=DC=.………………………………………………………………………………6分
∵∠CDF+∠C=90°,∠C+∠DAC=90°,∴∠CDF=∠DCA,
而∠DFC=∠ADC=90°,∴△CFD∽△CDA,
∴CD2=CF•AC,即BC2=4CF•AC.…………………………………………………………8分
(3)连接OE,
∵∠CDF=15°,∠C=75°,∴∠OAE=30°=∠OEA,
∴∠AOE=120°,
S△OAE=AE×OEsin∠OEA=×2×OE×cos∠OEA×OEsin∠OEA=4,…………12分
S阴影部分=S扇形OAE-S△OAE=×π×42-4=-4.………………………13分
【知识点】圆周角定理及推论;切线的判定;相似三角形的判定与性质;锐角三角函数
6.(2019江苏省无锡市,24,8)一次函数的图像与x轴的负半轴相交于点A,与y轴的正半轴相交于点B,且△OAB的外接圆的圆心M的横坐标为-3.
(1)求一次函数的解析式;
(2)求图中阴影部分的面积.
第24题图
【思路分析】
本题考查一次函数与圆的综合题.(1)作MN⊥BO,先用由垂径定理求 OA得A的坐标,再利用解直角三角形求OB以及B的坐标,最求用待定系数法求一次函数的解析式;
(2)转化为扇形面积与三角形面积的差即可.
【解题过程】
解:(1)作MN⊥BO,由垂径定理得N为OB中点,MN=OA,∵MN=3,∴OA=6,即A(-6,0).
∵sin∠ABO=,OA=6,∴OB= 2,B(0, 2),设y = kx +b,将A、B坐标代入得,解得,∴y = x +2;
(2)∵第一问解得∠ABO=60°,∴∠AMO=120°,
所以阴影部分面积为S=.
第24题答图
【知识点】一次函数;垂径定理;扇形面积
7.(2019广东省,22,7分)在如图所示的网格中,每个小正方形的边长为1,每个小正方形的顶点叫格点,△ABC的三个顶点均在格点上,以点A为圆心的与BC相切于点D,分别交AB、AC于点E、F.
(1)求△ABC三边的长;
(2)求图中由线段EB、BC、CF及所围成的阴影部分的面积.
【思路分析】(1)根据勾股定理即可求得;
(2)根据勾股定理求得AD,由(1)得,AB2+AC2=BC2,则∠BAC=90°,根据S阴=S△ABC﹣S扇形AEF即可求得.
【解题过程】解:(1)AB2,
AC2,
BC4;
(2)由(1)得,AB2+AC2=BC2,
∴∠BAC=90°,
连接AD,AD2,
∴S阴=S△ABC﹣S扇形AEFAB•ACπ•AD2=20﹣5π.
【知识点】勾股定理;切线的性质;扇形面积的计算
人教版九年级数学上册 24.49 《圆》-正多边形与圆及有关圆的计算(专项练习): 这是一份人教版九年级数学上册 24.49 《圆》-正多边形与圆及有关圆的计算(专项练习),共34页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
备战2023年中考数学基础题型专项突破练习(全国通用)冲刺小卷24 与圆有关的计算: 这是一份备战2023年中考数学基础题型专项突破练习(全国通用)冲刺小卷24 与圆有关的计算,文件包含冲刺小卷24与圆有关的计算-老师版docx、冲刺小卷24与圆有关的计算-学生版docx等2份试卷配套教学资源,其中试卷共10页, 欢迎下载使用。
2023届中考数学高频考点专项练习:专题十五 考点35 与圆有关的计算(B): 这是一份2023届中考数学高频考点专项练习:专题十五 考点35 与圆有关的计算(B),共13页。












