安徽省合肥市六校2022-2023学年高一下学期期末联考数学试卷（含答案）

这是一份安徽省合肥市六校2022-2023学年高一下学期期末联考数学试卷（含答案），共17页。试卷主要包含了选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

安徽省合肥市六校2022-2023学年高一下学期期末联考数学试卷
学校：___________姓名：___________班级：___________考号：___________

一、选择题
1、若复数z满足，则( )
A.1 B.5 C.7 D.25
2、的值为( )
A. B. C. D.
3、从装有2个红球和2个黑球的口袋内任取2个球，那么互斥而不对立的两个事件是( )
A.至少有一个黑球与都是黑球 B.至少有一个黑球与都是红球
C.恰有一个黑球与恰有两个黑球 D.至少有一个黑球与至少有一个红球
4、已知命题，命题，若是的充分不必要条件，则实数m的取值范围是( )
A. B.
C. D.
5、已知表示不超过实数x的最大整数，为取整函数，是函数的零点，则( )
A.4 B.5 C.2 D.3
6、设m，n是两条不同的直线，，是两个不同的平面，下列命题中正确的是
A.若，，，则
B.若，，，则
C.若，，，则
D若，，，则
7、一个电路如图所示，A，B，C，D，E，F为6个开关，其闭合的概率为，且是相互独立的，则灯亮的概率是( )

A. B. C. D.
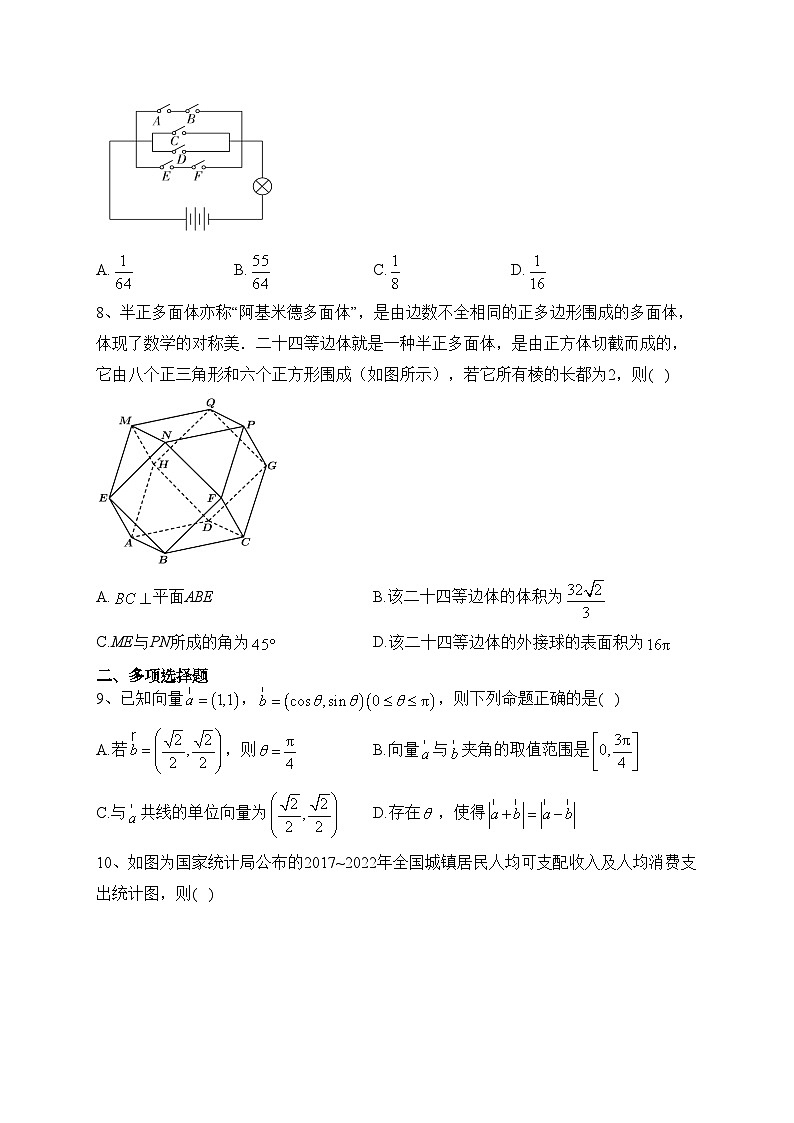
8、半正多面体亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美．二十四等边体就是一种半正多面体，是由正方体切截而成的，它由八个正三角形和六个正方形围成（如图所示），若它所有棱的长都为2，则( )

A.平面ABE B.该二十四等边体的体积为
C.ME与PN所成的角为 D.该二十四等边体的外接球的表面积为
二、多项选择题
9、已知向量，，则下列命题正确的是( )
A.若，则 B.向量与夹角的取值范围是
C.与共线的单位向量为 D.存在，使得
10、如图为国家统计局公布的2017~2022年全国城镇居民人均可支配收入及人均消费支出统计图，则( )

A.2017~2022年全国城镇居民人均可支配收入及人均消费支出均呈增长趋势
B.2017~2022年全国城镇居民人均消费支出的中位数为27535
C.2017~2022年全国城镇居民人均可支配收入的极差大于人均消费支出的极差
D.2017~2022年全国城镇居民人均消费支出占人均可支配收入的比例均大于80%
11、关于函数f(x)＝sin|x|＋|sin x|的叙述正确的是( )
A.是偶函数` B.在区间单调递增
C.在有4个零点 D.的最大值为2
12、已知正方体，则( )
A.直线与所成的角为 B.直线与所成的角为
C.直线平面所成的角为 D.直线与平面所成的角为
三、填空题
13、函数的最小值为______．
14、已知非零向量，满足，且，则与的夹角为__________.
15、在中，若，则的形状为_________.
16、从2至8的7个整数中随机取2个不同的数，则这2个数互质的概率为___________.
四、解答题
17、已知一个圆锥的底面半径为R，高为h，在其内部有一个高为x的内接圆柱．
（1）求圆柱的侧面积；
（2）求圆柱的侧面积的最大值及此时的值．
18、已知向量，，.
（1）求的值；
（2）若，，且，求的值.
19、定义在上的奇函数，已知当时，．
（1）求在上的解析式；
（2）若使不等式成立，求实数m的取值范围．
20、在中，内角A,B,C的对边分别为a,b,c，设的面积为S，满足.
（1）求角C；
（2）若，求周长最大值.
21、随着老年人消费需求从“生存型”向“发展型”转变．消费层次不断提升，“银发经济”成为社会热门话题之一，被各企业持续关注.某企业为了解该地老年人消费能力情况，对该地年龄在的老年人的年收入按年龄，分成两组进行分层抽样调查，已知抽取了年龄在的老年人500人．年龄在的老年人300人．现作出年龄在的老年人年收入的频率分布直方图（如下图所示）．

（1）根据频率分布直方图，估计该地年龄在的老年人年收入的平均数及第95百分位数；
（2）已知年龄在的老年人年收入的方差为3，年龄在的老年人年收入的平均数和方差分别为3.75和1.4，试估计年龄在的老年人年收入的方差．
22、如图，AB是半球的直径，O为球心，,M,N依次是半圆上的两个三等分点，P是半球面上一点，且.

（1）证明：平面平面PON；
（2）若点P在底面圆内的射影恰在BM上，求二面角的余弦值．
参考答案
1、答案：B
解析：由题意有，故．
故选：B．
2、答案：A
解析：


.
故选：A.
3、答案：C
解析：依题意，记2个红球为a,b，2个黑球为m,n，
则从中任取2个球的总的基本事件为ab,am,an,bm,bn,mn，
对于A，至少有一个黑球的基本事件为am,an,bm,bn,mn，都是黑球的基本事件为mn，
显然两个事件有交事件mn，所以不为互斥事件，故A错误；
对于B，至少有一个黑球的基本事件为am,an,bm,bn,mn，都是红球的基本事件为ab，
显然两个事件不仅是互斥事件，也是对立事件，故B错误；
对于C，恰有一个黑球的基本事件为am,an,bm,bn，恰有两个黑球的基本事件为mn，
显然两个事件是互斥事件，但不是对立事件，故C正确；
对于D，至少有一个黑球的基本事件为am,an,bm,bn,mn，至少有一个红球的基本事件为ab,am,an,bm,bn，
显然两个事件不是互斥事件，故D错误.
故选：C.
4、答案：B
解析：由得或,因为是的充分不必要条件,所以q是p的充分不必要条件,所以,解得或.
故选:B.
5、答案：C
解析：函数在递增，
且，，
所以函数存在唯一的零点，
故，
故选：C.
6、答案：D
解析：，,,,,故选D.
7、答案：B
解析：设A与B中至少有一个不闭合的事件为与至少有一个不闭合的事件为R，
则，
所以灯亮的概率为，
故选B.
8、答案：D
解析：依题意，补齐正方体，如下图，

对于A，假设平面ABE，平面ABE，
，，
二十四等边体就是一种半正多面体，
由对称性可知，六边形EBCGQM为正六边形，
，
这与“”矛盾，所以假设不成立，A错误；
对于B，，正方体的棱长为，
该二十四等边体的体积为正方体体积去掉个三棱锥体积，
即，B错误；
对于C，，
为异面直线ME与PN所成角（或补角），
在等边中，，C错误；
对于D，如图，取正方形ACPM对角线交点为O，
即为该二十四等边体的外接球球心，

在等腰中，，
在正方形ACPM中，，
即外接球半径，
该二十四等边体的外接球的表面积，D正确.
故选：D.
9、答案：ABD
解析：对于A，若，则，即，
又，则，故A正确；
对于B，设向量与的夹角为，
则，
因为，则，所以，即，
又，所以，即向量与夹角的取值范围是，故B正确；
对于C，与共线的单位向量为或，即或，故C错误；
对于D，假设存在，使得，
则，即，则，
所以，即，又，则，故D正确.
故选：ABD.
10、答案：BC
解析：对于选项A：由图知2017~2022年全国城镇居民人均可支配收入呈增长趋势，但人均消费支出2020年比2019年少，故A不正确；
对于选项B：由图可知2017~2022年全国城镇居民人均消费支出的中位数为，故B正确；
对于选项C：2017~2022年全国城镇居民人均可支配收入的极差为，
人均消费支出的极差为，
因为，所以人均可支配收入的极差大于人均消费支出的极差，故C正确；
对于选项D：2022年全国城镇居民人均消费支出占人均可支配收入的比例为，小于80%，故D不正确.
故选：BC.
11、答案：AD
解析：A.，是偶函数，故A正确；
B.当时，，在单调递减，故B错误；
C.当时，令，得或，又在上为偶函数，
在上的根为，0，，有3个零点，故C错误；
D.，，当或时两等号同时成立，
的最大值为2，故D正确．
故选：AD
12、答案：ABC
解析：对于A，连接，，由正方体的性质知：，
直线与所成的角即为与所成的角，
因为为等边三角形，所以直线与所成角为，故A正确；

对于B，连接，,因为平面，平面，
所以，又因，，所以，
,,平面，所以平面，
平面，所以，所以直线与所成的角为，故B正确；

对于C，因为平面，所以直线平面所成的角为，
，所以直线平面所成的角为，故C正确；

对于D，连接,交于点O，因为平面，
平面，所以，又因为，
,,平面，所以平面，
所以直线与平面所成的角为，
设正方体的边长为2，所以，
，所以，所以，
所以直线与平面所成的角为，故D错误.
故选：ABC.

13、答案：
解析：因为，
令，则，则，
因为，当且仅当时，等号成立，
所以的最小值为.
故答案为：.
14、答案：
解析：因为，故，
即，
由于，故，
因为，故，
故答案为：
15、答案：等腰或直角三角形
解析：，
由正弦定理可得，
所以，，
即，
，
或，
，或.
因此，为等腰或直角三角形.
故答案为：等腰或直角三角形.
16、答案：
解析：从2至8的整数有2,3,4,5,6,7,8，
互质的两个数有2和3,2和5,2和7,3和4,3和5,3和7,3和8,4和5,4和7,5和6,5和7,5和8,6和7,7和8，共14对，
所以随机取2个数，互质的概率为.
故答案为：.
17、答案：（1）
（2）当时，
解析：（1）设圆锥顶点为S，底面圆心为O，圆柱的底面半径为，
作出圆锥和圆柱的轴截面如下图所示，

，，则
圆柱侧面积.
（2）由（1）知：，
当时，圆柱侧面积取得最大值.
18、答案：(1)
(2)
解析：根据题意，由于向量，,那么可知
,,,
（2）根据题意，由于,且，
那么
19、答案：（1）
（2）
解析：（1）因为是定义在上的奇函数，时，，
所以，解得，
所以时，，
当时，，
所以，
又，
所以，，
即在上的解析式为.
（2）因为时，，
所以可化为，整理得，
令，
根据指数函数单调性可得，与都是减函数，
所以也是减函数，，
所以，
故实数m的取值范围是.
20、答案：（1）
（2）9
解析：（1）因为，
所以.
因为，所以，所以.
由余弦定理，得，整理，得.
由余弦定理，得，
因为，所以；
（2）因为，所以根据正弦定理，得，所以.
在中，由余弦定理，得，整理得，
因为， 所以，
整理可得即，当且仅当时等号成立，
所以取得最大值是6，当时取到,
所以周长的最大值为9.
21、答案：（1）5.35；8.3
（2）3
解析：（1）频率分布直方图中，该地年龄在的老年人年收入的平均数约为：
，
由频率分布直方图，年收入在8.5万元以下的老年人所占比例为，
年收入在7.5万元以下的老年人所占比例为，
因此，第95百分位数一定位于内，
由，
可以估计该地年龄在的老年人年收入的第95百分位数为8.3.
（2）设年龄在的老年人样本的平均数记为，方差记为；
年龄在的老年人样本的平均数记为，方差记为；
年龄在的老年人样本的平均数记为，方差记为.
由（1）得，由题意得，，，，
则，
由，
可得，
即估计该地年龄在的老年人的年收入方差为3.
22、答案：（1）证明见解析；
（2）.
解析：（1）连接OM，MN，如图，M,N是半圆上的两个三等分点，
则有，

而，即有,都为正三角形，因此，，
四边形OMNB是菱形，，而，，PN,平面PON，
因此，平面PON，平面PBM，
所以平面平面PON.
（2）由（1）知，平面平面OMNB，平面平面，
则点P在底面圆内的射影在ON上，
因点P在底面圆内的射影在BM上，因此，点P在底面圆内的射影是ON与MB的交点Q，
即平面OMNB，有，，
，而，即有，
取PB的中点C，连CN,CO，于是得，则有是二面角的平面角，
在中，，
所以，
所以二面角的余弦值是.