北师大版八年级上册第二章 实数1 认识无理数学案

这是一份北师大版八年级上册第二章 实数1 认识无理数学案，共3页。学案主要包含了学习目标，学习策略，学习过程等内容，欢迎下载使用。
第二章  实数1  认识无理数【学习目标】1．掌握无理数的概念，并能辨别出一个数是无理数还是有理数．2．掌握无理数与有理数的区别，会对无理数进行估算.对所学的数进行分类 .3. 准确认识到有理数都可以划成有限小数和无限循环小数，培养抽象概括思维意识.【学习策略】1.认识有理数与无理数的区别，能准确区分；2.准确对有理数与无理数在小数方面的分类。【学习过程】 一.复习回顾提出问题：1. 一个整数的平方一定是整数吗？2. 一个分数的平方一定是分数吗？二.新课学习：自学课本本节内容思考下列问题：1.我们以前都学过哪些数，分别举例说明？2.我们以前都学过哪些数，分别举例说明？ 3.如果a2=3，那么a是整数吗？是分数吗？为什么？4.借助计算器用无限逼近的思想，并参照课本22页表格计算：如果x2=5，你能算出x的值吗？5.什么是无理数，你有举出几种不同类型的无理数？6.你能从小数的角度上对有理数和无理数进行分类吗？三.尝试应用：1. 以下各正方形的边长是无理数的是（       ）A.面积为25的正方形；             B.面积为的正方形；C.面积为8的正方形；              D.面积为1.44的正方形. 2. 实数π，，0，﹣1中，无理数是        3. 一个直角三角形两条直角边的长分别是3和5，则斜边a是有理数吗?  四.自主总结：1.2.无理数是        小数,有理数是     小数或       小数.3.任何一个有理数都可以化成          ,而无理数则不能.4．π是         数。（填有理或无理）五.达标测试1．在下列实数中：0，，﹣3.1415，，，0.343343334…无理数有（　　）A．1个 B．2个 C．3个 D．4个2．下列各数中，是无理数的（　　）A．π B．0 C． D．﹣3．如图，在5×5的正方形网格中，以AB为边画直角△ABC，使点C在格点上，且另外两条边长均为无理数，满足这样条件的点C共       个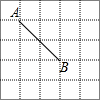．4．若无理数a满足：﹣4＜a＜﹣1，请写出两个你熟悉的无理数：　      ，       ．5．在：，，0，3.14，﹣，﹣，7.151551…（每相邻两个“1”之间依次多一个“5”）中，整数集合{　　                         　　…}，分数集合{　　                         　　…}，无理数集合{　　                         　…}．6.国涛同学家的客厅是面积为28平方米的正方形，那么请你判断一下这个正方形客厅的边长x是不是有理数？如果误差要求小于0.01米，那么边长x的最大取值是多少（精确到0.001）？  三.尝试应用答案1. C       2.π       3.解：不是，是无理数. 达标测试答案1．B  2．A3．4 解析：如图所示，满足条件的点C有4个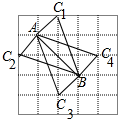．故答案为4．4． ﹣，﹣π．解析：无理数有：﹣，﹣π．（答案不唯一）．5．解：整数集合{0，﹣…}；分数集合{，3.14…}；无理数集合{，﹣，7.151551…}．6．解：=2，这个正方形客厅的边长x不是有理数，2≈2×2.6457≈5.291．