广东省梅州市大埔县广德中学2022-2023学年七年级下学期期末数学试卷（含答案）

这是一份广东省梅州市大埔县广德中学2022-2023学年七年级下学期期末数学试卷（含答案），共14页。

大埔县广德中学2022-2023学年七年级（下）期末数学试卷
一．选择题（共10小题，满分30分，每小题3分）
1．（3分）32×37的值是（　　）
A．39 B．314 C．35 D．311
2．（3分）纳米（nm）是一种长度单位，1nm为十亿分之一米．海思麒麟990处理器使用7nm工艺制造，其中7nm用科学记数法可表示为（　　）
A．7×10﹣8m B．0.7×10﹣8m C．7×10﹣9m D．0.7×10﹣9m
3．（3分）下列标志中，可以看作是轴对称图形的是（　　）
A． B．
C． D．
4．（3分）下列运算正确的是（　　）
A．a2•a3＝a6 B．（﹣3a）3＝﹣9a3
C．a6÷a2＝a3 D．（﹣a2b）3＝﹣a6b3
5．（3分）下列事件中，属于必然事件的是（　　）
A．地球绕太阳公转
B．一个月有32天
C．一位射击运动员每次射击的命中环数
D．任意买一张电影票，座位号是3的倍数
6．（3分）一辆汽车从A地启动，加速一段时间后保持匀速行驶，接近B地时开始减速，到达B地时恰好停止，如所示的哪一幅图可以近似地刻画出汽车在这段时间内的速度变化情况（　　）
A． B．
C． D．
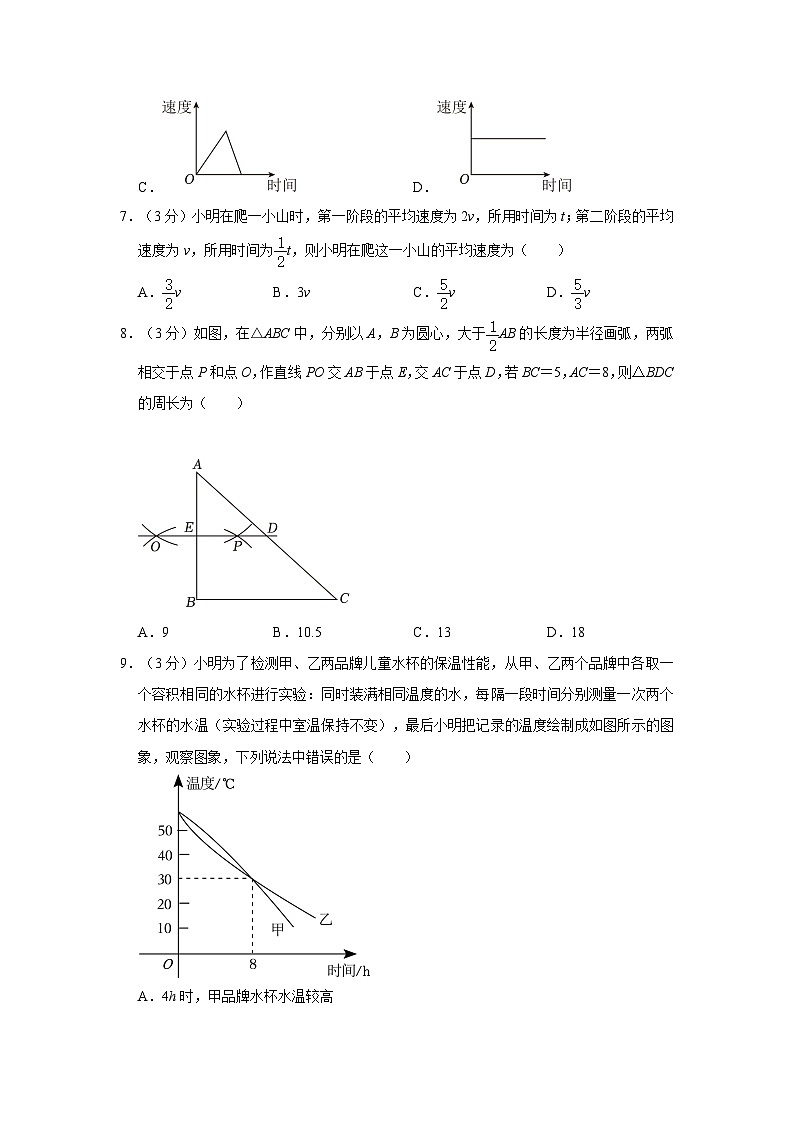
7．（3分）小明在爬一小山时，第一阶段的平均速度为2v，所用时间为t；第二阶段的平均速度为v，所用时间为t，则小明在爬这一小山的平均速度为（　　）
A．v B．3v C．v D．v
8．（3分）如图，在△ABC中，分别以A，B为圆心，大于AB的长度为半径画弧，两弧相交于点P和点O，作直线PO交AB于点E，交AC于点D，若BC＝5，AC＝8，则△BDC的周长为（　　）
​

A．9 B．10.5 C．13 D．18
9．（3分）小明为了检测甲、乙两品牌儿童水杯的保温性能，从甲、乙两个品牌中各取一个容积相同的水杯进行实验：同时装满相同温度的水，每隔一段时间分别测量一次两个水杯的水温（实验过程中室温保持不变），最后小明把记录的温度绘制成如图所示的图象，观察图象，下列说法中错误的是（　　）

A．4h时，甲品牌水杯水温较高
B．8h时，甲、乙两品牌水杯水温相同
C．甲、乙两品牌水杯水温都随着时间的增加而降低
D．8h以后，乙品牌水杯水温下降更快
10．（3分）如图，长方形ABCD中，点E为AD上一点，连接CE，将长方形ABCD沿着直线CE折叠，点D恰好落在AB的中点F上，点G为CF的中点，点P为线段CE上的动点，连接PF、PG，若AE＝a、ED＝b、AF＝c，则PF+PG的最小值是（　　）

A．a+c﹣b B．b+2c C．a+b+2c D．a+b
二．填空题（共5小题，满分15分，每小题3分）
11．（3分）（）﹣1＝　 　．
12．（3分）一个角等于30°，它的补角等于　 　°．
13．（3分）如图，在△ABC和△DEF中，点B，F，C，E在同一直线上，AB＝DE，∠B＝∠E，请添加一个条件，使得△ABC≌△DEF．添加的条件可以是 　 　（只需写一个，不添加辅助线）；

14．（3分）如图，在△ABC中，AD是BC边上的中线，若S△ABC＝12，AC＝3，则点D到AC的距离为 　 　．

15．（3分）如图，在△ABC中，将∠ABC对折，使AB和BC在同一直线上，折痕为BE，延长BE至点D，使得BD＝AB，连接CD，若∠A＝∠D，则∠1+∠2＝　 　°．

三．解答题（共8小题，满分75分）
16．（7分）计算下列各式
（1）m8÷m2﹣（3m3）2+2m2•m4；
（2）（﹣1）2021+（）﹣2+（3.14﹣π）0．
17．（8分）先化简，再求值：（a﹣2b）（a+2b）﹣（a﹣2b）2+8b2，其中a＝﹣6，b＝
18．（8分）在一个不透明的袋子中装有除颜色外都相同的黄球、绿球和红球共12个，其中红球有2个．
（1）摸到红球的概率是 　 　；
（2）若摸到绿球的概率是，求袋子中黄球的个数．
19．（8分）如图是由边长为1的小正方形组成的6×6网格，每个小正方形的顶点叫做格点，线段AB的两个顶点都是格点．仅用无刻度的直尺在给定网格中完成画图．
（1）在图1中以线段AB为边作一个锐角△ABC（点C在格点上），使其成为轴对称图形；
（2）在图2中以线段AB为腰作一个等腰直角△ABC，△ABC的面积为 　 　．

20．（10分）某数学兴趣小组把两个同样大小的含30°角的三角尺斜边重合水平放置，如图2所示，其中E是AD与BC的交点，F是AB的中点，请你探究CE，EF的数量关系，将下面的推理过程中横线空白处补充完整．
​
解：因为△ABC与△BAD是同样大小的含30°角的直角三角形（已知），
所以∠C＝∠D＝90°，∠CAB＝∠DBA＝60°，∠1＝∠2＝　 　°，
所以∠CAE＝∠CAB﹣∠2＝30°，
所以∠CAE＝∠2（等量代换），
即AD平分∠CAB（ 　 　），
在△ACE与△BDE中，
因为∠C＝∠D，∠CEA＝∠DEB（ 　 　），AC＝BD（已知），
所以△ACE≌△BDE（ 　 　），
所以AE＝　 　，
所以△AEB是等腰三角形（等腰三角形的定义），
又因为F是AB的中点，
所以 　 　（等腰三角形“三线合一”），
因为∠C＝90°，
所以CE⊥AC，
又因为∠CAE＝∠2，CE⊥AC，EF⊥AB，
所以 　 　（角平分线上的点到这个角两边的距离相等）．
21．（10分）1～6个月的婴儿生长发育非常快，他们的体重y（g）和月龄x（月）的关系可以用y＝a+700x来表示，其中a是婴儿出生时的体重．下面表格表示在1～6个月之间，这个婴儿的体重y与月龄x之间的关系．
月龄x/月
1
2
3
4
5
6
体重y/g
4200
4900
5600
6300
7000
7700
（1）上表反映的变化过程中，　 　是自变量，　 　是因变量；
（2）利用表中数据直接写出该婴儿体重y（g）和月龄x（月）之间的关系式为 　 　；
（3）若某婴儿出生时的体重为4000g，请计算该婴儿第6个月时体重是多少g？
22．（12分）若整数x，y，z满足x2+y2＝z2，则称z为x，y的平方和数．
例如：32+42＝52，则5为3，4的平方和数．
请你根据以上材料回答下列问题（以下每一横线上填一个数字）：
（1）数3，4的另一个平方和数为 　 　；
（2）5还可以是数 　 　，　 　的平方和数；
（3）若数x+1与y﹣2的平方和数是0，则x＝　 　，y＝　 　；
（4）已知13是数1﹣x与12的平方和数，求x的值．
23．（12分）“等面积法”是解决三角形内部线段长度的常用方法，如图1，在Rt△ABC中，∠BAC＝90°，作AH⊥BC，若AB＝4，AC＝3，BC＝5，可列式：AB•AC＝BC•AH，解得AH＝．
（1）在题干的基础上，
①如图2，点P为BC上一点，作PM⊥AB，PN⊥AC，设PM＝d1，PN＝d2，求证：4d1+3d2＝12；
②如图3，当点P在CB延长线上时，猜想d1、d2之间又有什么样的数量关系，请证明你的猜想；
（2）如图4，在△ABC中，AB＝AC＝10，BC＝12，S△ABC＝48，若点D是BC延长线上一点，且CD＝2，过点B作BE⊥BC，点P是直线BE上一动点，点Q是直线AC上一动点，连接PD、PQ，求DP+PQ的最小值．


参考答案与试题解析
一．选择题（共10小题，满分30分，每小题3分）
1． 解：32×37＝39．
故选：A．
2． 解：7nm用科学记数法表示为7×10﹣9．
故选：C．
3． 解：A、不是轴对称图形，不符合题意；
B、不是轴对称图形，不符合题意；
C、不是轴对称图形，不符合题意；
D、是轴对称图形，符合题意．
故选：D．
4． 解：A．根据同底数幂的乘法，a2•a3＝a5，那么A错误，故A不符合题意．
B．根据积的乘方，（﹣3a3）＝﹣27a3，那么B错误，故B不符合题意．
C．根据同底数幂的除法，a6÷a2＝a4，那么C错误，故C不符合题意．
D．根据积的乘方与幂的乘方，（﹣a2b）3＝﹣a6b3，那么D正确，故D符合题意．
故选：D．
5． 解：A、地球绕太阳公转，是必然事件，符合题意；
B、一个月有32天，是不可能事件，不符合题意；
C、一位射击运动员每次射击的命中环数，是随机事件，不符合题意；
D、任意买一张电影票，座位号是3的倍数，是随机事件，不符合题意．
故选：A．
6． 解：汽车经历：加速﹣匀速﹣减速至停止．
加速：速度增加；
匀速：速度保持不变；
减速：速度下降，到B地速度为0．
故选：A．
7． 解：由题意可得：（2vt+vt）÷（t+t）＝vt÷t＝v．
故选：D．
8． 解：由作法得DE垂直平分AB，
∴AE＝BE，DE⊥AB，
∴D点为AC的中点，
∴BD＝CD＝AD，
∴△BDC的周长＝BD+CD+BC＝AD+CD+BC＝AC+BC＝8+5＝13．
故选：C．
9． 解：由函数图象得：
A．4h时，甲品牌水杯水温较高，说法正确，故本选项不符合题意；
B．8h时，甲、乙两品牌水杯水温相同，说法正确，故本选项不符合题意；
C．甲、乙两品牌水杯水温都随着时间的增加而降低，说法正确，故本选项不符合题意；
D．8h以后，甲品牌水杯水温下降更快，原说法错误，故本选项符合题意．
故选：D．
10． 解：取CD的中点H，连接PH、FH，
∵四边形ABCD是长方形，F是AB的中点，
∴四边形ADHF是长方形，
∴FH＝AD＝AE+DE＝a+b；
由折叠可知：CD＝CF，
∵G是CF的中点，H是CE的中点，
∴CG＝CH，
在△GCP和△HCP中，
，
∴△GCP≌△HCP（SAS），
∴PG＝PH，
∴PF+PG＝PH+PF≥FH＝a+b，
∴当F、P、H三点共线时，PF+PG的值最小，最小值为：a+b．
故选：D．

二．填空题（共5小题，满分15分，每小题3分）
11． 解：原式＝2，
故答案为：2．
12． 解：根据题意得180°﹣30°＝150°，
故答案为：150．
13． 解：添加BF＝CE，
∵BF＝CE，
∴BF+FC＝CE+FC，
即BC＝EF，
在△ABC和△DEF中，
，
∴△ABC≌△DEF（SAS），
故答案为：BF＝CE（答案不唯一）．
14． 解：设点D到AC的距离为h，
∵AD是BC边上的中线，S△ABC＝12，
∴S△ACD＝S△ABC＝6，
∵AC＝3，
∴h×3＝6，解得h＝4．
故答案为：4．
15． 解：由折叠可知：∠ABE＝∠CBE，
∵∠A＝∠D，∠1＝∠CED，
∴∠ABD＝∠ACD＝∠CBD，
在△ABE和△DBC中，
，
∴△ABE≌△DBC（ASA），
∴BE＝BC，
∴∠BEC＝∠2，
∵∠1+∠BEC＝180°，
∴∠1+∠2＝180°，
故答案为：180．
三．解答题（共8小题，满分75分）
16． 解：（1）原式＝m6﹣9m6+2m6＝﹣6m6；
（2）原式＝﹣1+4+1＝4．
17． 解：原式＝a2﹣4b2﹣a2+4ab﹣4b2+8b2＝4ab，
当a＝﹣6，b＝时，原式＝﹣8．
18． 解：（1）摸到红球的概率＝＝；
故答案为；
（2）设袋子中黄球的个数为x个，
根据题意得＝，解得x＝2，
即袋子中黄球的个数为2个．
19． 解：（1）如图1，点C为所作；

（2）如图2，点C为所作，此时S△ABC＝5，
故答案为：5．
20． 解：因为△ABC与△BAD是同样大小的含30°角的直角三角形（已知），
所以∠C＝∠D＝90°，∠CAB＝∠DBA＝60°，∠1＝∠2＝30°，
所以∠CAE＝∠CAB﹣∠2＝30°，
所以∠CAE＝∠2（等量代换），
即AD平分∠CAB（角平分线的定义），
在△ACE与△BDE中，
因为∠C＝∠D，∠CEA＝∠DEB（对顶角的性质），AC＝BD（已知），
所以△ACE≌△BDE（AAS），
所以AE＝BE，
所以△AEB是等腰三角形（等腰三角形的定义），
又因为F是AB的中点，
所以EF⊥AB （等腰三角形“三线合一”），
因为∠C＝90°，
所以CE⊥AC，
又因为∠CAE＝∠2，CE⊥AC，EF⊥AB，
所以CE＝EF（角平分线上的点到这个角两边的距离相等）．
故答案为：30°，角平分线的定义，对顶角的性质，AAS，BE，EF⊥AB，CE＝EF．
21． 解：（1）由题意得，
上表反映的变化过程中，月龄x是自变量，体重y是因变量，
故答案为：月龄x，体重y；
（2）由题意得，
a+700×1＝4200，
解得a＝3500，
利用表中数据直接写出该婴儿体重y（g）和月龄x（月）之间的关系式为：y＝700x+3500，
故答案为：y＝700x+3500；
（3）若出生时体重为4000g，则体重和月龄之间的关系为：y＝4000+700x
当x＝6时，y＝4000+700×6＝8200（g），
答：该婴儿第6个月时体重是8200g．
22． 解：（1）∵32+42＝（﹣5）2，
∴数3，4的另一个平方和数为：﹣5，
故答案为：﹣5；
（2）∵02+52＝52，
∴5还可以是数0，5的平方和数，
故答案为：0；5（答案不唯一）；
（3）∵数x+1与y﹣2的平方和数是0，
∴（x+1）2+（y﹣2）2＝0，
∴x+1＝0，y﹣2＝0，
解得：x＝﹣1，y＝2，
故答案为：﹣1；2；
（4）∵13是数1﹣x与12的平方和数，
∴（1﹣x）2+122＝132，
整理得：（1﹣x）2＝25，
解得：x1＝6，x2＝﹣4．
23． （1）①证明：连接AP，
∵S△ABC＝S△ABP+S△ACP，
∴，
即：，
∴4d1+3d2＝12；

②解：猜想：3d2﹣4d1＝12，
理由如下：连接AP，
S△ACP﹣S△ABP＝S△ABC，
∴，
即：，
∴3d2﹣4d1＝12；


（2）解：如图，作点D关于直线BE的对称点D′，连接PD′，D′Q，过点D′作D′G⊥AC于点G；
∴D′P＝DP，
∴DP+PQ＝D′P+PQ≥D′Q，
∴当D′、P、Q三点共线且垂直AC时，DP+PQ最小，最小值为D′G；

连接AD′，过点A作AH⊥BC于点H，
∴＝48，
解得：AH＝8，
∵点D和D′关于直线BE对称，
∴BD′＝BD＝BC+CD＝14，
∵S△ABD′+S△ABC＝S△ACD′，
∴，
即：，
解得：D′G＝20.8，
即：DP+PQ最小值为20.8．