2023年江苏省连云港市赣榆区中考数学二模试卷（含解析）

这是一份2023年江苏省连云港市赣榆区中考数学二模试卷（含解析），共24页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。
2023年江苏省连云港市赣榆区中考数学二模试卷
一、选择题（本大题共8小题，共24.0分。在每小题列出的选项中，选出符合题目的一项）
1. 化简( 3)2的结果是(    )
A. −3 B. 3 C. ±3 D. 9
2. 在中国园林建筑中，洞窗是最生动的眼睛，主要以漏空图案填心为主，故也称镂空花窗.花窗图案丰富多样，以各种植物，动物，字体，几何图案和其他图案为基础，相互交错形成多种吉祥图案.则下列填心的图案中不是轴对称图形的是(    )
A. B. C. D.
3. 2023年的“五一”假日期间，连云港市迎来疫情后首个旅游高峰.据统计，连云港全市共接游客365.3万人次，实现旅游总收入5114000000元，其中“5114000000”用科学记数法表示为(    )
A. 5.114×108 B. 51.14×108 C. 5.114×109 D. 5.114×107
4. 已知正多边形的一个外角等于60°，则该正多边形的边数为(    )
A. 3 B. 4 C. 5 D. 6
5. 小红在“养成阅读习惯，快乐阅读，健康成长”读书大赛活动中，随机调查了本校初二年级20名同学，在近5个月内每人阅读课外书的数量，数据如下表所示：
人数
3
4
8
5
课外书数量(本)
12
13
15
18
则阅读课外书数量的中位数和众数分别是(    )
A. 35，15 B. 14，15 C. 13，18 D. 15，15
6. 如图，将一副三角板叠放在一起，使直角的顶点重合于点O，AB//OC，DC与OB交于点E，则∠DEO的度数为(    )
A. 85°
B. 70°
C. 75°
D. 60°
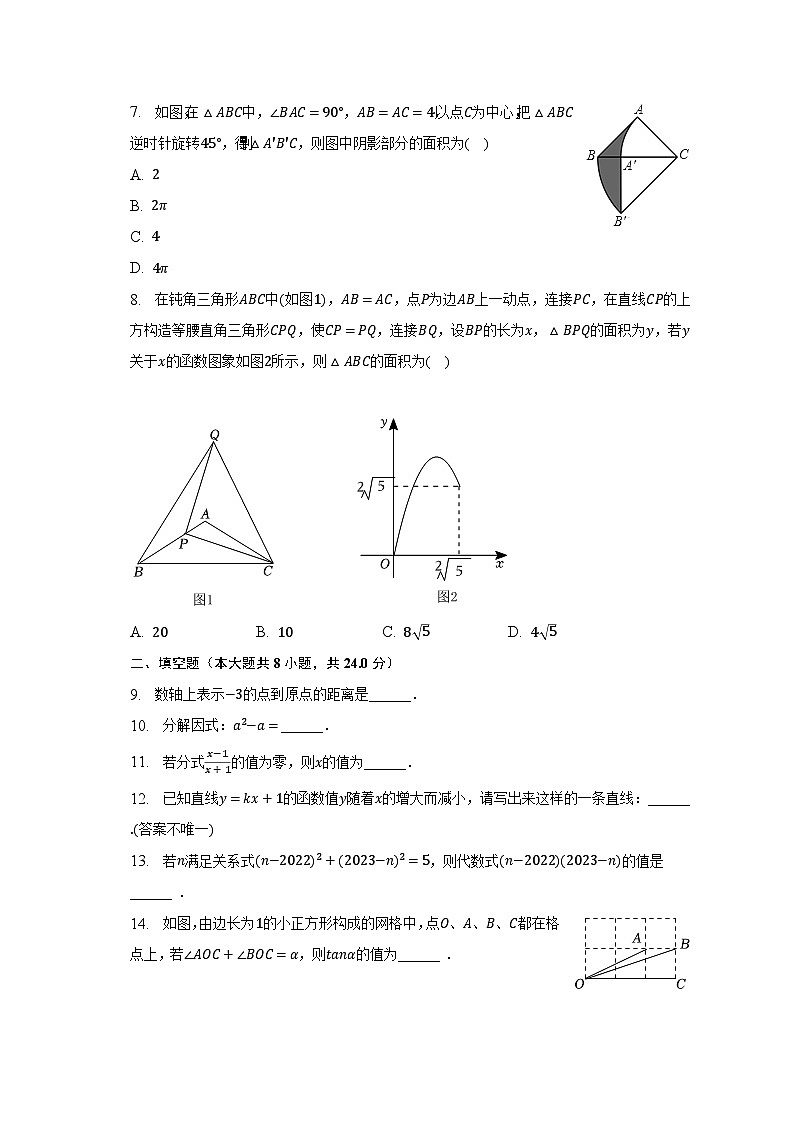
7. 如图，在△ABC中，∠BAC=90°，AB=AC=4，以点C为中心，把△ABC逆时针旋转45°，得到△A′B′C，则图中阴影部分的面积为(    )
A. 2
B. 2π
C. 4
D. 4π
8. 在钝角三角形ABC中(如图1)，AB=AC，点P为边AB上一动点，连接PC，在直线CP的上方构造等腰直角三角形CPQ，使CP=PQ，连接BQ，设BP的长为x，△BPQ的面积为y，若y关于x的函数图象如图2所示，则△ABC的面积为(    )


A. 20 B. 10 C. 8 5 D. 4 5
二、填空题（本大题共8小题，共24.0分）
9. 数轴上表示−3的点到原点的距离是______．
10. 分解因式：a2−a=______．
11. 若分式x−1x+1的值为零，则x的值为______．
12. 已知直线y=kx+1的函数值y随着x的增大而减小，请写出来这样的一条直线：______ .(答案不唯一)
13. 若n满足关系式(n−2022)2+(2023−n)2=5，则代数式(n−2022)(2023−n)的值是______ ．
14. 如图，由边长为1的小正方形构成的网格中，点O、A、B、C都在格点上，若∠AOC+∠BOC=α，则tanα的值为______ ．


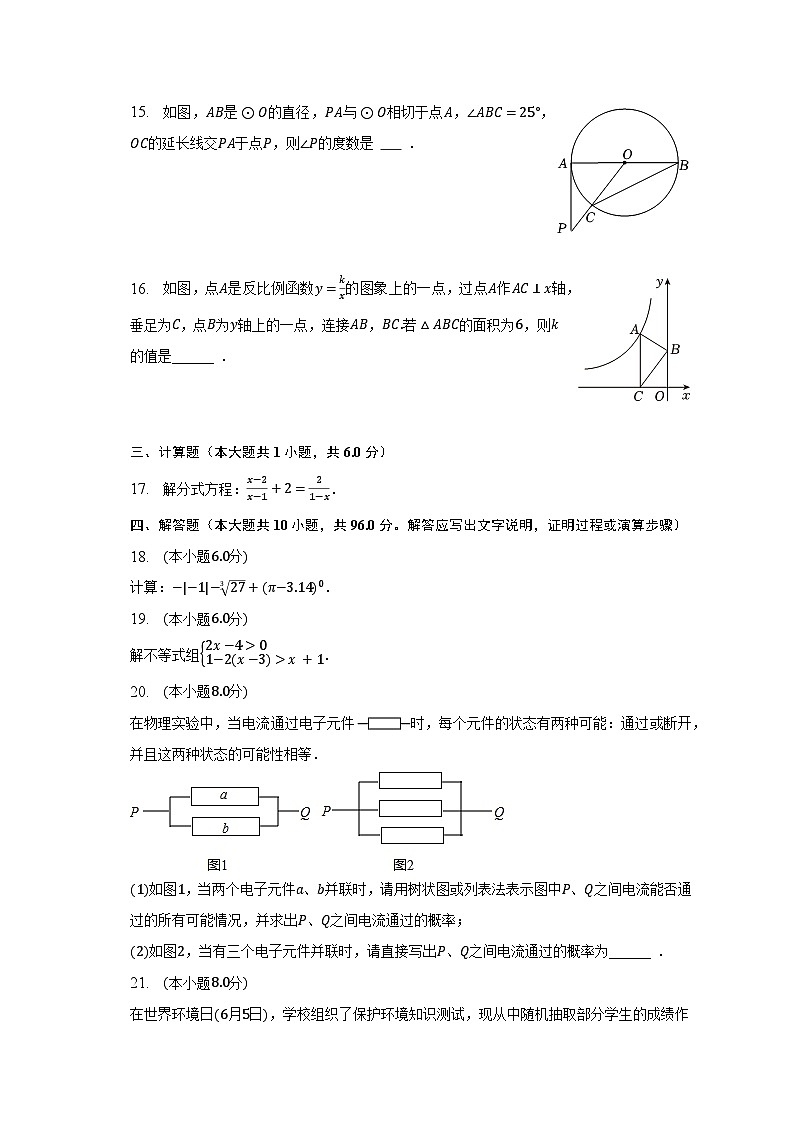
15. 如图，AB是⊙O的直径，PA与⊙O相切于点A，∠ABC=25°，OC的延长线交PA于点P，则∠P的度数是        ．


16. 如图，点A是反比例函数y=kx的图象上的一点，过点A作AC⊥x轴，垂足为C，点B为y轴上的一点，连接AB，BC.若△ABC的面积为6，则k的值是______ ．


三、计算题（本大题共1小题，共6.0分）
17. 解分式方程：x−2x−1+2=21−x．
四、解答题（本大题共10小题，共96.0分。解答应写出文字说明，证明过程或演算步骤）
18. (本小题6.0分)
计算：−|−1|−327+(π−3.14)0．
19. (本小题6.0分)
解不等式组2x−4>01−2(x−3)>x+1．
20. (本小题8.0分)
在物理实验中，当电流通过电子元件时，每个元件的状态有两种可能：通过或断开，并且这两种状态的可能性相等．

(1)如图1，当两个电子元件a、b并联时，请用树状图或列表法表示图中P、Q之间电流能否通过的所有可能情况，并求出P、Q之间电流通过的概率；
(2)如图2，当有三个电子元件并联时，请直接写出P、Q之间电流通过的概率为______ ．
21. (本小题8.0分)
在世界环境日(6月5日)，学校组织了保护环境知识测试，现从中随机抽取部分学生的成绩作为样本，按“优秀”“良好”“合格”“不合格”四个等级进行统计，绘制了如下尚不完整的统计图表．
测试成绩统计表
等级
频数(人数)
频率
优秀
30
a
良好
b
0.45
合格
24
0.20
不合格
12
0.10
合计
c
1
根据统计图表提供的信息，解答下列问题：
(1)表中a= ______ ，b= ______ ，c= ______
(2)补全条形统计图；
(3)若该校有800名学生参加了本次测试，估计测试成绩等级在良好以上(包括良好)的学生约有多少人？

22. (本小题10.0分)
如图，点B，E，C，F在一条直线上，AC与DE相交于点O，AB=DE，AB//DE，AC//DF．
(1)求证：△ABC≌△DEF；
(2)若∠B=55°，∠EOC=80°，求∠F的度数．

23. (本小题10.0分)
在学校开展“劳动创造美好生活”主题系列活动中，八年级(1)班负责校园某绿化角的设计、种植与养护．同学们约定每人养护一盆绿植，计划购买绿萝和吊兰两种绿植共46盆，且绿萝盆数不少于吊兰盆数的2倍．已知绿萝每盆9元，吊兰每盆6元．
(1)采购组计划将预算经费390元全部用于购买绿萝和吊兰，问可购买绿萝和吊兰各多少盆？
(2)规划组认为有比390元更省钱的购买方案，请求出购买两种绿植总费用的最小值．
24. (本小题10.0分)
动感单车是一种新型的运动器械．图①是一辆动感单车的实物图，图②是其侧面示意图．△BCD为主车架，AB为调节管，点A，B，C在同一直线上．已知BC长为70cm，∠BCD的度数为58°.当AB长度调至34cm时，求点A到CD的距离AE的长度(结果精确到1cm).(参考数据：sin58°≈0.85，cos58°≈0.53，tan58°≈1.60)

25. (本小题12.0分)
在平面直角坐标系中，已知一次函数y1=k1x+b与坐标轴分别交于A(5,0)，B(0,52)两点，且与反比例函数y2=k2x的图象在第一象限内交于P，Q两点，连接OP，△OAP的面积为54．
(1)求一次函数与反比例函数的表达式；
(2)当y2>y1时，请你直接写出x的取值范围；
(3)若C为线段OA上的一个动点，当PC+QC最小时，求△PQC的面积．

26. (本小题12.0分)
如图1，在矩形ABCD中，点E是边BC的中点，ABBE=k(k>1)，连接AE，过点E作EG⊥AE，并与矩形的外角∠DCF的平分线CG交于点G．

(1)求AEEG的值(用含k的代数式表示)；
(2)连接AG交CD于点H，连接EH，若∠AHE=90°，求k的值；
(3)如图2，当k与题(2)取相同值时，P为边CD上一点，连接AP、PG，当PG= 5，∠PAE=45°时，求BC的长．
27. (本小题14.0分)
在平面直角坐标系中，抛物线L1：y=ax2+x+c(a>0)与x轴交于A(−2,0)、B(1,0)两点，与y轴交于点C．
(1)求抛物线L1对应的函数表达式；
(2)如图1，点D为直线AC下方抛物线上的一动点，DM⊥AC于点M，DN//y轴交AC于点N，求线段DM的最大值和此时点D的坐标；
(3)如图2，将抛物线L1：y=ax2+x+c(a>0)沿着x轴向左平移后得到抛物线L2，若点P是抛物线L1与L2在x轴下方的交点且tan∠ACP=13，求抛物线L2对应的函数表达式．

答案和解析

1.【答案】B 
【解析】
【分析】
本题考查了二次根式的乘法，解答本题的关键是掌握二次根式的乘法法则： a⋅ b= ab．
按照二次根式的乘法法则求解．
【解答】
解：( 3)2= 3· 3= 9=3．
故选B．  
2.【答案】D 
【解析】解：A、是轴对称图形，不符合题意，
B、是轴对称图形，不符合题意，
C、是轴对称图形，不符合题意，
D、不是轴对称图形，符合题意，
故选：D．
根据轴对称图形的概念逐项判定即可．
本题考查了轴对称图形的定义，正确理解定义是解题的关键．

3.【答案】C 
【解析】解：5114000000=5.114×109．
故选：C．
科学记数法的表示形式为a×10n的形式，其中1≤|a|