数学七年级上册1.5.3 近似数获奖作业ppt课件

这是一份数学七年级上册1.5.3 近似数获奖作业ppt课件，文件包含153《近似数》教学课件pptx、153《近似数》分层作业解析版docx、153《近似数》教学设计docx、153《近似数》导学案docx、153《近似数》分层作业原卷版docx等5份课件配套教学资源，其中PPT共23页， 欢迎下载使用。
1.5.3 近似数 教学设计一、内容和内容解析1.内容本节课是人教版《义务教育教科书•数学》七年级上册（以下统称“教材”）第一章“有理数”1.5.3 近似数，内容包括：近似数的意义、精确度、四舍五入法求出近似数.2.内容解析近似数与准确数是日常生活中常见的两类数，近似数在实际问题中有着广泛的应用.教科书先以实例为基础介绍近似数和精确度的概念，然后结合对π用四舍五入法取近似值的方法，引导学生理解精确度和近似数的意义，最后通过例题让学生掌握按要求进行四舍五入取近似数的方法，通过旁注明确指出近似数末尾的0不能随意去掉，以期让学生明确一个近似数的精确程度主要看它的最末一个数字的数位.基于以上分析，确定本节课的教学重点为：近似数和精确度的意义.二、目标和目标解析1.目标(1)理解近似数的意义.(2)能按照精确度的要求，用四舍五入法求出近似数.（数感）2.目标解析近似数是指与准确数相接近的数.近似数通常因测量、估算，或用四舍五入等方法得到.近似数与准确数的接近程度，通常用精确度来刻画.一般地，一个近似数，四舍五入到哪一位，就说这个近似数精确到哪一位.如：…，结果取1，就叫精确到个位（或精确到1）；取1.3，就叫精确到十分位（或精确到0.1）；取1.33，就叫精确到百分位（或精确到0.01），等等.根据《课标》要求，初中学段学习近似数，不涉及有效数字，只说精确到哪一个数位.三、教学问题诊断分析近似数属于数与代数这一领域的内容.学生往往对近似数存在着一些生活经验，这些生活经验是学生学习的基础，但其中也有一些是错误的，备课和上课的过程中教师不要因为学生对近似数的知识不生疏，而使近似数的产生的过程，近似数的价值及如何求近似数等内容流于形式.必须让学生在正确区分准确数和近似数的基础上，明确近似数的角度有两种表示方式以及学会用“四舍五入”求近似值的方法.应该在交流的过程中让学生感受数据的实际意义，在自主学习的过程中体会近似数的意义，在探究讨论的过程中掌握了用四舍五入法求近似数的方法.教学中也及时了解学生的认知程度，以便调整教学.基于以上学情分析，确定本节课的教学难点为：由给出的近似数求其精确度，按给出的精确度求近似数.四、教学过程设计（一）情境引入下面有一段在博物馆的对话管理员：小姐，这个化石有800002年了.参观者：你怎么知道得这么精确？管理员：两年前，有位考古学家参观过这里，他说这个化石有80万年了.现在，两年过去了，所以就是800002年了.管理员的推断对吗？说说你的理由？（二）自学导航问题问题①：我们班在座的有_____位同学，其中男生有_____人, 女生有_____人.问题②：你的身高是______米，你的体重是______千克.大家想一想，上述的几个数据有什么不同？对于参加同一个会议的人数，有两个报道.一个报道说：“会议秘书处宣布，参加今天会议的有513人.”另一个报道说：“约有500人参加今天的会议.”思考：“513”和“500”哪个是准确的数据，哪个是近似的数据？（1）上面的数据，哪些是准确的？哪些是近似的？（2）举例说明生活中哪些数据是准确的，哪些数据是近似的？在许多情况下，很难取得准确数，或者不必使用准确数，而可以使用近似数. 例如，宇宙现在的年龄约为200亿年，长江长约6300km，圆周率π约为3.14，这里的数都是近似数.思考：什么样的数是近似数？1.我们得不到与实际完全相符的数，而是通过测量、估算得到的数都是近似数.例如，姚明的身高是2.26米.2.有时我们为了叙述、书写方便，通过四舍五入得到的数也是近似数.例如，2022年全国高考报名人数1193万人.（三）考点解析例1.下列各数中，是准确数的有_______，是近似数的有__________.(填序号)①绿化队今年植树约20000棵；②数学课本定价9.65元；③小强的身高约为1.6m；④王大伯家里养了8只鸡；⑤今天的气温最高约为24℃；⑥买门票估计需要1000元.解析:根据准确数和近似数的概念，抓住关键词判断.【迁移应用】1.下列各数，是准确数的是(   )A.小亮同学的身高是1.72m       B.小明同学买了6支铅笔C.教室的面积是60m2            D.小兰买了3kg西红柿2.给出下列数据:①某校学生有1237人；②小丽的体重大概为38kg；③食堂购进15袋土豆；④圆周率π约为3.14.其中是准确数的是_________，是近似数的是________. (填序号)（四）合作探究小明和小颖分别测量了同一片树叶的长度，他们所用的直尺的最小单位是不同的，分别是厘米和毫米.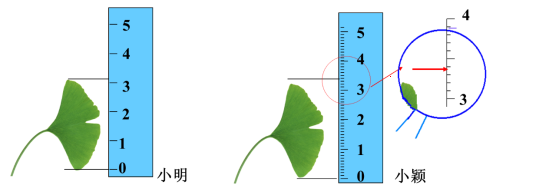问题：根据小明的测量，这片树叶的长度约为多少？根据小颖的测量呢？谁的测量结果会更精确一些？近似数与准确数的接近程度，可以用精确度表示.例如，前面的五百是精确到百位的近似数，它与准确数513的误差为13.说一说：小明、小颖的测量分别精确到什么单位？按四舍五入法对圆周率π取近似数，有π≈3（精确到个位），π≈3.1（精确到0.1，或叫做精确到十分位），π≈_____（精确到0.01，或叫精确到百分位），π≈3.140（精确到______，或叫做精确到______），π≈3.1416（精确到________，或叫做精确到_______），……（五）考点解析例2.用四舍五入法对下列各数取近似数:(1)0.0364(精确到0.001);        (2)14.046(精确到个位);(3)14.046(精确到0.1);          (4)21.3589(精确到百分位).解:(1)0.0364≈0.036;          (2)14.046≈14;   (3)14.046≈14.0;           (4)21.3589≈21.36. 思考：这里的14和14.0的精确度相同吗？表示近似数时，能简单地把14.0后面的0去掉吗？【迁移应用】1.用四舍五入法对0.06045取近似值,错误的是(   )A.0.1(精确到0.1)            B.0.06(精确到百分位)C.0.061(精确到千分位)       D.0.0605(精确到0.0001)2.近似数5.43精确到_______位.3.8.59015≈________(精确到0.001);12.34567≈______(精确到个位).例3.近似数3.70所表示的准确数a的取值范围是_________________.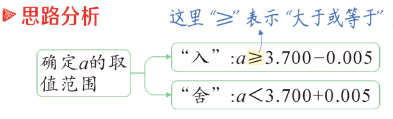【迁移应用】1.由四舍五入法得到的近似数是4.85,那么原数不可能是(   )A.4.8514      B.4.8496      C.4.8501       D.4.85662.已知a≈3.50是由四舍五入法得到的近似数,则a的取值范围是(   ) A.3.45≤a＜3.55           B.3.495≤a＜3.505C.3.495≤a≤3.505         D.3.495＜a＜3.505例4.用四舍五入法对下列各数取近似数或说明近似数的精确度:(1)12300000≈____________(精确到百万位);(2)近似数3.14×106精确到______位.解析: (1)12300000精确到百万位就是看数位2的下一位，如果≥5就进一，如果＜5就舍去；再用科学记数法表示即可.(2)近似数3.14×106精确到哪一位，先还原成原数，再看4处于哪一位.【迁移应用】1.某种鲸鱼的质量约为1.36×105kg,关于这个近似数，下列说法正确的是(    )A.它精确到百位             B.它精确到0.01C.它精确到千分位           D.它精确到千位2.2035≈___________(精确到百位).3.近似数2.245×104精确到______位.例5.填空.(1)29.45亿精确到_______位;(2)6.715万≈_______________(精确到百位).解析:(1)29.45亿精确到哪一位，先还原成原数，29.45亿=2945000000，再看5处于哪一位.(2)6.715万精确到百位，先还原成原数，6.715万=67150，就是看数位1的下一位，如果≥5就进一，如果＜5就舍去；再用科学记数法表示即可.【迁移应用】1.近似数3.59万精确到______位;2.近似数5.0310亿精确______位.3.46.0527亿≈_______________(精确到十万位).（六）小结梳理一、近似数：1.我们得不到与实际完全相符的数，而是通过测量、估算得到的数都是近似数.例如，姚明的身高是2.26米.2.有时我们为了叙述、书写方便，通过四舍五入得到的数也是近似数.例如，2022年全国高考报名人数1193万人.二、精确度：近似数与准确数的接近程度，可以用精确度表示.五、教学反思