资料中包含下列文件,点击文件名可预览资料内容










还剩52页未读,
继续阅读
成套系列资料,整套一键下载
人教版初中数学七年级上册 第一章 有理数 章节复习 课件+达标检测(含教师+学生版)
展开
这是一份人教版初中数学七年级上册 第一章 有理数 章节复习 课件+达标检测(含教师学生版),文件包含第一章有理数章节复习pptx、第一章有理数单元测试原卷版docx、第一章有理数单元测试解析版docx等3份课件配套教学资源,其中PPT共60页, 欢迎下载使用。
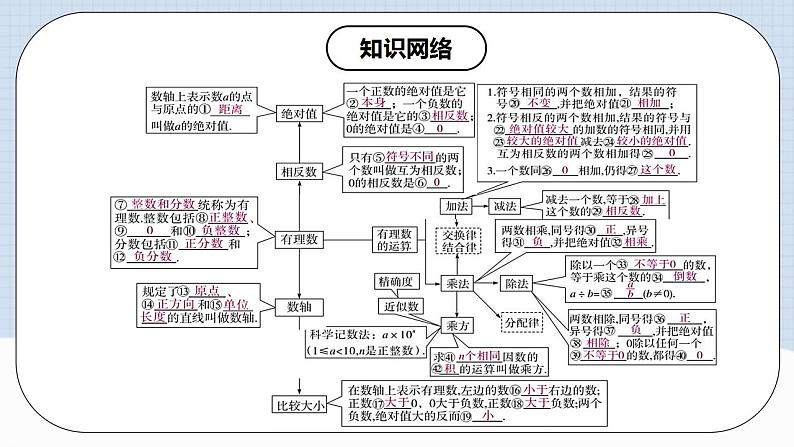
第一章 有理数 章节复习
人教版数学七年级上册
4.用正、负数表示具有相反意义的量.
一、正数和负数
1.像1,2,3,1.8%这样大于0的数叫做正数.
2.像-3,-1,-2,-2.7%这样在正数前面加上符号“-”(负)的数叫做负数.
3.0既不是正数,也不是负数.
5.具有相反意义的量应满足的条件:①必须是同类量,而且是成对出现的;②只要求意义相反,不要求数量一定相等.
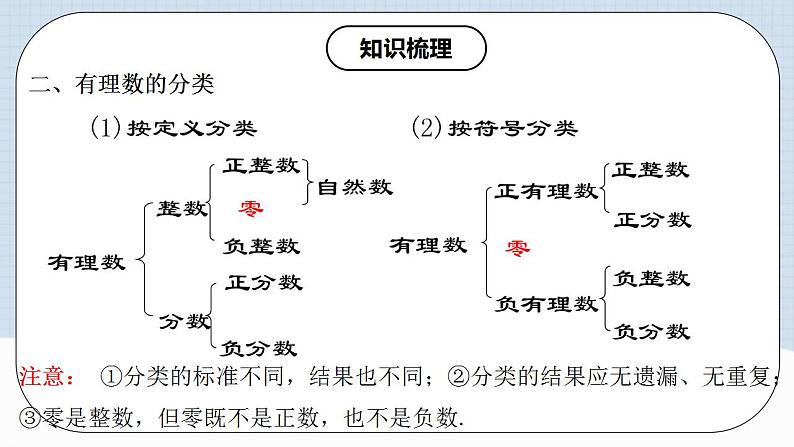
二、有理数的分类
注意: ①分类的标准不同,结果也不同;②分类的结果应无遗漏、无重复;③零是整数,但零既不是正数,也不是负数.
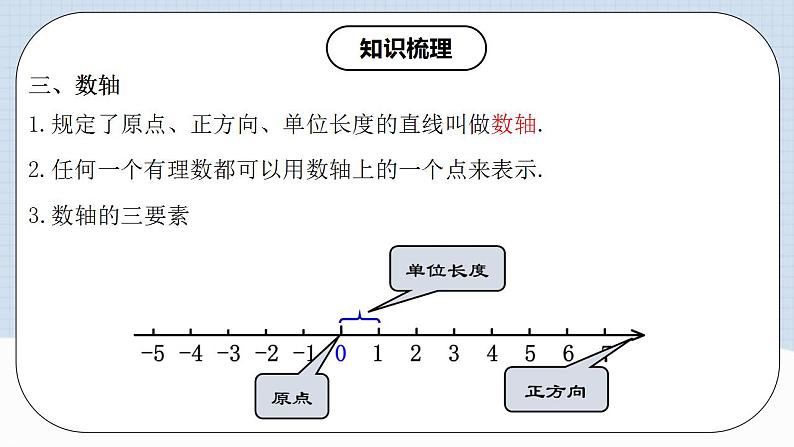
三、数轴
3.数轴的三要素
1.规定了原点、正方向、单位长度的直线叫做数轴.
2.任何一个有理数都可以用数轴上的一个点来表示.
数轴的画法:
1.画一条水平直线,定原点(如图),原点表示0.
2.规定从原点向右为正方向,那么相反的方向(从原点向左)则为负方向.
3.选择适当的长度为单位长度.(单位长度要一致)
三、数轴
(1)原点、单位长度和正方向三要素缺一不可;(2)直线一般画水平的;(3)正方向用箭头表示,一般取从左到右;(4)取单位长度应结合实际需要,但要做到刻度均匀.
画数轴注意事项:
三、数轴
位置特征:1.分居原点左右;2.到原点距离相等.
a的相反数是-a; 0的相反数是0
像2和-2,5和-5这样,只有符号不同的两个数叫做互为相反数.
一般地,设a是一个正数,数轴上与原点距离是a的点有两个,它们分别在原点左右,表示-a和a. 我们说这两点关于原点对称.
四、相反数
五、绝对值
1.定义:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,用“|a|”表示.
一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0. 即(1)如果 a>0,那么|a|=___;(2)如果 a=0,那么|a|=___;(3)如果 a<0,那么|a|=___.
a
-a
0
|a|≥0
2.绝对值的性质及应用
六、有理数大小的比较
有理数大小的比较方法2---数的相对大小比较法
一般地,正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
有理数大小的比较方法1---数轴比较法
在数轴上表示的两个数,右边的数总比左边的数大.
七、有理数的运算
有理数加法运算的基本解题思路:1.先判断类型(同号、异号等);2.再确定和的符号;3.最后进行绝对值的加减运算.
七、有理数的运算
(a+b)+c=a+(b+c)
a+b=b+a
1.加法交换律:在有理数加法中,两个数相加,交换加数的位置,和不变.
2.加法结合律:在有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
用字母表示为:
用字母表示为:
七、有理数的运算
有理数的减法法则是一个转化法则,减号转化为加号,同时要注意减数变为它的相反数,这样就可以用加法来解决减法问题.
七、有理数的运算
1.有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.任何数同0相乘,都得0.
2.几个不是零的数相乘,负因数的个数为
奇数时积为负数偶数时积为正数
3.几个数相乘若有因数为零则积为零.
4.有理数乘法的求解步骤:有理数相乘,先确定积的符号,再确定积的绝对值.
5.乘积是1的两个数互为倒数.
七、有理数的运算
法则二:两数相除,同号得正,异号得负,并把绝对值相除.0除以任何一个不等于0的数,都得0.
法则一:除以一个不等于0的数,等于乘这个数的倒数.
1.有理数除法法则:
2.有理数除法化为有理数乘法以后,可以利用有理数乘法的运算律简化运算.
3.乘除混合运算往往先将除法化为乘法,然后确定积的符号,最后求出结果(乘除混合运算按从左到右的顺序进行计算)
七、有理数的运算
3.乘方的符号法则:
(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数,负数的偶次幂是正数;(3)零的正整数次幂都是零.
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
2.组成要素
1.乘方的定义
七、有理数的运算
(1)看清运算,定运算顺序;
(2)根据特点,巧用运算律;
(3)选对法则,耐心计算.
2.有理数的加减乘除混合运算三步走:
【运算顺序】1.先乘方,再乘除,最后加减;2.同级运算,从左到右进行;3.如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
1.有理数的混合运算
我们可以把大于10的数记成a×10n的形式,其中a是整数数位只有一位的数(即1≤a<10), n是正整数.这种记数方法叫做科学记数法.
2.灵活运用科学计数法,注意解题技巧,总结解题规律.
八、科学记数法
九、近似数
1.近似数:
(1)我们得不到与实际完全相符的数,而是通过测量、估算得到的数都是近似数.例如,姚明的身高是2.26米.
(2)有时我们为了叙述、书写方便,通过四舍五入得到的数也是近似数.例如,2022年全国高考报名人数1193万人.
近似数与准确数的接近程度,可以用精确度表示.
2.精确度:
例1.我国是最早使用负数的国家.在我国著名的数学专著《九章算术》中,明确提出了“正负术”.如果盈利20元记作“+20元”,那么亏损30元记作( )A.-30元 B.30元 C.50元 D.-50元
解析:“盈利与亏损”是具有相反意义的量,依题意知“盈利”记作“+”,则“亏损”应记作“-”,故亏损30元记作“-30元”.
A
【1-1】如果+10%表示增加10%,那么-5%表示__________.【1-2】规定上午10时记为0,10时以前记为负,10时以后记为正,如果上午11时记为+1,那么上午7时应记为______.【1-3】在体育课的跳远比赛中,以2.00m为标准,若小东跳出了1.85m,记作-0.15m,那么小明跳了2.23m,可记作_______m;小红跳了2.00m,可记作_____m.
减少5%
-3
+0.23
0
正数集合:{ };负整数集合:{ };正分数集合:{ };负有理数集合:{ };非负整数集合:{ }.
-6,-1,…
0,2000,…
【2-1】下列说法中正确的有( )①整数就是正整数和负整数;②0是整数,但不是自然数;③分数包括正分数、负分数;④正数和负数统称为有理数;⑤一个有理数,它不是整数就是分数.A.1个 B.2个 C.3个 D.4个
B
整数集合:{ };正分数集合:{ };负有理数集合:{ };非负整数集合:{ };非正整数集合:{ }.
99,1,-1,-2025,0,…
99,1,0,…
-1,-2025,0,…
-9
0
-72
-18%
-0.618
3.8
A
A
C
1
1或-1
9
例4.有理数a,b在数轴上的位置如图所示,则下列选项正确的是( )A.a>b B.|a|>|b| C.-a>b D.a>-b
【4-1】有理数a,b在数轴上的对应点的位置如图所示,下列结论正确的是( )A.a>b B.|a|<|b| C.a>-b D.-a>b
D
【4-2】a,b是有理数,它们在数轴上的对应点的位置如图所示,把a,-a,b,-b按照从小到大的顺序排列为( )A.-b<-a<a<b B.-a<-b<a<bC.-b<a<-a<b D.-b<b<-a<a
C
>
>
>
<
C
D
>
>
>
<
例7.刘某蛋糕店在某一时段的销售情况如下,请分别完成下列问题:(1)该蛋糕店在某一周的销售中,盈亏情况如表(盈余为正,亏损为负,单位:元).表中星期五的盈亏数被墨水涂污了,请你算出星期五的盈亏数,并说明星期五是盈还是亏?盈亏是多少?(2)该蛋糕店去年1~3月平均每月盈利2万元,4~6月平均每月亏损1万元,7~8月平均每月亏损2万元,9~12月平均每月盈利4万元,则该蛋糕店去年总的盈亏情况如何?
(1)表中星期五的盈亏数被墨水涂污了,请你算出星期五的盈亏数,并说明星期五是盈还是亏?盈亏是多少?(2)该蛋糕店去年1~3月平均每月盈利2万元,4~6月平均每月亏损1万元,7~8月平均每月亏损2万元,9~12月平均每月盈利4万元,则该蛋糕店去年总的盈亏情况如何?
解:(1)根据表格可得,4580-(-228)-(-753)-420-(-120)-2000-1880=1381(元).因为1381是正数,所以星期五是盈利,盈利1381元.(2)记盈利为正,亏损为负,则2×3+(-1)×3+(-2)×2+4×4=15(万元).因为15是正数,所以该蛋糕店去年总共盈利15万元.
【7-1】某旅游景点在某天13:00的气温是5℃,此后气温持续下降,某时刻测得气温已经下降到-1℃.如果平均每4h气温下降3℃,那么此刻的时间是几点?
【7-2】某超市去年由于受物价上涨的影响,第一季度平均每月亏损1.2万元,第二季度在全体员工的努力下,平均每月盈利2.5万元,第三季度平均每月盈利2.1万元,第四季度平均每月亏损0.9万元.试通过计算说明这个超市去年总的盈亏情况.
解:记盈利为正,亏损为负,依题意得(-1.2)×3+2.5×3+2.1×3+(-0.9)×3=(-1.2+2.5+2.1-0.9)×3=7.5(万元).答:这个超市去年盈利7.5万元.
【7-3】在某次抗险救灾中,消防官兵的冲锋舟沿东西方向的河流营救灾民,早晨从A地出发,晚上到达B地,约定向东为正方向,当天的航行路程记录如下(单位:km):+15,-10,+9,-8,+14,-7,+11,-6.(1)通过计算说明B地在A地的什么方向,与A地相距多远?(2)救灾过程中,最远处离出发点A_____km;(3)若冲锋舟每千米耗油0.6L,油箱原有油量为40L,则途中还需补充多少升油?
解:(1)15-10+9-8+14-7+11-6=18(km),即B地在A地的东边18km处.(3)这一天航行的总路程为|+15|+|-10|+|+9|+|-8|+|+14|+|-7|+|+11|+|-6|=80(km),耗油量为80×0.6=48(L),所以还需补充的油量为48-40=8(L).答:途中还需补充8L油.
(1)通过计算说明B地在A地的什么方向,与A地相距多远?(2)救灾过程中,最远处离出发点A_____km;(3)若冲锋舟每千米耗油0.6L,油箱原有油量为40L,则途中还需补充多少升油?
24
例8.据相关研究,经过40min完全黑暗后,人眼对光的敏感性达到最高点,比黑暗前增加25000倍,将数据25000用科学记数法表示为( )A.25×103 B.2.5×104 C.0.25×105 D.0.25×106
B
【8-1】原子钟是以原子的规则振动为基础的各种守时装置的统称,其中氢脉泽钟的精度达到了1700000年误差不超过1s.数据1700000用科学记数法表示为______________.【8-2】据统计,地球上的海洋面积约为361000000km2,该数用科学记数法表示为3.61×10n,则n的值为_____.【8-3】根据国家统计局开展的“带动三亿人参与冰雪运动”调查报告数据显示,全国冰雪运动参与人数达到3.46亿人,成功实现了“三亿人参与冰雪运动”的宏伟目标.数3.46亿用科学记数法表示为_____________.
1.7×106
8
3.46×108
例9.(1)用四舍五入法将3.14159精确到千分位的结果是( )A.3.1 B.3.14 C.3.142 D.3.141(2)近似数3.70所表示的准确数a的取值范围是_________________.
C
3.695≤a<3.705
【9-1】用四舍五入法对0.06045取近似值,错误的是( )A.0.1(精确到0.1) B.0.06(精确到百分位)C.0.061(精确到千分位) D.0.0605(精确到0.0001)【9-2】已知a≈3.50是由四舍五入法得到的近似数,则a的取值范围是( ) A.3.45≤a<3.55 B.3.495≤a<3.505C.3.495≤a≤3.505 D.3.495<a<3.505【9-3】某种鲸鱼的质量约为1.36×105kg,关于这个近似数,下列说法正确的是( )A.它精确到百位 B.它精确到0.01C.它精确到千分位 D.它精确到千位
D
B
C
例1.下列说法正确的是( )A.正数和负数统称为有理数B.符号不同的两个数互为相反数C.绝对值等于本身的数只有正数D.互为倒数的两个数的乘积等于1
D
类型1:运算顺序不正确而出错
正解:原式=(-9)×(-3)×3-3=81-3=78.
类型2:运用分配律时漏乘某项出错
类型3:拆项造成的符号错误
类型4:乘方中对不同位置的负号的含义理解错误
类型1:数的正负性不确定而漏解
例6.已知|a|=12,|b|=7,则a+b=_______________.正解:因为|a|=12,所以a=12或a=-12.因为|b|=7,所以b=7或b=-7.当a=12,b=7时,a+b=19;当a=-12,b=-7时,a+b=-19;当a=12,b=-7时,a+b=5;当a=-12,b=7时,a+b=-5.故答案为19或-19或5或-5.
19或-19或5或-5
类型2:数轴上点的位置不确定而漏解
例7.在数轴上与表示-3的点相距10个单位长度的点表示的数是________.正解:当该点在表示-3的点的右侧时,-3+10=7;当该点在表示-3的点的左侧时,-3-10=-13.故答案为7或-13.
7或-13
例8.股民王先生上周五买进某公司股票1000股,每股18元,本周内每个交易日结束时该股票的涨跌情况如表(正数表示价格上涨,负数表示价格下跌,单位:元) :(1)周三结束时,该股票每股多少元?(2)对比本周内每个交易日结束时的每股股价,其中最高价和最低价分别是多少元?
解:(1)根据题意得18+3+2.5-4=19.5(元). 故周三结束时,该股票每股19.5元.(2)根据表格得周一每股价格为18+3=21(元),周二每股价格为21+2.5=23.5(元),周三每股价格为23.5-4=19.5(元),周四每股价格为19.5+2=21.5(元),周五每股价格为21.5-1.5=20(元).则其中的最高价是每股23.5元,最低价是每股19.5元.
第一章 有理数 章节复习
人教版数学七年级上册
4.用正、负数表示具有相反意义的量.
一、正数和负数
1.像1,2,3,1.8%这样大于0的数叫做正数.
2.像-3,-1,-2,-2.7%这样在正数前面加上符号“-”(负)的数叫做负数.
3.0既不是正数,也不是负数.
5.具有相反意义的量应满足的条件:①必须是同类量,而且是成对出现的;②只要求意义相反,不要求数量一定相等.
二、有理数的分类
注意: ①分类的标准不同,结果也不同;②分类的结果应无遗漏、无重复;③零是整数,但零既不是正数,也不是负数.
三、数轴
3.数轴的三要素
1.规定了原点、正方向、单位长度的直线叫做数轴.
2.任何一个有理数都可以用数轴上的一个点来表示.
数轴的画法:
1.画一条水平直线,定原点(如图),原点表示0.
2.规定从原点向右为正方向,那么相反的方向(从原点向左)则为负方向.
3.选择适当的长度为单位长度.(单位长度要一致)
三、数轴
(1)原点、单位长度和正方向三要素缺一不可;(2)直线一般画水平的;(3)正方向用箭头表示,一般取从左到右;(4)取单位长度应结合实际需要,但要做到刻度均匀.
画数轴注意事项:
三、数轴
位置特征:1.分居原点左右;2.到原点距离相等.
a的相反数是-a; 0的相反数是0
像2和-2,5和-5这样,只有符号不同的两个数叫做互为相反数.
一般地,设a是一个正数,数轴上与原点距离是a的点有两个,它们分别在原点左右,表示-a和a. 我们说这两点关于原点对称.
四、相反数
五、绝对值
1.定义:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,用“|a|”表示.
一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0. 即(1)如果 a>0,那么|a|=___;(2)如果 a=0,那么|a|=___;(3)如果 a<0,那么|a|=___.
a
-a
0
|a|≥0
2.绝对值的性质及应用
六、有理数大小的比较
有理数大小的比较方法2---数的相对大小比较法
一般地,正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
有理数大小的比较方法1---数轴比较法
在数轴上表示的两个数,右边的数总比左边的数大.
七、有理数的运算
有理数加法运算的基本解题思路:1.先判断类型(同号、异号等);2.再确定和的符号;3.最后进行绝对值的加减运算.
七、有理数的运算
(a+b)+c=a+(b+c)
a+b=b+a
1.加法交换律:在有理数加法中,两个数相加,交换加数的位置,和不变.
2.加法结合律:在有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
用字母表示为:
用字母表示为:
七、有理数的运算
有理数的减法法则是一个转化法则,减号转化为加号,同时要注意减数变为它的相反数,这样就可以用加法来解决减法问题.
七、有理数的运算
1.有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.任何数同0相乘,都得0.
2.几个不是零的数相乘,负因数的个数为
奇数时积为负数偶数时积为正数
3.几个数相乘若有因数为零则积为零.
4.有理数乘法的求解步骤:有理数相乘,先确定积的符号,再确定积的绝对值.
5.乘积是1的两个数互为倒数.
七、有理数的运算
法则二:两数相除,同号得正,异号得负,并把绝对值相除.0除以任何一个不等于0的数,都得0.
法则一:除以一个不等于0的数,等于乘这个数的倒数.
1.有理数除法法则:
2.有理数除法化为有理数乘法以后,可以利用有理数乘法的运算律简化运算.
3.乘除混合运算往往先将除法化为乘法,然后确定积的符号,最后求出结果(乘除混合运算按从左到右的顺序进行计算)
七、有理数的运算
3.乘方的符号法则:
(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数,负数的偶次幂是正数;(3)零的正整数次幂都是零.
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
2.组成要素
1.乘方的定义
七、有理数的运算
(1)看清运算,定运算顺序;
(2)根据特点,巧用运算律;
(3)选对法则,耐心计算.
2.有理数的加减乘除混合运算三步走:
【运算顺序】1.先乘方,再乘除,最后加减;2.同级运算,从左到右进行;3.如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
1.有理数的混合运算
我们可以把大于10的数记成a×10n的形式,其中a是整数数位只有一位的数(即1≤a<10), n是正整数.这种记数方法叫做科学记数法.
2.灵活运用科学计数法,注意解题技巧,总结解题规律.
八、科学记数法
九、近似数
1.近似数:
(1)我们得不到与实际完全相符的数,而是通过测量、估算得到的数都是近似数.例如,姚明的身高是2.26米.
(2)有时我们为了叙述、书写方便,通过四舍五入得到的数也是近似数.例如,2022年全国高考报名人数1193万人.
近似数与准确数的接近程度,可以用精确度表示.
2.精确度:
例1.我国是最早使用负数的国家.在我国著名的数学专著《九章算术》中,明确提出了“正负术”.如果盈利20元记作“+20元”,那么亏损30元记作( )A.-30元 B.30元 C.50元 D.-50元
解析:“盈利与亏损”是具有相反意义的量,依题意知“盈利”记作“+”,则“亏损”应记作“-”,故亏损30元记作“-30元”.
A
【1-1】如果+10%表示增加10%,那么-5%表示__________.【1-2】规定上午10时记为0,10时以前记为负,10时以后记为正,如果上午11时记为+1,那么上午7时应记为______.【1-3】在体育课的跳远比赛中,以2.00m为标准,若小东跳出了1.85m,记作-0.15m,那么小明跳了2.23m,可记作_______m;小红跳了2.00m,可记作_____m.
减少5%
-3
+0.23
0
正数集合:{ };负整数集合:{ };正分数集合:{ };负有理数集合:{ };非负整数集合:{ }.
-6,-1,…
0,2000,…
【2-1】下列说法中正确的有( )①整数就是正整数和负整数;②0是整数,但不是自然数;③分数包括正分数、负分数;④正数和负数统称为有理数;⑤一个有理数,它不是整数就是分数.A.1个 B.2个 C.3个 D.4个
B
整数集合:{ };正分数集合:{ };负有理数集合:{ };非负整数集合:{ };非正整数集合:{ }.
99,1,-1,-2025,0,…
99,1,0,…
-1,-2025,0,…
-9
0
-72
-18%
-0.618
3.8
A
A
C
1
1或-1
9
例4.有理数a,b在数轴上的位置如图所示,则下列选项正确的是( )A.a>b B.|a|>|b| C.-a>b D.a>-b
【4-1】有理数a,b在数轴上的对应点的位置如图所示,下列结论正确的是( )A.a>b B.|a|<|b| C.a>-b D.-a>b
D
【4-2】a,b是有理数,它们在数轴上的对应点的位置如图所示,把a,-a,b,-b按照从小到大的顺序排列为( )A.-b<-a<a<b B.-a<-b<a<bC.-b<a<-a<b D.-b<b<-a<a
C
>
>
>
<
C
D
>
>
>
<
例7.刘某蛋糕店在某一时段的销售情况如下,请分别完成下列问题:(1)该蛋糕店在某一周的销售中,盈亏情况如表(盈余为正,亏损为负,单位:元).表中星期五的盈亏数被墨水涂污了,请你算出星期五的盈亏数,并说明星期五是盈还是亏?盈亏是多少?(2)该蛋糕店去年1~3月平均每月盈利2万元,4~6月平均每月亏损1万元,7~8月平均每月亏损2万元,9~12月平均每月盈利4万元,则该蛋糕店去年总的盈亏情况如何?
(1)表中星期五的盈亏数被墨水涂污了,请你算出星期五的盈亏数,并说明星期五是盈还是亏?盈亏是多少?(2)该蛋糕店去年1~3月平均每月盈利2万元,4~6月平均每月亏损1万元,7~8月平均每月亏损2万元,9~12月平均每月盈利4万元,则该蛋糕店去年总的盈亏情况如何?
解:(1)根据表格可得,4580-(-228)-(-753)-420-(-120)-2000-1880=1381(元).因为1381是正数,所以星期五是盈利,盈利1381元.(2)记盈利为正,亏损为负,则2×3+(-1)×3+(-2)×2+4×4=15(万元).因为15是正数,所以该蛋糕店去年总共盈利15万元.
【7-1】某旅游景点在某天13:00的气温是5℃,此后气温持续下降,某时刻测得气温已经下降到-1℃.如果平均每4h气温下降3℃,那么此刻的时间是几点?
【7-2】某超市去年由于受物价上涨的影响,第一季度平均每月亏损1.2万元,第二季度在全体员工的努力下,平均每月盈利2.5万元,第三季度平均每月盈利2.1万元,第四季度平均每月亏损0.9万元.试通过计算说明这个超市去年总的盈亏情况.
解:记盈利为正,亏损为负,依题意得(-1.2)×3+2.5×3+2.1×3+(-0.9)×3=(-1.2+2.5+2.1-0.9)×3=7.5(万元).答:这个超市去年盈利7.5万元.
【7-3】在某次抗险救灾中,消防官兵的冲锋舟沿东西方向的河流营救灾民,早晨从A地出发,晚上到达B地,约定向东为正方向,当天的航行路程记录如下(单位:km):+15,-10,+9,-8,+14,-7,+11,-6.(1)通过计算说明B地在A地的什么方向,与A地相距多远?(2)救灾过程中,最远处离出发点A_____km;(3)若冲锋舟每千米耗油0.6L,油箱原有油量为40L,则途中还需补充多少升油?
解:(1)15-10+9-8+14-7+11-6=18(km),即B地在A地的东边18km处.(3)这一天航行的总路程为|+15|+|-10|+|+9|+|-8|+|+14|+|-7|+|+11|+|-6|=80(km),耗油量为80×0.6=48(L),所以还需补充的油量为48-40=8(L).答:途中还需补充8L油.
(1)通过计算说明B地在A地的什么方向,与A地相距多远?(2)救灾过程中,最远处离出发点A_____km;(3)若冲锋舟每千米耗油0.6L,油箱原有油量为40L,则途中还需补充多少升油?
24
例8.据相关研究,经过40min完全黑暗后,人眼对光的敏感性达到最高点,比黑暗前增加25000倍,将数据25000用科学记数法表示为( )A.25×103 B.2.5×104 C.0.25×105 D.0.25×106
B
【8-1】原子钟是以原子的规则振动为基础的各种守时装置的统称,其中氢脉泽钟的精度达到了1700000年误差不超过1s.数据1700000用科学记数法表示为______________.【8-2】据统计,地球上的海洋面积约为361000000km2,该数用科学记数法表示为3.61×10n,则n的值为_____.【8-3】根据国家统计局开展的“带动三亿人参与冰雪运动”调查报告数据显示,全国冰雪运动参与人数达到3.46亿人,成功实现了“三亿人参与冰雪运动”的宏伟目标.数3.46亿用科学记数法表示为_____________.
1.7×106
8
3.46×108
例9.(1)用四舍五入法将3.14159精确到千分位的结果是( )A.3.1 B.3.14 C.3.142 D.3.141(2)近似数3.70所表示的准确数a的取值范围是_________________.
C
3.695≤a<3.705
【9-1】用四舍五入法对0.06045取近似值,错误的是( )A.0.1(精确到0.1) B.0.06(精确到百分位)C.0.061(精确到千分位) D.0.0605(精确到0.0001)【9-2】已知a≈3.50是由四舍五入法得到的近似数,则a的取值范围是( ) A.3.45≤a<3.55 B.3.495≤a<3.505C.3.495≤a≤3.505 D.3.495<a<3.505【9-3】某种鲸鱼的质量约为1.36×105kg,关于这个近似数,下列说法正确的是( )A.它精确到百位 B.它精确到0.01C.它精确到千分位 D.它精确到千位
D
B
C
例1.下列说法正确的是( )A.正数和负数统称为有理数B.符号不同的两个数互为相反数C.绝对值等于本身的数只有正数D.互为倒数的两个数的乘积等于1
D
类型1:运算顺序不正确而出错
正解:原式=(-9)×(-3)×3-3=81-3=78.
类型2:运用分配律时漏乘某项出错
类型3:拆项造成的符号错误
类型4:乘方中对不同位置的负号的含义理解错误
类型1:数的正负性不确定而漏解
例6.已知|a|=12,|b|=7,则a+b=_______________.正解:因为|a|=12,所以a=12或a=-12.因为|b|=7,所以b=7或b=-7.当a=12,b=7时,a+b=19;当a=-12,b=-7时,a+b=-19;当a=12,b=-7时,a+b=5;当a=-12,b=7时,a+b=-5.故答案为19或-19或5或-5.
19或-19或5或-5
类型2:数轴上点的位置不确定而漏解
例7.在数轴上与表示-3的点相距10个单位长度的点表示的数是________.正解:当该点在表示-3的点的右侧时,-3+10=7;当该点在表示-3的点的左侧时,-3-10=-13.故答案为7或-13.
7或-13
例8.股民王先生上周五买进某公司股票1000股,每股18元,本周内每个交易日结束时该股票的涨跌情况如表(正数表示价格上涨,负数表示价格下跌,单位:元) :(1)周三结束时,该股票每股多少元?(2)对比本周内每个交易日结束时的每股股价,其中最高价和最低价分别是多少元?
解:(1)根据题意得18+3+2.5-4=19.5(元). 故周三结束时,该股票每股19.5元.(2)根据表格得周一每股价格为18+3=21(元),周二每股价格为21+2.5=23.5(元),周三每股价格为23.5-4=19.5(元),周四每股价格为19.5+2=21.5(元),周五每股价格为21.5-1.5=20(元).则其中的最高价是每股23.5元,最低价是每股19.5元.
相关资料
更多










