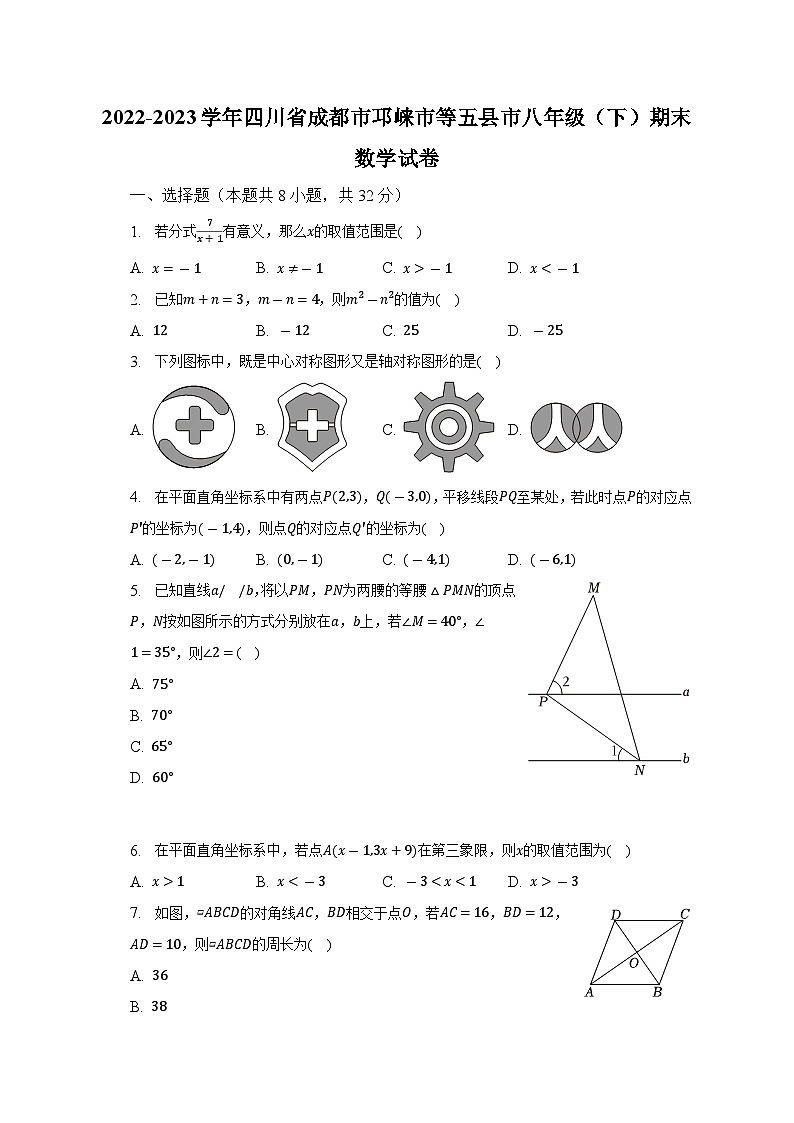
2022-2023学年四川省成都市邛崃市等五县市八年级（下）期末数学试卷（含解析）

这是一份2022-2023学年四川省成都市邛崃市等五县市八年级（下）期末数学试卷（含解析），共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年四川省成都市邛崃市等五县市八年级（下）期末数学试卷
一、选择题（本题共8小题，共32分）
1. 若分式7x+1有意义，那么x的取值范围是(    )
A. x=-1 B. x≠-1 C. x>-1 D. x1 B. x-1 
【解析】解：①若3a-1≥2a+3，即a≥4，
由(3a-1)⊕(2a+3)>-5知3a-1+2a+3>-5，
解得a>-75，
综上，a≥4；
②若3a-1-5，
解得a>-1，
综上，-1-1．
分3a-1≥2a+3、3a-10，
∴w随x的增大而增大，
∴当x=5时，w取得最小值，最小值=200×5+8000=9000，
∴租赁A型卡车5辆，B型卡车5辆时，租金总额最少，此时的租金总额为9000元． 
【解析】(1)根据A型卡车每天转运3000吨泥沙与B型卡车每天转运2700吨泥沙所需车辆数相同，可列出关于a的分式方程，解之经检验后，即可得出结论；
(2)①根据租车数量间的关系，可得出租赁B型卡车(10-x)辆，利用租金总额=每辆A型卡车每天的租金×租赁数量+每辆B型卡车每天的租金×租赁数量，可找出w关于x的函数关系式；
②根据“每天转运的泥沙不少于4750吨，租金总额不超过9600元”，可列出关于x的一元一次不等式组，解之可得出x的取值范围，结合x为正整数，可得出各租赁方案，再利用一次函数的性质，即可解决最值问题．
本题考查了分式方程的应用、一次函数的应用以及一元一次不等式组的应用，解题的关键是：(1)找准等量关系，正确列出分式方程；(2)①根据各数量之间的关系，找出w关于x的函数关系式；②根据各数量之间的关系，正确列出一元一次不等式组．

25.【答案】C 
【解析】解：(1)图1中，阴影部分可以看作两个正方形的面积差，即m2-n2，拼成长为(m+n)，宽为(m-n)的长方形，因此面积为(m+n)(m-n)，
因此m2-n2=(m+n)(m-n)，
故选：C；
(2)①设正方形ABCD的边长分别为a，正方形CEFG的边长为b，则S1=a2，S2=b2，
∵S1-S2=30，
∴a2-b2=30，
∴S不规则四边形BGED=S△BDG+S△EDG
=12DG⋅BC+12DG⋅CE
=12DG⋅(BC+CE)
=12(a-b)(a-b)
=12(a2-b2)
=12×30
=15，
答：不规则四边形BGED的面积为15；
②原式=(1-12)×(1+12)×(1-13)×(1+13)×(1-14)×(1+14)×…×(1-12022)×(1+12022)×(1-12023)×(1+12023)
=12×32×23×43×34×54×…×20212022×20232022×20222023×20242023
=12×20242023
=10122023．
(1)用代数式表示图1中阴影部分的面积即可；
(2)①设两个正方形的边长分别为a、b，用含有a、b的代数式表示不规则四边形BGED的面积即可；
②利用平方差公式将原式化为(1-12)×(1+12)(1-13)×(1+13)×(1-14)×(1+14)×…×(1-12022)×(1+12022)×(1-12023)×(1+12023)，进而得到12×32×23×43×34×54×…×20212022×20232022×20222023×20242023进行计算即可．
本题考查平方差公式的几何背景，掌握平方差公式的结构特征是正确解答的前提．

26.【答案】解：(1)由题意知，∠NDM=∠FDE=90°，
即∠NDF+∠FDM=∠MDE+FDM，
∴∠NDF=∠MDE，
在△DNF和△DME中，
DN=DM∠NDF=∠MDEDF=DE，
∴△DNF≌△DME(SAS)，
∴∠NFD=∠E，
在△EDF中，∠EDF=90°，DE=DF，
∴△EDF是等腰直角三角形，
∴∠E=∠DFE=45°，
∵∠EFN=∠NFD+∠DFE，
∴∠EFN=∠E+∠DFE=45°+45°=90°；
(2)MF2+NF2=2DM2，证明如下：
连接NF，

由(1)知，△DNF≌△DME，∠NFM=90°，
∴NF=ME，MF2+NF2=MN2，
∵DN⊥DM，DN=DM，
∴△MND是等腰直角三角形，
∴MN= 2DM，
∴MF2+NF2=( 2DM)2，
即MF2+NF2=2DM2；
(3)延长MF至N，且DM=DN，连接EN，DN，

∵∠DMF=45°，MD=5，
∴△MDN是等腰直角三角形，MN=5 2，
在△EDF中，∠EDF=90°，DE=DF，
∴△EDF是等腰直角三角形，
即∠NDF+∠FDM=∠NDE+FDN，
∴∠MDF=∠NDE，
在△DNE和△DMF中，
DN=DM∠NDE=∠MDFDE=DF，
∴△DNE≌△DMF(SAS)，
∴∠DNE=∠FMD=45°，NE=MF=2，
∵∠MND=45°，
∴∠MNF=∠MND+∠DNE=45°+45°=90°，
∴ME= MN2+NE2= (5 2)2+22=3 6． 
【解析】(1)根据SAS证△DNF≌△DME，得出∠NFD=∠E=45°，然后得出结论即可；
(2)连接NF，同理(1)得出△NFM是直角三角形，且NF=ME，再利用勾股定理得出线段间的关系即可；
(3)延长MF至N，且DM=DN，连接EN，同理(1)得出△NFM是直角三角形，利用勾股定理求出EM的长度即可．
本题主要考查三角形的综合题，熟练掌握全等三角形的判定和性质，等腰直角三角形，勾股定理等知识是解题的关键．