2023年安徽省安庆市中考数学二模试卷(含解析)
展开2023年安徽省安庆市中考数学二模试卷
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. 实数−2023的相反数是( )
A. −2023 B. −12023 C. 2023 D. 12023
2. 下列计算不正确的是( )
A. a2⋅a2=a4 B. (a2)3=a6 C. (2a2)3=6a6 D. a4÷(−a)2=a2
3. 魏晋南北朝时期,我国数学家祖冲之利用割圆术,求出圆周率π约为355113,其与π的误差小于0.00000027.其中0.00000027用科学记数法可表示为( )
A. 2.7×10−7 B. 0.27×10−6 C. 2.7×10−6 D. 2.7×107
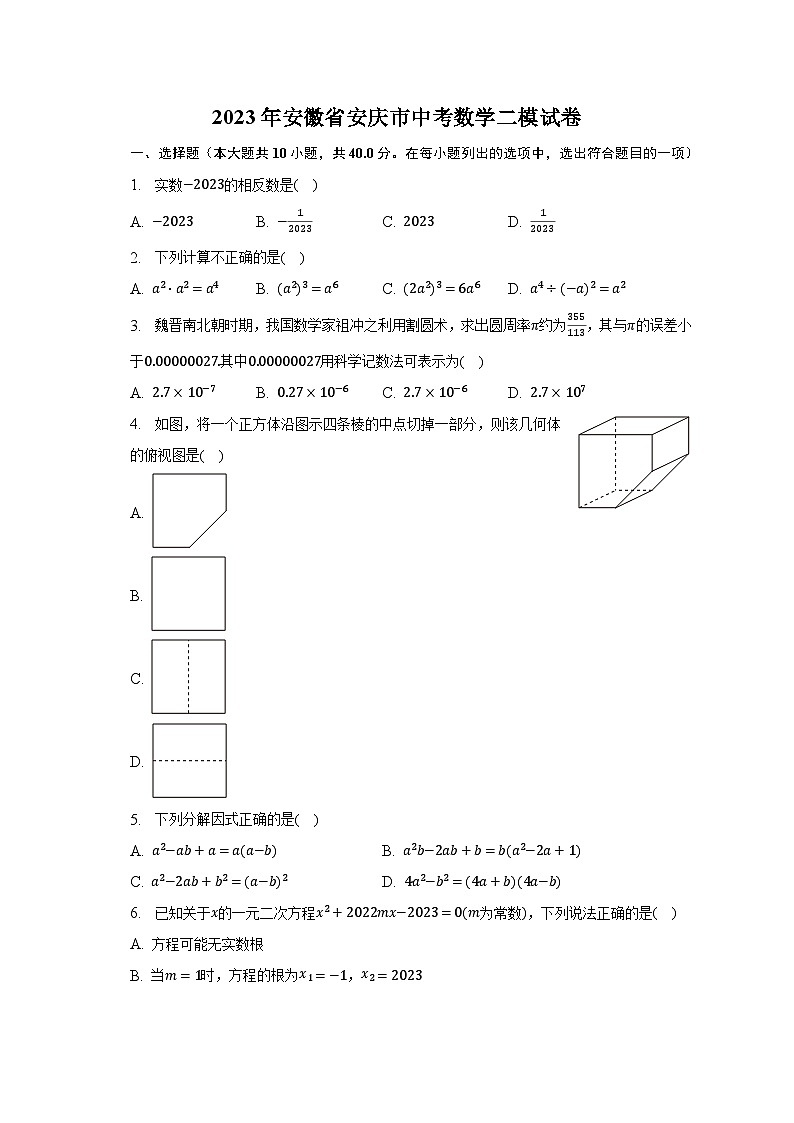
4. 如图,将一个正方体沿图示四条棱的中点切掉一部分,则该几何体的俯视图是( )
A.
B.
C.
D.
5. 下列分解因式正确的是( )
A. a2−ab+a=a(a−b) B. a2b−2ab+b=b(a2−2a+1)
C. a2−2ab+b2=(a−b)2 D. 4a2−b2=(4a+b)(4a−b)
6. 已知关于x的一元二次方程x2+2022mx−2023=0(m为常数),下列说法正确的是( )
A. 方程可能无实数根
B. 当m=1时,方程的根为x1=−1,x2=2023
C. 若x1,x2是方程的两个实数根,则x1⋅x2=2023
D. 当m=−1时,方程的根为x1=−1,x2=2023
7. 将一把直尺和一块含有30°的直角三角板按如图所示的位置摆放,若∠1=33°,则∠2为( )
A. 63°
B. 107°
C. 117°
D. 120°
8. 如图是某电路图,随机闭合开关S1,S2,S3中的任意2个,能同时使两盏小灯泡发光的概率是( )
A. 12
B. 13
C. 25
D. 23
9. 已知实数a,b,c满足a−3b+c=0,a+3b+c<0,则下列选项中正确的( )
A. b<0,b2−49ac≤0 B. b<0,b2−49ac≥0
C. b>0,b2−49ac≤0 D. b>0,b2−49ac≥0
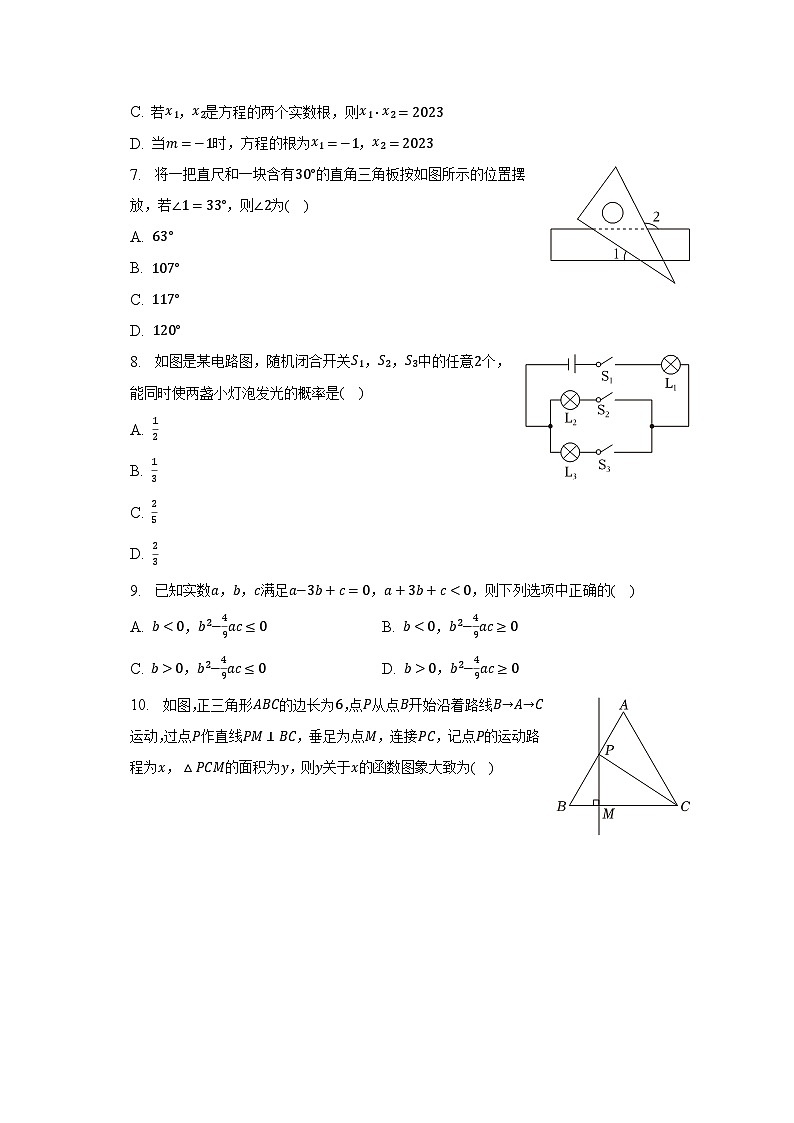
10. 如图,正三角形ABC的边长为6,点P从点B开始沿着路线B→A→C运动,过点P作直线PM⊥BC,垂足为点M,连接PC,记点P的运动路程为x,△PCM的面积为y,则y关于x的函数图象大致为( )
A.
B.
C.
D.
二、填空题(本大题共4小题,共20.0分)
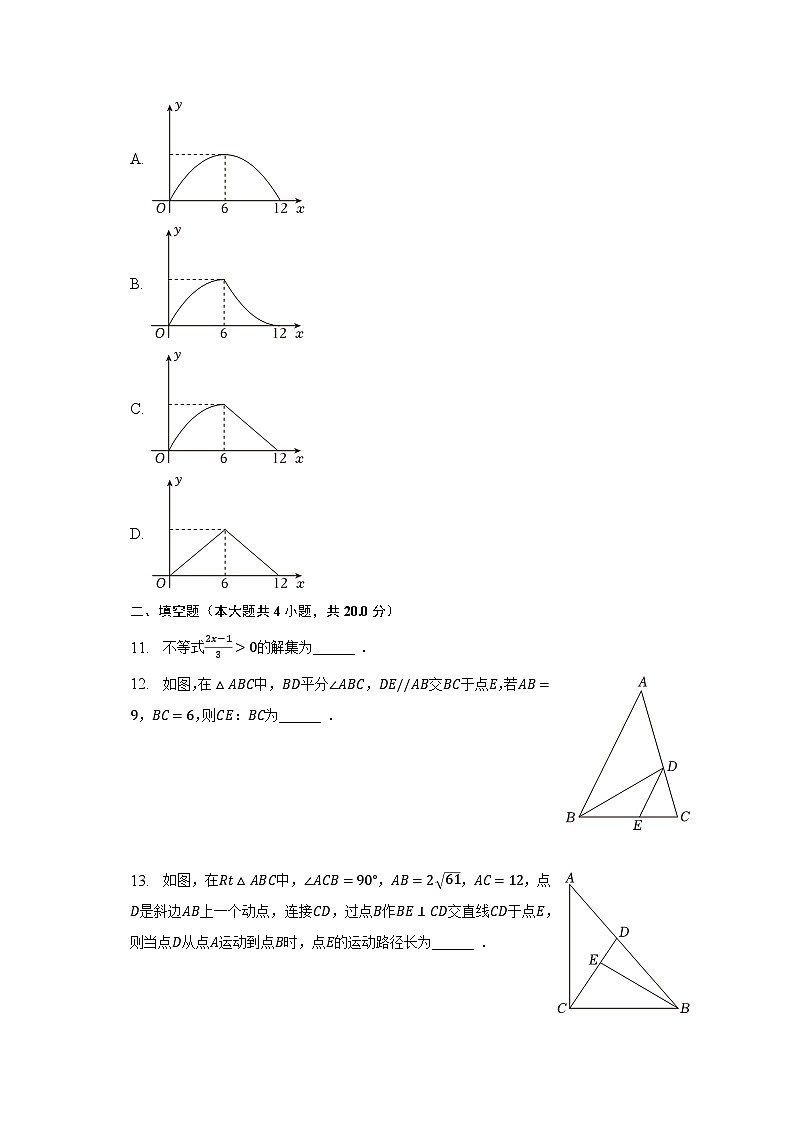
11. 不等式2x−13>0的解集为______ .
12. 如图,在△ABC中,BD平分∠ABC,DE//AB交BC于点E,若AB=9,BC=6,则CE:BC为______ .
13. 如图,在Rt△ABC中,∠ACB=90°,AB=2 61,AC=12,点D是斜边AB上一个动点,连接CD,过点B作BE⊥CD交直线CD于点E,则当点D从点A运动到点B时,点E的运动路径长为______ .
14. 已知抛物线C:y=x2+ax与直线AB:y=−x+2交于x轴上同一点.
(1)a的值为______ .
(2)点M是直线AB上的一个动点,将点M向左移动4个单位得到点N,若线段MN与抛物线C只有一个公共点,则点M的横坐标m的取值范围为______ .
三、解答题(本大题共9小题,共90.0分。解答应写出文字说明,证明过程或演算步骤)
15. (本小题8.0分)
计算:(−12)−2+|1− 3|− 12+(π−2023)0.
16. (本小题8.0分)
如图,在6×6的方格纸中,每个小正方形的边长为1,A,B,C,D,E均为格点,CD,BE交于点F,过A,B,F三点的圆如图所示,请利用无刻度直尺找出该圆的圆心O,并简要说明点O的位置是如何找到的(不要求证明).
17. (本小题8.0分)
2023年安庆市为成功创建国家卫生城市,青年志愿者决定义务清除重达75吨的垃圾.开工后,附近居民主动参与到该项义务劳动中来,使清除垃圾的速度提高了1倍,提前3小时完成了任务,求青年志愿者原计划每小时清除多少吨垃圾?
18. (本小题8.0分)
设一个两位数a3−可表示为10a+3,当a取不同的值时,a3−的平方如下:
第1个等式:13×13=169=(10×1+6)×10×1+9;
第2个等式:23×23=529=(10×2+6)×10×2+9;
第3个等式:33×33=1089=(10×3+6)×10×3+9;
…
(1)请写出第4个等式:______ ;
(2)根据上述规律,请写出a3−的平方的一般性规律,并予以证明.
19. (本小题10.0分)
如图,某班数学兴趣小组用无人机在操场上开展活动,此时无人机在离地面30米的D处,无人机测得操控者A的俯角为30°,测得点C处的俯角为45°.又经过人工测量得知操控者A和教学楼BC的水平距离AB为65.5米,则教学楼BC高度为多少米?(结果精确到米,)
20. (本小题10.0分)
已知反比例函数y=−2x与一次函数y=−x+b交于A,B两点,点B的纵坐标为−1.
(1)求一次函数解析式及与y轴交点C的坐标;
(2)若点A与点D关于原点对称,求△BCD的面积.
21. (本小题12.0分)
2022年9月开始,劳动课将正式成为中小学的一门独立课程,安庆市某中学提前尝试建立劳动教育实践基地,将劳动教育纳入日常教育教学中.某日,学校从七、八年级班级管理的花圃中,分别随机抽取了20个花圃对管理情况进行了评分(满分100分,数据分组为A组,90
(1)补全图①中的条形统计图;图②中C组所对应的圆心角为______ ;
(2)若八年级B组得分情况为89,88,87,87,86,85.
①八年级B组得分的方差为______ ;
②八年级20个花圃得分的中位数为______ 分;
(3)若90分以上为“五星花圃”,七、八年级各有200个花圃,估计七、八年级的花圃中“五星花圃”共多少个?
22. (本小题12.0分)
“龙池香尖”是怀宁县一款中国国家地理标志产品,素有:“扬子江心水,蒙山顶上茶”的美誉.某茶庄以600元/kg的价格收购一批龙池香尖,为保护消费者的合法权益,物价部门规定每千克茶叶的利润不低于0元,且不超过进价的60%,经过试销发现,日销量y(kg)与销售单价x(元/kg)满足一次函数关系,部分数据统计如表:
x(元/kg)
700
900
…
y(kg)
90
70
…
(1)根据表格提供的数据,求出y关于x的函数关系式.
(2)在销售过程中,每日还需支付其他费用9000元,当销售单价为多少时,该茶庄日利润最大,并求出最大利润.
23. (本小题14.0分)
正方形ABCD中,点P是对角线BD上一点,连接AP,过点P作AP的垂线分别交边AB,CD于E,F,交CB的延长线于点G,作PH⊥BD交AB于点H.
(1)求证:△APH≌△GPB;
(2)连接HF,AG.
①求证:四边形ADFH是矩形;
②如果点E是PG的中点,△AGE和△PDF的面积分别是S1,S2,求S1S2的值.
答案和解析
1.【答案】C
【解析】解:实数−2023的相反数是2023.
故选:C.
根据相反数的定义,即可解答.
本题考查了相反数,熟练掌握相反数的定义是解题的关键.
2.【答案】C
【解析】解:a2⋅a2=a2+2=a4,故选项A正确,不符合题意;
(a2)3=a2×3=a6,故选项B正确,不符合题意;
(2a2)3=8a6,故选项C错误,符合题意;
a4÷(−a)2=a4÷a2=a2,故选项D正确,不符合题意;
故选:C.
根据同底数幂的乘法法则判断A;根据幂的乘方法则判断B;根据积的乘方法则判断C,根据同底数幂的除法法则判断D.
本题考查了同底数幂的乘法与除法法则、幂的乘方、积的乘方法则,熟练区分同底数幂的乘法与积的乘方法则是本题的关键.
3.【答案】A
【解析】解:0.00000027=2.7×10−7,
故选:A.
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.据此可得出结果.
此题主要考查科学记数法的表示方法.正确确定a的值以及n的值是本题的关键.
4.【答案】C
【解析】解:从上面看几何体得到的平面图形是中间带虚线的正方形,
故选:C.
根据俯视图是从上面看几何体得到的平面图形即可解答.
本题考查了几何体的俯视图,理解俯视图的概念是解题的关键.
5.【答案】C
【解析】解:A、∵a2−ab+a=a(a−b+1),∴a2−ab+a=a(a−b)错误,故A项不符合题意;
B、∵a2b−2ab+b=b(a−1)2,∴a2b−2ab+b=b(a2−2a+1)错误,故B项不符合题意;
C、∵a2−2ab+b2=(a−b)2,∴a2−2ab+b2=(a−b)2正确,故C符合题意;
D、∵4a2−b2=(2a+b)(2a−b),∴4a2−b2=(4a+b)(4a−b)错误,故D项不符合题意;
故选:C.
根据分解因式的方法:提公因式法和公式法对每一项判断即可解答.
本题考查了因式分解的方法:提公因式和公式法,掌握完全平方式,平方差公式分解因式是解题的关键.
6.【答案】D
【解析】解:A、∵Δ=(2022m)2−4×1×(−2023)=(2022m)2+4×2023>0,
∴方程有两个不相等的实数根,故本选项不符合题意;
B、当m=1时,方程为x2+2022x−2023=0,即(x−1)(x+2023)=0,
方程的根为x1=1,x2=−2023,故本选项不符合题意;
C、若x1,x2是方程的两个实数根,则x1⋅x2=−2023,故本选项不符合题意;
D、当m=−1时,方程为x2−2022x−2023=0,即(x+1)(x−2023)=0,
方程的根为x1=−1,x2=2023,故本选项符合题意;
故选:D.
根据根的判别式可判断A;利用因式分解法解方程可判断B、D;利用根与系数的关系可判断C.
本题考查了根判别式,根与系数的关系,因式分解法解一元二次方程根,熟练掌握相关性质和定理是解决问题的关键.
7.【答案】C
【解析】解:∵EF//GH,
∴∠1=∠DAB,
∵∠1=33°,
∴∠DAB=33°,
∵∠C=30°,
∴∠ADC=180°−(∠C+∠DAB)=117°,
∴∠2=∠ADC=117°,
故选C.
根据直尺的两边平行得到∠1=∠DAC,再利用三角形内角和定理即可解答.
本题考查了平行线的性质,三角形内角和定理,对顶角相等,掌握三角形内角和定理是解题的关键.
8.【答案】D
【解析】解:画树状图得:
共有6种等可能的结果,其中能让两个灯泡发光的结果数为4,
∴能让灯泡L2发光的概率为:46=23.
故选:D.
画树状图,共有6种等可能的结果,能让两个灯泡发光的有4种,然后由概率公式求解即可.
本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.
9.【答案】B
【解析】解:由a−3b+c=0得a+c=3b,b=a+c3,
代入a+3b+c<0得3b+3b<0,
解得:b<0,
b2−49ac=(a+c3)2−49ac=(a−c)29≥0,
故选:B.
由a−3b+c=0得a+c=3b,代入a+3b+c<0可得b的取值范围,再把b=a+c3代入b2−49ac化简即可.
本题考查了代入消元法、完全平方式,解一元一次不等式,解题的关键是运用整体代入思想.
10.【答案】B
【解析】解:①点P在AB上,
∵正三角形ABC的边长为6,P的运动路程为x,
∴∠B=60°,AB=BC=AC=6,BP=x,
∴PM=sin∠B⋅x= 32x,MC=BC−cos∠B⋅x=6−x2,
∴S△PMC=12PM⋅MC=12× 32x⋅(6−x2)=− 38x2+3 32x,
∴− 38<0,
∴图象是一个开口向下的抛物线;
②点P在AC上时,
∵正三角形ABC的边长为6,P的运动路程为x,
∴∠C=60°,AB=BC=AC=6,CP=12−x,
∴PM=sin∠C⋅(12−x)= 32(12−x),MC=cos∠C⋅(12−x)=12(12−x),
∴S△PMC=12PM⋅MC=12× 32(12−x)×12×(12−x)= 38x2−3 3x+18 3,
∵ 38>0,
∴图象是一个开口向上的抛物线.
故选:B.
根据题意分别求出点P在AB上运动和点P在AC上运动的函数解析式即可解答.
本题考查了动点图象的问题,二次函数性质,二次函数的解析式,锐角三角函数,根据题意分清不同时间段图象和图形的对应关系是解题的关键.
11.【答案】x>12
【解析】解:2x−13>0,
去分母,得:2x−1>0,
移项,得:2x>1,
系数化为1,得x>12.
故答案为:x>12.
根据去分母,移项,系数化为1,求出不等式的解集即可.
本题主要考查了解一元一次不等式,熟练掌握运算步骤是解答本题的关键.
12.【答案】25
【解析】解:∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵DE//AB交BC于点E,
∴∠BDE=∠ABD,
∴BE=DE,
∵DE//AB交BC于点E,
∴DEAB=CEBC,
∵BC=6,
∴BE=DE=6−CE,
∵AB=9,
∴6−CE9=CE6,
∴CE=125,
∴CEBC=1256=25,
故答案为:25.
根据角平分线的定义及平行线的性质得到BE=DE,再根据平行线分线段成比例得到CE即可解答.
本题考查了角平分线的定义,平行线的性质,平行线分线段成比例,掌握平行线分线段成比例是解题的关键.
13.【答案】5π
【解析】解:∵BE⊥CD,
∴∠BEC=90°,
∴当点D从点A运动到点B时,点E的运动路径为BC为直径的半圆,
∵∠ACB=90°,AB=2 61,AC=12,
∴BC= AB2−AC2=10,
∴点E的运动路径长为12π×10=5π,
故答案为:5π.
求得∠BEC=90°,根据圆周角定理得到点E的运动路径为BC为直径的半圆,根据勾股定理求解即可.
本题主要考查了圆周角定理,勾股定理,说明点E的运动路径为BC为直径的半圆是解题的关键.
14.【答案】−2 2
把点(2,0)代入y=x2+ax得:4+2a=0,
解得:a=−2;
故答案为:−2;
(2)设M(a,−a+2),把点M向左移动4个单位得到点N(a−4,−a+2),
当抛物线C:y=x2+ax与直线MN只有一个交点时,
y=x2+ax的顶点坐标为(−a2,−a24),
顶点在直线MN上,则−a24=−a+2,
解得:原方程无实数解,此情况不成立;
当抛物线C:y=x2+ax与线段MN只有一个交点时,
f(a)⋅f(a−4)=2a2⋅[(a−4)2+a(a−4)]≤0,
解得:2≤a≤4,
当a=2,二次函数解析式为y=x2+2x,M(2,0),N(−2,0),
此时二次函数图象与线段MN有两个交点,此情况不成立,舍去;
当a=4,二次函数解析式为y=x2+4x,M(4,−2),N(0,−2),此情况成立.
故答案为:2
(2)设M(a,−a+2),把点M向左移动4个单位得到点N(a−4,−a+2),再分类讨论,当抛物线C:y=x2+ax与直线MN只有一个交点时,与当抛物线C:y=x2+ax与线段MN只有一个交点时,两种情况即可.
本题考查了二次函数的图象及性质,直线与二次函数的图象的交点情况,分类讨论思想方法是本题的关键.
15.【答案】解:(−12)−2+|1− 3|− 12+(π−2023)0
=4+(−1+ 3)−2 3+1
=4−1+ 3−2 3+1
=4− 3.
【解析】利用负整数指数幂,零指数幂,二次根式的性质,绝对值的化简的运算法则对各项进行计算,再依次进行计算即可.
本题考查了实数的混合运算,熟练掌握负整数指数幂,零指数幂,二次根式的性质,绝对值的化简的运算法则是解答本题的关键.
16.【答案】解:取格点G,直线AG交圆于点H,连接BH和AF的交点O即为圆心,
证明:∵BJ=AI=1,∠BJE=∠BIA=90°,BI=EJ=2,
∴Rt△BJE≌Rt△AIB(HL),
∴∠BEJ=∠ABI,
∵∠EBJ+∠BEJ=90°,
∴∠EBJ+∠ABI=90°,
∴∠ABF=90°,
则AF为圆O的直径;
同理可得∠BAH=90°,则BH为圆O的直径;
∴点O为圆心.
【解析】取格点G,直线AG交圆于点H,连接BH和AF的交点O即为圆心,利用全等三角形的判定和性质得到∠ABF=90°,∠BAH=90°,即可证明结论.
本题考查了圆周角定理,全等三角形的判定和性质,证明∠ABF=90°,∠BAH=90°是解题的关键.
17.【答案】解:设青年志愿者原计划每小时清除x吨垃圾,
根据题意得75x−752x=3,
解得x=12.5.
经检验x=12.5是原分式方程的根.
答:青年志愿者原计划每小时清除12.5吨垃圾.
【解析】设青年志愿者原计划每小时清除x吨垃圾,则后来每小时清除垃圾2x吨,根据“原工作时间−后来的工作时间=3”列分式方程即可.
本题主要考查分式方程的应用,解题的关键是理解题意,找到题目蕴含的相等关系,并据此列出方程求解.
18.【答案】43×43=1849=(10×4+6)×10×4+9
【解析】解:(1)第4个等式:43×4=1849=(10×4+6)×10×4+9;
故答案为:43×43=1849=(10×4+6)×10×4+9;
(2)a3−的平方的一般性规律为(a3−)2=(10n+3)2=(10n+6)×10n+9;
∵右边=(10n+3)2=(10n)2+60n+9,
左边=(10n+6)×10n+9=(10n)2+60n+9,
∴(10n+3)2=(10n+6)×10n+9成立.
故答案为:43×43=1849=(10×4+6)×10×4+9.
(1)根据题意写出第4个等式即可;
(2)根据规律写出第n个等式,利用完全平方公式和单项式乘多项式展开即可证明.
本题考查了规律型:数字的变化类:通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.也考查了完全平方公式.
19.【答案】解:过点D作DE⊥AB于点E,作CF⊥DE于点F,
由题可得:
AB=65.5,DE=30,∠A=30°,∠DCF=45°,
在Rt△ADE中,∠AED=90°,
∴tan30°=DEAE= 33,
∴AE=30 3,
∴BE=(65.5−30 3),
∵四边形BCFE是矩形,
∴CF=BE=65.5−30 3,
在Rt△DCF中,∠DFC=90°,
∴∠CDF=∠DCF=45°,
∴CF=DF=65.5−30 3,
∴BC=30−(65.5−30 3)=30 3−35.5≈16.5米.
答:教学楼BC高度为16.5米.
【解析】作DE⊥AB于点E,作CF⊥DE于点F,由tan30°=DEAE= 33得AE=30 3米,求得BE=(65.5−30 3),在Rt△DCF中,求得CF=DF=65.5−30 3,据此即可求解.
本题主要考查了解直角三角形的应用中仰角俯角问题,根据题意构造直角三角形是解题的关键.
20.【答案】解:(1)∵点B的纵坐标为−1,且点B在反比例函数y=−2x的图象上,
∴−1=−2x,
解得x=2,
∴点B的坐标为(2,−1),
∵点B在一次函数y=−x+b的图象上,
∴−1=−2+b,
解得b=1,
∴一次函数解析式为y=−x+1,
令x=0,则y=1,
∴点C的坐标为(0,1);
(2)联立y=−2xy=−x+1,
解得x=2y=−1或x=−1y=2,
∴点A的坐标为(−1,2),
∵点A与点D关于原点对称,
∴点D的坐标为(1,−2),
设直线BD的解析式为y=mx+n,
则2m+n=−1m+n=−2,解得m=1n=−3,
∴直线BD的解析式为y=x−3,
延长BD交y轴于点E,则点E的坐标为(0,−3),
∴CE=1−(−3)=4,
∴△BCD的面积为12×4×2−12×4×1=4−2=2.
【解析】(1)由点B的纵坐标为−1,求得点B的坐标为(2,−1),再代入y=−x+b,求得一次函数解析式,令x=0,则y=1,即可求得点C的坐标;是
(2)联立函数解析式,求得点A的坐标,得到点D的坐标,利用待定系数法求得直线BD的解析式为y=x−3,延长BD交y轴于点E,求得点E的坐标为(0,−3),利用三角形面积的和差即可求解.
本题考查了反比例函数图象与一次函数图象的交点问题,待定系数法求函数解析式,根据题意求出点A、D的坐标是解题的关键.
21.【答案】72° 53 86.5
【解析】解:(1)由图①可知,七年级管理的花圃中,评分B组的个数为20−2−6−4=8,
故可补画条形统计图如下:
由图②可知,八年级班级管理的花圃中,评分C组的占比为1−40%−30%−1%=20%,
故C部分所占的圆心角为360°×20%=72°.
故答案为:72°;
(2)①由题意可知,B组得分的平均数为:x−=89+88+87×2+86+856=87,
故方差为s2=16×[(89−87)2+(88−87)2+2×(87−87)2+(86−87)2+(85−87)2]=53;
②由题意可知,八年级20个花圃得分情况为:A组20×40%=8个,
若将20个数据按从小到大排列,其中中位数为第10、11两个分数的平均数,即B组中86和87两个分数的平均数,
所以八年级20个花圃得分的中位数为86+872=86.5.
故答案为:①53;②86.5;
(3)抽查的七年级管理的花圃得分在9(0分)以上的有3个,抽查的八年级管理的花圃得分在9(0分)以上的有8个,
所以可估计七、八年级各200个花圃中“五星花圃”的数量为:400×3+820+20=110个.
(1)根据条形统计图和扇形统计图分析计算即可;
(2)①根据给定的数据先计算B组得分的平均值,再利用方差计算公式计算即可;
②根据扇形统计图分别计算评分为A、B、C、D四组花圃个数,确定按从小到大排列后第10、11两个数据的值,再根据中位数的求法计算即可;
(3)先分别计算抽查的七、八年级管理的花圃得分在9(0分)以上数量,再根据抽查的得分在9(0分)以上的花圃数量与抽查总数的比值估算七、八年级200个花圃中“五星花圃”的数量.
本题主要考查了条形统计图和扇形统计图、方差、中位数的知识以及利用样本所占百分比估计总体的数量的知识,解题关键是熟练掌握相关概念及计算方法.
22.【答案】解:(1)设一次函数的关系式为y=kx+b,
把(700,90)和(900,70)代入得,
90=700k+b70=900k+b,
解得k=−110b=160,
y=−110x+160,
∵600×(1+60%)=960(元/kg),
∴y关于x的函数关系式y=−110x+160(600≤x≤960);
(2)根据题意,设茶庄日利润为W,
W=(x−600)y−9000,
=(x−600)(−110x+160)−9000
=−110x2+220x−105000,
=−110(x−1100)2+16000,
∵−110<0,600≤x≤960,
∴x=960时,W最大,最大值为−110(960−1100)2+16000=14040(元),
答:当销售单价是960元时,该茶庄利润最大,最大利润为14040元.
【解析】(1)设一次函数的关系式为y=kx+b,用待定系数法求解即可;
(2)设茶庄日利润为W,根据总利润=每千克茶叶的利润×日销量,得到二次函数,进而求出二次函数的最值即可.
本题考查了一次函数和二次函数的性质在实际生活中的应用,最大利润的问题常用函数的增减性来解决,确定变量,建立函数模型,然后结合实际选择最优方案是解答本题的关键.
23.【答案】(1)证明:在正方形ABCD中,∠ABD=45°,∠ABC=90°,
过点P作AP的垂线,PH⊥BD,
△BPH是等腰直角三角形,
∴PH=PB,∠PBH=∠PHB=45°,
∴∠PHA=∠PBG=135°
∵∠APH+∠HPE=90°,∠BPG+∠HPE=90°,
∴∠APH=∠BPG,
∴△APH≌△GPB(AAS);
(2)①证明:过点P作MN//BC交AB于点M,交CD于点N,过点F作FJ⊥CD交BD于点J,连FH,
∴∠PMB=∠PND=90°,∠ABD=∠CDB=45°,AB=BC,
∴△PMB是等腰直角三角形
∴PM=MB,∴AM=PN,∠PMA=∠PND=90°,
∵∠PAM+∠APM=90°,∠NPF+∠APM=90°,
∠PAM=∠FPN,
∴△AMP≌△PNF(AAS),
∴PA=PF=PG,∠BPG=∠FPD,
∵JF//BG,
∴∠G=∠PFJ,
∴△PBG≌△PJF(AAS),
BG=JF,
∵△DFJ是等腰直角三角形,
∴DF=FJ,
∵BG=AH,
∴AH=DF,AH//DF,∠BAD=90°,
四边形ADFH是平行四边形,
∵∠BAD=90°
∴四边形ADFH是矩形;
②解:
△AEG的高为BG,△DFP的底为DF,
∵BG=DF,
S△AEGS△PDF=12AE⋅BG12DF⋅PN=AEPN,
设BG=DF=a,
∵PM//BG,PE=GE,
∴BG=PM=a,EM=BE=12a,PM=FN=a,DN=PN=2a,
∴AM=2a,AE=52a,
S△AEGS△PDF=AEPN=52a2a=54,
S1S2=54.
【解析】(1)过点P作AP的垂线,先证明△BPH是等腰直角三角形,再证明△APH≌△GPB(AAS)即可;
(2)①过点P作MN//BC交AB于点M,交CD于点N,过点F作FJ⊥CD交BD于点J,先证明△AMP≌△PNF(AAS),再证明△PBG≌△PJF(AAS)即可;②先证明BG=DF,再证明S△AEGS△PDF=12AE⋅BG12DF⋅PN=AEPN,设BG=DF=a,求出AEPN即可.
本题考查了正方形的性质,全等三角形的性质和判定,等腰直角三角形的性质和判定,矩形的性质和判定,综合性质较强,题目难度较大.通过作辅助线得出全等三角形是解题的关键.
2023年安徽省安庆市太湖县望天学校中考数学三模试卷(含解析): 这是一份2023年安徽省安庆市太湖县望天学校中考数学三模试卷(含解析),共21页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2023年安徽省安庆市七校联盟中考数学一模试卷(含解析): 这是一份2023年安徽省安庆市七校联盟中考数学一模试卷(含解析),共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年安徽省安庆市中考数学一模试卷(含解析): 这是一份2023年安徽省安庆市中考数学一模试卷(含解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












