河北省沧州市献县2022-2023学年九年级上学期期末数学试题（含答案）

这是一份河北省沧州市献县2022-2023学年九年级上学期期末数学试题（含答案），共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
献县2022-2023学年度第一学期期末教学质量监测
九年级数学试题
一、选择题（本大题共16个小题，小题，每小题3分；小题，每小题2分，共42分。）
1.关于的方程是一元二次方程，则满足的条件是（ ）
A. B. C. D.
2.对二次函数的说法错误的是（ ）
A.开口向下 B.最大值为
C.顶点 D.时，随的增大而增大
3.下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A. B. C. D.
4.已知和的半径分别是和，且，则这两圆的位置关系是（ ）
A.内切 B.相交 C.外离 D.外切
5.为了防止输入性“新冠肺炎”，某医院成立隔离治疗发热病人防控小组，决定从内科3位骨干医师中（含有甲）抽调2人组成.则甲一定会被抽调到防控小组的概率是（ ）
A. B. C. D.
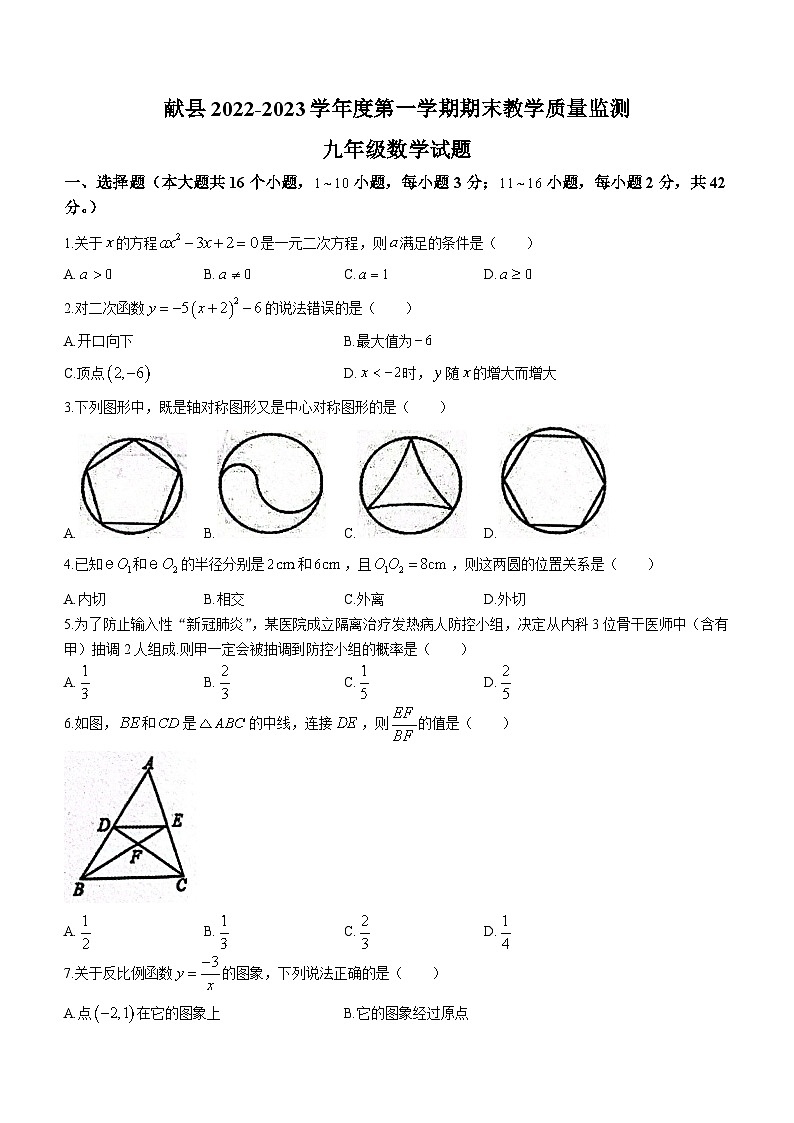
6.如图，和是的中线，连接，则的值是（ ）

A. B. C. D.
7.关于反比例函数的图象，下列说法正确的是（ ）
A.点在它的图象上 B.它的图象经过原点
C.它的图象在第一、三象限 D.当时，随的增大而增大
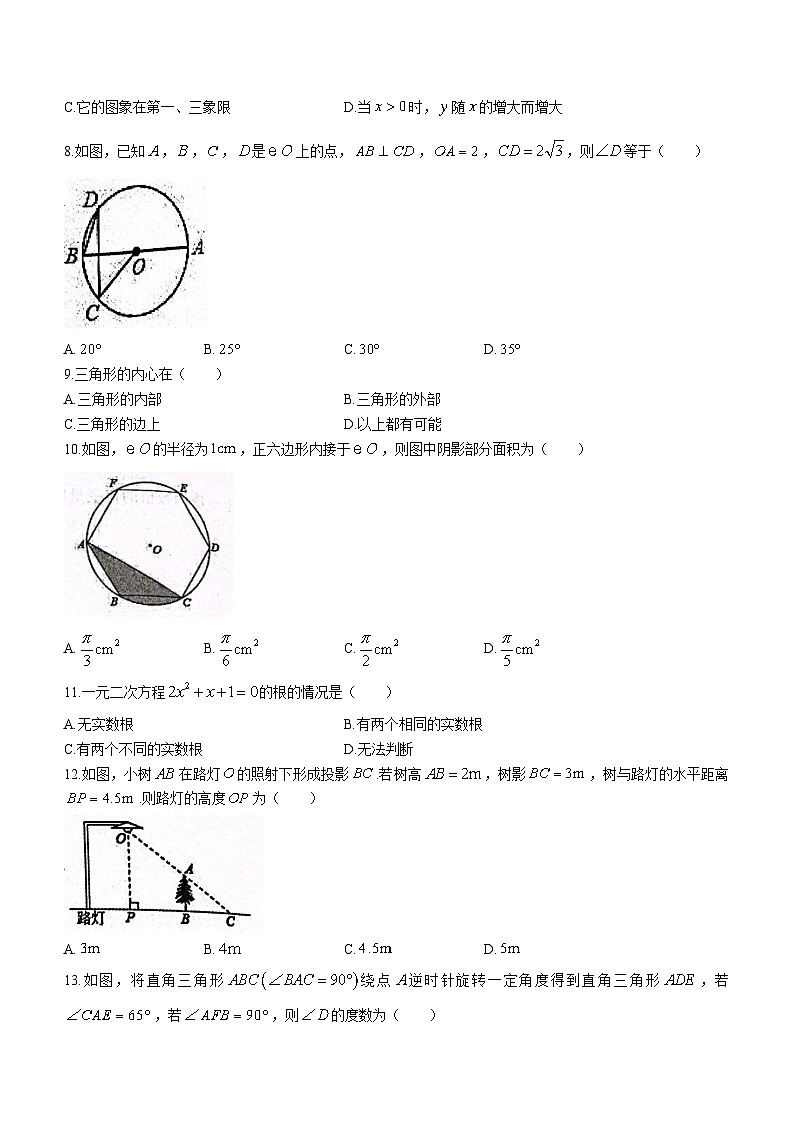
8.如图，已知，，，是上的点，，，，则等于（ ）

A. B. C. D.
9.三角形的内心在（ ）
A.三角形的内部 B.三角形的外部
C.三角形的边上 D.以上都有可能
10.如图，的半径为，正六边形内接于，则图中阴影部分面积为（ ）

A. B. C. D.
11.一元二次方程的根的情况是（ ）
A.无实数根 B.有两个相同的实数根
C.有两个不同的实数根 D.无法判断
12.如图，小树在路灯的照射下形成投影.若树高，树影，树与路灯的水平距离.则路灯的高度为（ ）

A. B. C. D.
13.如图，将直角三角形绕点逆时针旋转一定角度得到直角三角形，若，若，则的度数为（ ）

A. B. C. D.
14.你知道吗？平时我们在跳大绳时，绳甩到最高处的形状可近似地看为抛物线.如图所示，正在甩绳的甲、乙两名学生拿绳的手间距为，距地面均为，学生丙、丁分别站在距甲拿绳的手水平距离、处.绳子在甩到最高处时刚好通过他们的头顶.已知学生丙的身高是，则学生丁的身高为（建立的平面直角坐标系如图所示）（ ）

A. B. C.1.66 D.
15.如图，点是等边三角形的中心，、、分别是、、的中点，则与是位似三角形，此时与的位似比、位似中心分别是（ ）

A.2、点 B.、点 C.2、点 D.、点
16.如图，在宽为，长为的矩形地面上修筑同样宽的道路（图中阴影部分），余下的部分种上草坪.要使草坪的面积为，求道路的宽.如果设小路宽为，根据题意，所列方程正确的是（ ）

A. B.
C. D.
二、填空题（本大题共3个小题，每空3分，共计9分）
17.计算：______.
18.如图，测量河宽（假设河的两岸平行），在点测得，点测得，又，则河宽为______（结果保留根号）.

19.如图是一个几何体的三视图，根据图中所示数据求得个几何体的侧面积是______.（结果保留）

三、解答题（本大题共计66分）
20.（本小题满分10分）适当的方法解方程：
（1）
（2）
21.（本小题满分7分）如图，点，分别在的边，上，且，，，，求证：.

22.（本小题满分8分）如图，在平面直角坐标系中，的三个顶点坐标为，，，绕原点逆时针旋转，得到.向右平移6个单位，再向上平移2个单位得到.
（1）画出和；
（2）是的边上一点，经旋转、平移后点的对应点分别为、，请写出点、的坐标.

23.（本小题满分10分））如图，为的直径，为上一点，与过点的直线互相垂直，垂足为，平分.
（1）求证：为的切线.
（2）若，，求的半径.

24.（本小题满分10分）如图，反比例函数的图象与一次函数的图象相交于点和点.
（1）求反比例函数解析式和点的坐标：
（2）连接，，求的面积；
（3）结合图象，请直接写出使反比例函数值小于一次函数值的自变量的取值范围.

25.（本小题满分12分）
国庆期间电影《我和我的祖国》上映，在全国范围内掀起了观影狂潮.小王一行5人相约观影，由于票源紧张，只好选择3人去影院，余下2人去影院，已知影院的票价比影院的每张便宜5元，5张影票的总价格为310元.
（1）求影院《我和我的祖国》的电影票为多少钱一张；
（2）次日，A影院《我和我的祖国》的票价与前一日保持不变，观影人数为4000人.影院为吸引客源将《我和我的祖国》票价调整为比影院的票价低但不低于50元，结果影院当天的观影人数比影院的观影人数多了，经统计，当日、两个影院《我和我的祖国》的票房总收入为505200元，求的值.
26.（本小题满分12分）如图，在平面直角坐标系中，直线与轴交于点，与轴交于点.抛物线经过，两点，且与轴交于另一点（点在点右侧）.
（1）求抛物线的解析式及点坐标；
（2）若点是线段上一动点，过点的直线平行轴交轴于点，交抛物线于点.求长的最大值；
（3）试探究当取最大值时，在轴下方抛物线上是否存在点，使以，，，为顶点的四边形是平行四边形？若存在，请求出点的坐标；若不存在，试说明理由.



2022-2023年度九年级期末数学答案
一、选择题：（1-10每题2分，11-16每题3分，共42分）
1-5BCDDB 6-10ADCAB 11-16 ADCBDB
二、填空题：（每题3分，共9分）
17. 1 18. 19.
三、解答题：（共69分）
20．（每题5分，共10分）
(1), (2)，
21．证明：∵AC=3，AB=2.5，EC=2，DB=3.5．
∴AE=5，AD=6． （2分）
∴，．
∴． （5分）
∵∠A=∠A，∴△ABC∽△AED．（7分）
22.解：（1）如图所示：△A1B1C1和△A2B2C2，即为所求；（6分）

（2）由题意可得：P1（﹣b，a），P2（﹣b+6，a+2）．（8分）
23、解：（1）如图，连接OC，∵OA＝OC，∴∠OAC＝∠OCA，

∵AC平分∠DAB，∴∠DAC＝∠OAC，∴∠OCA＝∠DAC，
∴AD∥OC，∵AD⊥DC，∴OC⊥DC，
又OC是⊙O的半径，∴DC为⊙O的切线；(5分）
（2）过点O作OE⊥AC于点E，
在Rt△ADC中，AD＝3，DC＝，
∴tan∠DAC＝，∴∠DAC＝30°，∴AC＝2DC＝2，
∵OE⊥AC，
根据垂径定理，得
AE＝EC＝AC＝，∵∠EAO＝∠DAC＝30°，∴OA＝＝2，
∴⊙O的半径为2．（10分）
24.解：把代入，得，∴ ．
∴ 反比例函数的解析式为．（3分）
联立解得或 ∴点的坐标为．（5分）

设直线与轴交于点．
可知点的坐标为，
∴ ．（6分）
∴ ．（8分）
由图像可知，当或时，反比例函数值小于一次函数值．（10分）
25、解：（1）设A影院《我和我的祖国》的电影票为x元一张，由题意得：
3x+2（x+5）＝310……………（2分）
∴3x+2x＝300
∴x＝60 …………………（3分）
答：A影院《我和我的祖国》的电影票为60元一张；…………（4分）
（2）由题意得：
60×4000+60（1﹣a%）×4000（1+2a%）＝505200 ………………（6分）
化简得：2400（1﹣a%）（1+2a%）＝2652
设a%＝t，则方程可化为：2t2﹣t+0.105＝0
解得：t1＝15%，t2＝35%……………………（8分）
∵当t1＝15%时，60×（1﹣15%）＝51＞50；
当t2＝35%时，60×（1﹣35%）＝39＜50，……………（10分）
故t1＝15%符合题意，t2＝35%不符合题意；
∴当t1＝15%时，a＝15．
答：a的值为15．…………………（12分）
26、解：(1) 当y＝0时，
∴A(－1, 0)
当x＝0时， ∴ C(0,－3)
∴∴
抛物线的解析式是： …………（3分）
当y＝0时，
解得： x1＝－1 x2＝3 ∴ B(3, 0) …………（4分）
（2）由（1）知 B(3, 0) ， C(0,－3) 直线BC的解析式是：
设M（x,x-3）(0≤x≤3)，则E（x,x2-2x-3）
∴ME=(x-3)-( x2-2x-3)=-x2+3x =
∴当 时，ME的最大值＝ …………（8分）
（3）答：不存在. …………（9分）
由（2）知 ME 取最大值时ME＝，E，M
∴MF＝，BF=OB-OF=.
设在抛物线x轴下方存在点P，使以P、M、F、B为顶点的四边形是平行四边形，
则BP∥MF，BF∥PM. ∴P1或 P2
当P1时，由（1）知
∴P1不在抛物线上. …………（10分）
当P2时，由（1）知
∴P2不在抛物线上. …………（11分）
综上所述：抛物线x轴下方不存在点P，使以P、M、F、B为顶点的四边形是平行四边形.…………（12分）