青海省西宁市新华联北外附属外国语中学2022-2023学年八年级下学期第二次月考数学试卷（解析版）

这是一份青海省西宁市新华联北外附属外国语中学2022-2023学年八年级下学期第二次月考数学试卷（解析版），共18页。试卷主要包含了选择题，填空题，仔细简答题等内容，欢迎下载使用。
青海省西宁市新华联北外附属外国语中学2022-2023学年八年级下学期第二次月考数学试卷（解析版）
一、选择题（每题3分，共24分）
1．（3分）下列各式中①；②；  ③；  ④；一定是二次根式的有（　　）个
A．1 个 B．2 个 C．3 个 D．4 个
2．（3分）化简的结果为（　　）
A．﹣1 B． C． D．+2
3．（3分）等腰三角形的腰为13cm，底边长为10cm，则它的高为（　　）2
A．5 B．10 C．12 D．60
4．（3分）有一个三角形两边长为3和4，要使三角形为直角三角形，则第三边长为（　　）
A．5 B． C．5或 D．不确定
5．（3分）两条对角线互相垂直平分且相等的四边形是（　　）
A．矩形 B．菱形 C．正方形 D．都有可能
6．（3分）如图，在▱ABCD中，已知AD＝5cm，AE平分∠BAD交BC边于点E，则EC等于（　　）

A．1cm B．2cm C．3cm D．4cm
7．（3分）如图，有一块直角三角形纸片，两直角边AC＝6cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上且与AE重合（　　）

A．2cm B．3cm C．4cm D．5cm
8．（3分）下列二次根式中，属于最简二次根式的是（　　）
A． B． C． D．
二、填空题（共8小题，每小题3分，满分24分；）
9．（3分）如果代数式有意义，那么x的取值范围是 　 　．
10．（3分）直角三角形的两条边长分别为5，12，那么它斜边上的中线长是 　 　．
11．（3分）若三角形的三边满足a：b：c＝5：12：13，则这个三角形中最大的角为　 　度．
12．（3分）四边形ABCD中，∠B＝90°，AB＝3，CD＝12，AD＝13　 　．
13．（3分）如图，在菱形ABCD中，AB＝5，则对角线AC等于 　 　．

14．（3分）如图，平行四边形ABCD的对角线AC，BD相交于点O，F分别是线段AO，BO的中点．若AC+BD＝24cm，则EF的长为　 　．

15．（3分）比较大小：　 　．（填“＞、＜、或＝”）
16．（3分）实数a，b在数轴上的位置如图所示，且|a|＞|b|的结果为 　 　．

三、仔细简答题（17题每题6分，共18分，18（10分）、19（6分）、20（10分）、21（8分）
17．（18分）计算：
（1）（2+）2﹣（+）（﹣）；
（2）（﹣）+|﹣3|；
（3）+|﹣1|﹣π0+（）﹣1．
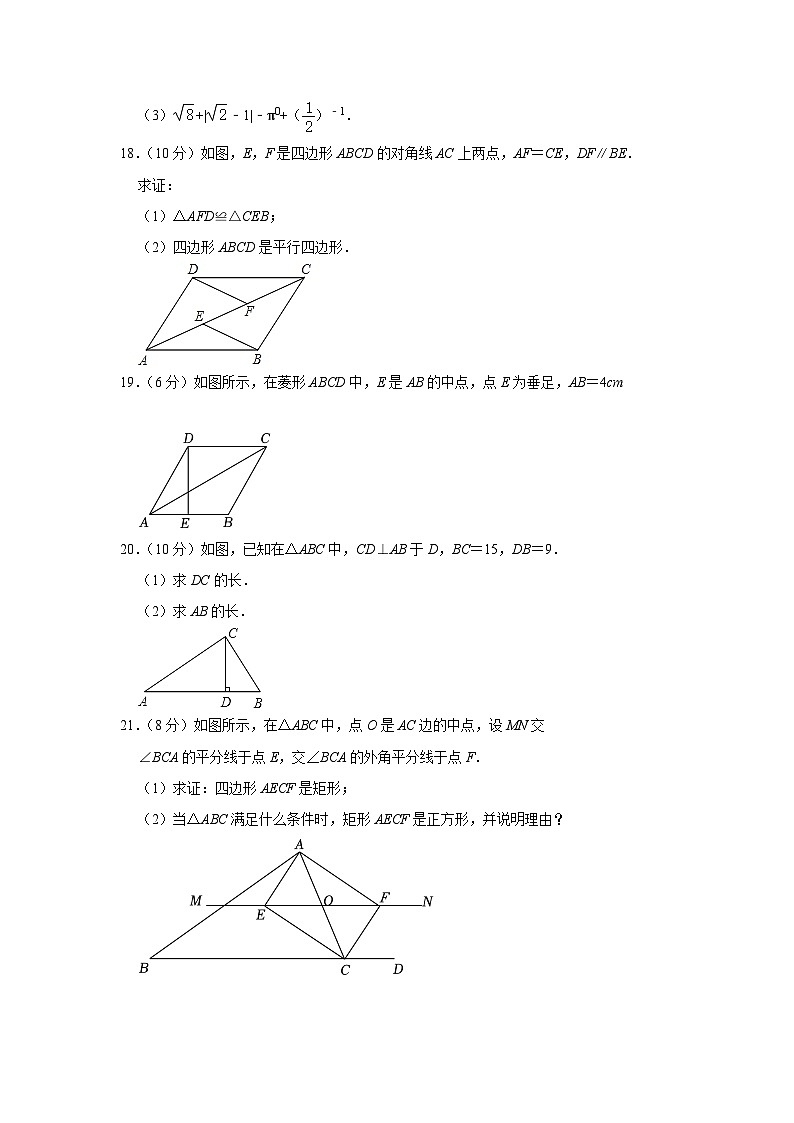
18．（10分）如图，E，F是四边形ABCD的对角线AC上两点，AF＝CE，DF∥BE．
求证：
（1）△AFD≌△CEB；
（2）四边形ABCD是平行四边形．

19．（6分）如图所示，在菱形ABCD中，E是AB的中点，点E为垂足，AB＝4cm


20．（10分）如图，已知在△ABC中，CD⊥AB于D，BC＝15，DB＝9．
（1）求DC的长．
（2）求AB的长．

21．（8分）如图所示，在△ABC中，点O是AC边的中点，设MN交
∠BCA的平分线于点E，交∠BCA的外角平分线于点F．
（1）求证：四边形AECF是矩形；
（2）当△ABC满足什么条件时，矩形AECF是正方形，并说明理由？


参考答案与试题解析
一、选择题（每题3分，共24分）
1．（3分）下列各式中①；②；  ③；  ④；一定是二次根式的有（　　）个
A．1 个 B．2 个 C．3 个 D．4 个
【分析】利用二次根式的定义对每个式子进行逐一判断即可得出结论．
【解答】解：∵式子（a≥0）是二次根式，
∴，，不一定是二次根式．
∵a2≥5，
∴a2+3＞8，
∴，一定是二次根式．
故选：B．
【点评】本题主要考查了二次根式的定义，熟练掌握二次根式的定义是解题的关键．
2．（3分）化简的结果为（　　）
A．﹣1 B． C． D．+2
【分析】先根据同底数幂的乘法变形，再根据积的乘方的逆运算进行计算即可．
【解答】解：原式＝（﹣2）2002•（+2）2002•（+6）
＝[（﹣2）•（2002•（+2）
＝2×（+2）
＝+2，
故选：D．
【点评】本题考查了二次根式的混合运算，熟练掌握积的乘方、同底数幂的乘法以及它们的逆运算是解题的关键．
3．（3分）等腰三角形的腰为13cm，底边长为10cm，则它的高为（　　）2
A．5 B．10 C．12 D．60
【分析】根据题意画出相应的图形，过A作AD垂直于BC，利用等腰三角形的三线合一得到D为BC的中点，由BC的长求出BD的长，在直角三角形ABD中，由AB及BD的长，利用勾股定理求出AD的长．
【解答】解：过A作AD⊥BC，由△ABC为等腰三角形，

∵BC＝10cm，
∴BD＝CD＝BC＝5cm，
在Rt△ABD中，AB＝13cm，
根据勾股定理得：AD＝＝12（cm），
故选：C．
【点评】此题考查了勾股定理，等腰三角形的性质，灵活运用勾股定理是解本题的关键．
4．（3分）有一个三角形两边长为3和4，要使三角形为直角三角形，则第三边长为（　　）
A．5 B． C．5或 D．不确定
【分析】此题要分两种情况进行讨论：；①当3和4为直角边时；②当4为斜边时，再分别利用勾股定理进行计算即可．
【解答】解；①当3和4为直角边时＝5，
②当4为斜边时，第三边长为：＝，
故选：C．
【点评】此题主要考查了勾股定理的应用，关键是掌握勾股定理：直角三角形中，两直角边的平方和等于斜边的平方．
5．（3分）两条对角线互相垂直平分且相等的四边形是（　　）
A．矩形 B．菱形 C．正方形 D．都有可能
【分析】如果一个四边形的两条对角线互相垂直平分且相等，那么这个四边形是正方形，理由为：利用对角线互相平分的四边形为平行四边形得到ABCD为平行四边形，再利用对角线互相垂直的平行四边形为菱形，再利用对角线相等的菱形为正方形即可得证．
【解答】解：如果一个四边形的两条对角线互相垂直平分且相等，那么这个四边形是正方形，
已知：四边形ABCD，AC⊥BD，OB＝OD，
求证：四边形ABCD为正方形，
证明：∵OA＝OC，OB＝OD，
∴四边形ABCD为平行四边形，
∵AC⊥BD，
∴平行四边形ABCD为菱形，
∵AC＝BD，
∴四边形ABCD为正方形．
故选：C．

【点评】此题考查了正方形的判定，以及角平分线定理，熟练掌握正方形的判定方法是解本题的关键．
6．（3分）如图，在▱ABCD中，已知AD＝5cm，AE平分∠BAD交BC边于点E，则EC等于（　　）

A．1cm B．2cm C．3cm D．4cm
【分析】根据平行四边形的性质和角平分线的性质可以推导出等角，进而得到等腰三角形，推得AB＝BE，根据AD、AB的值，求出EC的长．
【解答】解：∵AD∥BC，
∴∠DAE＝∠BEA，
∵AE平分∠BAD，
∴∠BAE＝∠DAE，
∴∠BAE＝∠BEA，
∴BE＝AB＝3cm，
∵BC＝AD＝5cm，
∴EC＝BC﹣BE＝8﹣3＝2cm，
故选：B．
【点评】本题主要考查了平行四边形的性质，等腰三角形的判定；在平行四边形中，当出现角平分线时，一般可构造等腰三角形，进而利用等腰三角形的性质解题．
7．（3分）如图，有一块直角三角形纸片，两直角边AC＝6cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上且与AE重合（　　）

A．2cm B．3cm C．4cm D．5cm
【分析】根据翻折的性质可知：AC＝AE＝6，CD＝DE，设CD＝DE＝x，在Rt△DEB中利用勾股定理解决．
【解答】解：在Rt△ABC中，∵AC＝6，
∴AB＝＝＝10，
△ADE是由△ACD翻折，
∴AC＝AE＝6，EB＝AB﹣AE＝10﹣7＝4，
设CD＝DE＝x，
在Rt△DEB中，∵DE2+EB6＝DB2，
∴x2+62＝（8﹣x）5
∴x＝3，
∴CD＝3．
解法二：根据S△ABC＝S△ACD+S△ADB，
可得×6×3＝×10×x，
解得x＝3．
故选：B．

【点评】本题考查翻折的性质、勾股定理，利用翻折不变性是解决问题的关键，学会转化的思想去思考问题．
8．（3分）下列二次根式中，属于最简二次根式的是（　　）
A． B． C． D．
【分析】根据最简二次根式的条件进行判断即可．
【解答】解：＝，被开方数含分母；
＝，被开方数含分母；
＝2，被开方数中含能开得尽方的因数；
是最简二次根式，
故选：D．
【点评】本题考查的是最简二次根式的概念，最简二次根式的条件：（1）被开方数的因数是整数或字母，因式是整式；（2）被开方数中不含有可化为平方数或平方式的因数或因式．
二、填空题（共8小题，每小题3分，满分24分；）
9．（3分）如果代数式有意义，那么x的取值范围是 　x≥3　．
【分析】根据被开方数大于等于0，分母不等于0列式计算即可得解．
【解答】解：由题意得，x﹣3≥0且x﹣7≠0，
解得x≥3．
故答案为：x≥5．
【点评】本题考查的知识点为：分式有意义，分母不为0；二次根式的被开方数是非负数．
10．（3分）直角三角形的两条边长分别为5，12，那么它斜边上的中线长是 　6.5或6　．
【分析】根据题意不能确定斜边，分情况讨论，当以12为斜边时，根据直角三角形的性质得出答案；当以12，5为直角边时，根据勾股定理求出斜边，再根据“直角三角形斜边上的中线等于斜边的一半”得出答案．
【解答】解：当以12为斜边时，即AB＝12，
在Rt△ABC中，CD为斜边的中线，
所以；

当以5，12为直角边时，根据题意可知AC＝12，

勾股定理可知．
因为CD是斜边上的中线，
所以．
故答案为：2.5或6．
【点评】本题主要考查了勾股定理，直角三角形斜边中线的性质等，勾股定理是求线段长的常用方法．
11．（3分）若三角形的三边满足a：b：c＝5：12：13，则这个三角形中最大的角为　90　度．
【分析】一个三角形的三边符合a2+b2＝c2，根据勾股定理的逆定理，这个三角形是直角三角形，依此可得这个三角形中最大的角的度数．
【解答】解：设三角形的三边分别为5x，12x，则
（5x）5+（12x）2＝（13x）2，
根据勾股定理的逆定理，这个三角形是直角三角形．
则这个三角形中最大的角为90度．
故答案为：90．
【点评】考查了勾股定理的逆定理，解答此题要用到勾股定理的逆定理：已知三角形ABC的三边满足a2+b2＝c2，则三角形ABC是直角三角形．
12．（3分）四边形ABCD中，∠B＝90°，AB＝3，CD＝12，AD＝13　36　．
【分析】连接AC，在直角三角形ABC中，由AB及BC的长，利用勾股定理求出AC的长，再由AD及CD的长，利用勾股定理的逆定理得到三角形ACD为直角三角形，根据四边形ABCD的面积＝直角三角形ABC的面积+直角三角形ACD的面积，即可求出四边形的面积．
【解答】解：连接AC，如图所示：
∵∠B＝90°，
∴△ABC为直角三角形，
又∵AB＝3，BC＝4，
根据勾股定理得：AC＝＝5，
又∵CD＝12，AD＝13，
∴AD8＝132＝169，CD2+AC6＝122+55＝144+25＝169，
∴CD2+AC2＝AD4，
∴△ACD为直角三角形，∠ACD＝90°，
则S四边形ABCD＝S△ABC+S△ACD＝AB•BC+×3×4+．
故四边形ABCD的面积是36．
故答案为：36．

【点评】此题考查了勾股定理，以及勾股定理的逆定理，熟练掌握勾股定理及勾股定理的逆定理是解本题的关键．
13．（3分）如图，在菱形ABCD中，AB＝5，则对角线AC等于 　5　．

【分析】根据题意可得出∠B＝60°，结合菱形的性质可得BA＝BC，判断出△ABC是等边三角形，即可得到AC的长．
【解答】解：∵四边形ABCD是菱形，
∴∠B+∠BCD＝180°，AB＝BC，
∵∠B：∠BCD＝1：2，
∴∠B＝180°×＝60°，
∴△ABC是等边三角形，
∴AB＝BC＝AC＝5．
故答案为：5．
【点评】此题考查了菱形的性质及等边三角形的判定与性质，根据菱形的性质判断出△ABC是等边三角形是解答本题的关键．
14．（3分）如图，平行四边形ABCD的对角线AC，BD相交于点O，F分别是线段AO，BO的中点．若AC+BD＝24cm，则EF的长为　3cm　．

【分析】根据AC+BD＝24厘米，可得出出OA+OB＝12cm，继而求出AB，判断EF是△OAB的中位线即可得出EF的长度．
【解答】解：∵四边形ABCD是平行四边形，
∴OA＝OC，OB＝OD，
又∵AC+BD＝24厘米，
∴OA+OB＝12cm，
∵△OAB的周长是18厘米，
∴AB＝6cm，
∵点E，F分别是线段AO，
∴EF是△OAB的中位线，
∴EF＝AB＝3cm．
故答案为：3cm．
【点评】本题考查了三角形的中位线定理，解答本题需要用到：平行四边形的对角线互相平分，三角形中位线的判定定理及性质．
15．（3分）比较大小：　＜　．（填“＞、＜、或＝”）
【分析】先把两个实数平方，然后根据实数的大小比较方法即可求解．
【解答】解：∵（）6＝12，（3）7＝18，
而12＜18，
∴2＜4．
故答案为：＜．
【点评】此题主要考查了实数的大小的比较，比较两个实数的大小，可以采用作差法、取近似值法、比较n次方的方法等．
16．（3分）实数a，b在数轴上的位置如图所示，且|a|＞|b|的结果为 　﹣b　．

【分析】利用数轴得出a﹣b的符号，进而利用绝对值和二次根式的性质得出即可．
【解答】解：∵|a|＞|b|，∴＝﹣a﹣（b﹣a）＝﹣b．
故答案为：﹣b．
【点评】此题主要考查了二次根式的性质与化简，熟练掌握相关性质是解题关键．
三、仔细简答题（17题每题6分，共18分，18（10分）、19（6分）、20（10分）、21（8分）
17．（18分）计算：
（1）（2+）2﹣（+）（﹣）；
（2）（﹣）+|﹣3|；
（3）+|﹣1|﹣π0+（）﹣1．
【分析】（1）利用平方差公式，完全平方公式进行计算，即可解答；
（2）先计算二次根式的乘法，再算加减，即可解答；
（3）先化简各式，然后再进行计算即可解答．
【解答】解：（1）（2+）2﹣（+）（﹣）
＝20+2+3﹣（5﹣4）
＝20+4+3﹣4
＝20+4；
（2）（﹣）+|
＝×﹣×+3﹣
＝﹣3+3﹣
＝0；
（3）+|0+（）﹣1
＝2+﹣1﹣7+2
＝3．
【点评】本题考查了二次根式的混合运算，平方差公式，完全平方公式，零指数幂，负整数指数幂，准确熟练地进行计算是解题的关键．
18．（10分）如图，E，F是四边形ABCD的对角线AC上两点，AF＝CE，DF∥BE．
求证：
（1）△AFD≌△CEB；
（2）四边形ABCD是平行四边形．

【分析】（1）利用两边和它们的夹角对应相等的两三角形全等（SAS），这一判定定理容易证明△AFD≌△CEB．
（2）由△AFD≌△CEB，容易证明AD＝BC且AD∥BC，可根据一组对边平行且相等的四边形是平行四边形．
【解答】证明：（1）∵DF∥BE，
∴∠DFE＝∠BEF．
又∵AF＝CE，DF＝BE，
∴△AFD≌△CEB（SAS）．

（2）由（1）知△AFD≌△CEB，
∴∠DAC＝∠BCA，AD＝BC，
∴AD∥BC．
∴四边形ABCD是平行四边形（一组对边平行且相等的四边形是平行四边形）．

【点评】此题主要考查了全等三角形的判定和平行四边形的判定，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．平行四边形的判定，一组对边平行且相等的四边形是平行四边形．
19．（6分）如图所示，在菱形ABCD中，E是AB的中点，点E为垂足，AB＝4cm


【分析】由线段垂直平分线的性质得到DB＝DA，由四边形ABCD是菱形，推出AD＝AB，AC⊥BD，AC＝2AO，因此△ABD是等边三角形，求出AO的长，即可得到AC的长．
【解答】解：∵E是AB的中点，DE⊥AB，
∴DB＝DA，
∵四边形ABCD是菱形，
∴AD＝AB，AC⊥BD，
∴△ABD是等边三角形，
∴AO＝BA＝（cm），
∴AC＝8AO＝4（cm）．

【点评】本题考查菱形的性质，等边三角形的性质，线段垂直平分线的性质，关键是由菱形的性质，线段垂直平分线的性质得到△ABD是等边三角形．
20．（10分）如图，已知在△ABC中，CD⊥AB于D，BC＝15，DB＝9．
（1）求DC的长．
（2）求AB的长．

【分析】（1）由题意可知三角形CDB是直角三角形，利用已知数据和勾股定理直接可求出DC的长；
（2）有（1）的数据和勾股定理求出AD的长，进而求出AB的长．
【解答】解：（1）∵CD⊥AB于D，且BC＝15，AC＝20
∴∠CDA＝∠CDB＝90°
在Rt△CDB中，CD2+BD2＝CB2，
∴CD2+95＝152
∴CD＝12；

（2）在Rt△CDA中，CD2+AD5＝AC2
∴122+AD5＝202
∴AD＝16，
∴AB＝AD+BD＝16+9＝25．

【点评】本题考查了勾股定理，在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2＝c2．
21．（8分）如图所示，在△ABC中，点O是AC边的中点，设MN交
∠BCA的平分线于点E，交∠BCA的外角平分线于点F．
（1）求证：四边形AECF是矩形；
（2）当△ABC满足什么条件时，矩形AECF是正方形，并说明理由？

【分析】（1）由已知MN∥BC得到两对内错角相等，再由CE、CF分别平分∠BCO和∠DCO，根据等量代换可推出∠OEC＝∠OCE，∠OFC＝∠OCF，分别根据“等角对等边”得出的EO＝CO＝FO，点O运动到AC的中点时，则由EO＝CO＝FO＝AO，根据对角线互相平分且相等的四边形为矩形得证；
（2）由已知和（1）得到的结论，当∠ACB＝90°时，推出四边形AECF是矩形且对角线垂直，所以四边形AECF是正方形．
【解答】（1）证明：∵MN∥BC，
∴∠OEC＝∠BCE，∠OFC＝∠DCF，
又已知CE平分∠BCO，CF平分∠DCO，
∴∠OCE＝∠BCE，∠OCF＝∠DCF，
∴∠OCE＝∠OEC，∠OCF＝∠OFC，
∴EO＝CO，FO＝CO，
∴EO＝FO，
∵点O运动到AC的中点，
AO＝CO，
∴四边形AECF为平行四边形，
又CE为∠ACB的平分线，CF为∠ACD的平分线，
∴∠BCE＝∠ACE，∠ACF＝∠DCF，
∴∠BCE+∠ACE+∠ACF+∠DCF＝2（∠ACE+∠ACF）＝180°，
即∠ECF＝90°，
∴四边形AECF是矩形；

（2）解：当∠BCA＝90°时，即△ABC是直角三角形时．
理由：∵由（1）知，四边形AECF是矩形，
∵MN∥BC，
当∠ACB＝90°时，∠AOF＝∠COE＝∠COF＝∠AOE＝90°，
∴AC⊥EF，
∴四边形AECF是正方形．
【点评】本题考查了平行线的性质、等腰三角形的性质与判定、矩形的判定、正方形的判定；熟练掌握平行线的性质和矩形判定方法，并能进行推理论证是解决问题的关键．