四川省成都市石室中学2023届高三高考模拟测试数学（理科）试题（含解析）

这是一份四川省成都市石室中学2023届高三高考模拟测试数学（理科）试题（含解析），共25页。试卷主要包含了单选题，填空题，双空题，解答题等内容，欢迎下载使用。

四川省成都市石室中学2023届高三高考模拟测试数学（理科）试题
学校:___________姓名：___________班级：___________考号：___________

一、单选题
1．已知集合，若Ü，则实数（    ）
A．或1 B．0或1 C．1 D．
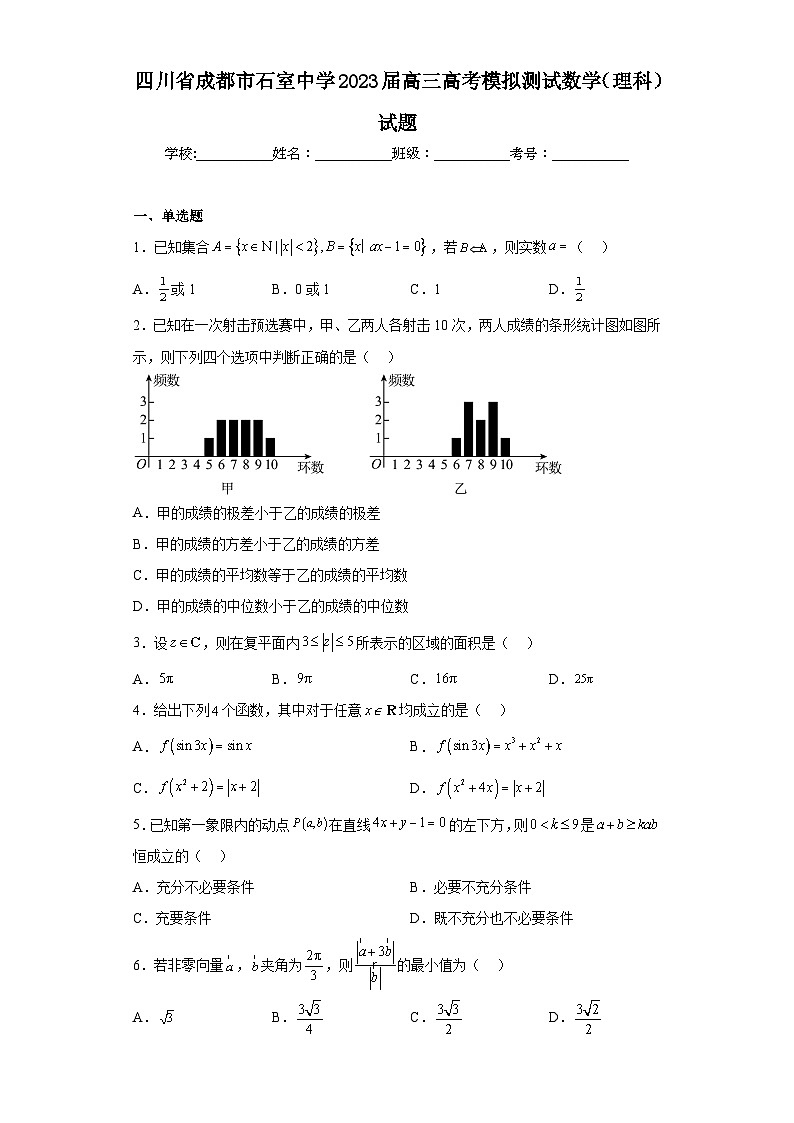
2．已知在一次射击预选赛中，甲、乙两人各射击10次，两人成绩的条形统计图如图所示，则下列四个选项中判断正确的是（    ）
  
A．甲的成绩的极差小于乙的成绩的极差
B．甲的成绩的方差小于乙的成绩的方差
C．甲的成绩的平均数等于乙的成绩的平均数
D．甲的成绩的中位数小于乙的成绩的中位数
3．设，则在复平面内所表示的区域的面积是（    ）
A． B． C． D．
4．给出下列个函数，其中对于任意均成立的是（    ）
A． B．
C． D．
5．已知第一象限内的动点在直线的左下方，则是恒成立的（    ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
6．若非零向量，夹角为，则的最小值为（    ）
A． B． C． D．
7．在数列中,若,则（    ）
A． B．
C． D．
8．若过原点与曲线相切的直线，切点均与原点不重合的有2条，则的取值范围是（    ）
A． B． C． D．
9．已知函数，若方程在上恰有5个不同实根，则m的取值范围是（    ）
A． B． C． D．
10．分形的数学之美，是以简单的基本图形，凝聚扩散，重复累加，以迭代的方式而形成的美丽的图案．自然界中存在着许多令人震撼的天然分形图案，如鹦鹉螺的壳、蕨类植物的叶子、孔雀的羽毛、菠萝等．如图所示，为正方形经过多次自相似迭代形成的分形图形，且相邻的两个正方形的对应边所成的角为．若从外往里最大的正方形边长为9，则第5个正方形的边长为（    ）

A． B． C．4 D．
11．如图，在棱长为的正方体中，分别为棱的中点，为线段上一个动点，则下列说法不正确的是（    ）
  
A．存在点，使直线平面
B．存在点，使平面平面
C．三棱锥的体积为定值
D．平面截正方体所得截面的最大面积为
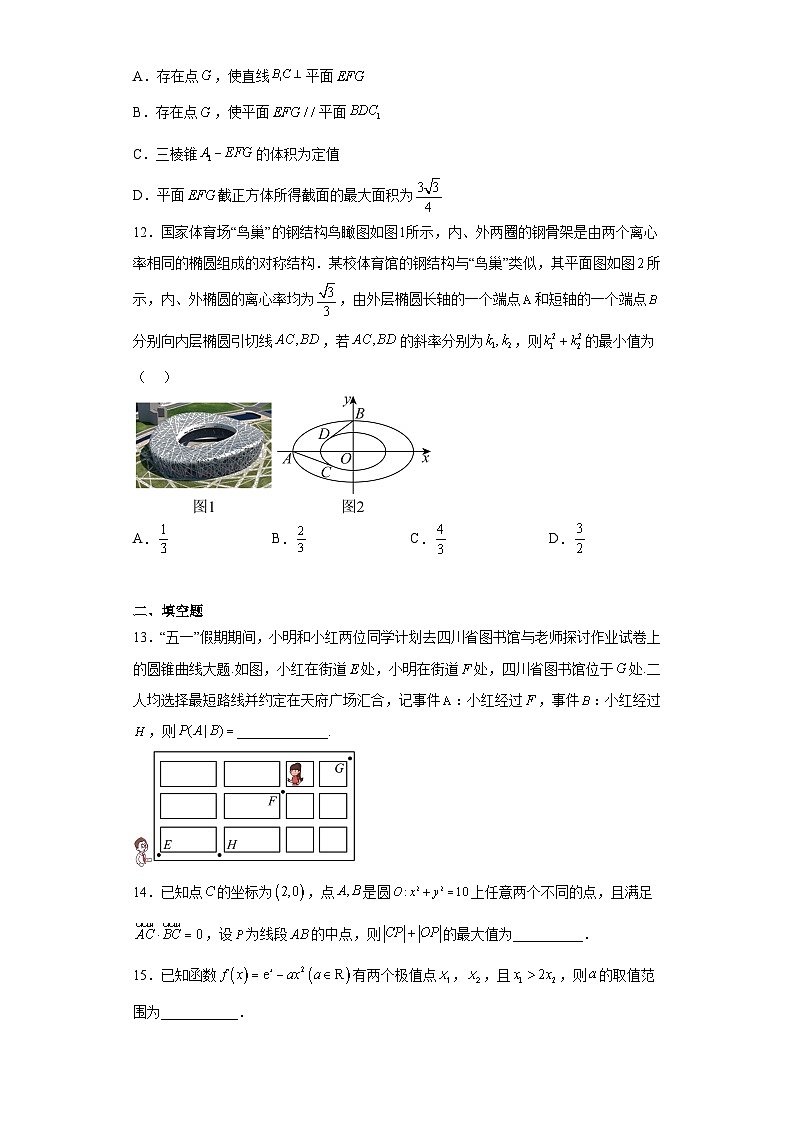
12．国家体育场“鸟巢”的钢结构鸟瞰图如图所示，内、外两圈的钢骨架是由两个离心率相同的椭圆组成的对称结构．某校体育馆的钢结构与“鸟巢”类似，其平面图如图所示，内、外椭圆的离心率均为，由外层椭圆长轴的一个端点和短轴的一个端点分别向内层椭圆引切线，若的斜率分别为，则的最小值为（    ）

A． B． C． D．

二、填空题
13．“五一”假期期间，小明和小红两位同学计划去四川省图书馆与老师探讨作业试卷上的圆锥曲线大题.如图，小红在街道处，小明在街道处，四川省图书馆位于处.二人均选择最短路线并约定在天府广场汇合，记事件：小红经过，事件：小红经过，则_____________.
  
14．已知点的坐标为，点是圆上任意两个不同的点，且满足，设为线段的中点，则的最大值为__________．
15．已知函数有两个极值点，，且，则的取值范围为___________．

三、双空题
16．定义：对于各项均为整数的数列，如果(=1，2，3，…)为完全平方数，则称数列具有“性质”；不论数列是否具有“性质”，如果存在数列与不是同一数列，且满足下面两个条件：
（1）是的一个排列；
（2）数列具有“性质”，则称数列具有“变换性质”.给出下面三个数列：
①数列的前项和；
②数列：1，2，3，4，5；
③数列：1，2，3，4，5，6.
具有“性质”的为________；具有“变换性质”的为_________.

四、解答题
17．如图，在中，，点在延长线上，且．

(1)求；
(2)若面积为，求．
18．5G技术对社会和国家十分重要．从战略地位来看，业界一般将其定义为继蒸汽机革命、电气革命和计算机革命后的第四次工业革命．某科技集团生产A，B两种5G通信基站核心部件，下表统计了该科技集团近几年来在A部件上的研发投入（亿元）与收益y（亿元）的数据，结果如下：
研发投入x（亿元）
1
2
3
4
5
收益y（亿元）
3
7
9
10
11
(1)利用样本相关系数r说明是否可以用线性回归模型拟合y与x的关系（当时，可以认为两个变量有很强的线性相关性）；
(2)求出y关于x的经验回归方程，并利用该方程回答下列问题：
①若要使生产A部件的收益不低于15亿元，估计至少需要投入多少研发资金？（精确到0.001亿元）
②该科技集团计划用10亿元对A，B两种部件进行投资，对B部件投资元所获得的收益y近似满足，则该科技集团针对A，B两种部件各应投入多少研发资金，能使所获得的总收益P最大．
附：样本相关系数，
回归直线方程的斜率，截距．
19．如图，在三棱锥中，底面，.点、、分别为棱、、的中点，是线段的中点，，.

(1)求证：平面；
(2)已知点在棱上，且直线与直线所成角的余弦值为，求线段的长．
20．已知椭圆，圆与轴的交点恰为的焦点，且上的点到焦点距离的最大值为.
(1)求的标准方程；
(2)不过原点的动直线与交于两点，平面上一点满足，连接交于点（点在线段上且不与端点重合），若，试判断直线与圆的位置关系，并说明理由.
21．已知函数
(1)若单调递增，求a的值；
(2)判断（且）与的大小，并说明理由.
22．在平面直角坐标系xOy中，曲线的参数方程为，（t为参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.
(1)求的普通方程及的直角坐标方程；
(2)若曲线，没有公共点，求a的取值范围.
23．已知函数的最大值为2．
(1)求的值；
(2)证明：．

参考答案：
1．B
【分析】先求得合，再分和，两种情况讨论，结合题意，即可求解.
【详解】解：由集合，
对于方程，
当时，此时方程无解，可得集合，满足Ü；
当时，解得，要使得Ü，则满足，可得，
所以实数的值为或.
故选：B.
2．D
【分析】根据条形统计图可分别计算出甲、乙的平均数、中位数、极差，从而判断出ACD的正误；根据成绩的分散程度可判断B的正误.
【详解】对于A，甲的成绩的极差为，乙的成绩的极差为，
甲的成绩的极差大于乙的成绩的极差，故A错误．
对于B，由条形统计图得甲的成绩相对分散，乙的成绩相对稳定，
甲的成绩的方差大于乙的成绩的方差，故B错误；
对于C，甲的成绩的平均数为，
乙的成绩的平均数为，
甲的成绩的平均数小于乙的成绩的平均数，故C错误；
对于D，甲的成绩的中位数为；乙的成绩的中位数为：，
甲的成绩的中位数小于乙的成绩的中位数，故D正确；
故选：D
3．C
【分析】在复平面内作出满足的复数对应的点的轨迹，可知所求区域为圆环，确定两圆的半径，结合圆的面积公式可求得结果.
【详解】满足条件的复数在复平面内对应的点的轨迹是以原点为圆心，半径为的圆，
满足条件的复数在复平面内对应的点的轨迹是以原点为圆心，半径为的圆，
则在复平面内所表示的区域为圆环，如下图中阴影部分区域所示：

所以，在复平面内所表示的区域的面积是.
故选：C.
4．D
【分析】根据函数定义逐项判断ABC，采用换元的方法求解D中函数的解析式并进行判断.
【详解】对于A，当时，；当时，，与函数定义矛盾，不符合；
对于B，当时，；当时，，与函数定义矛盾，不符合；
对于C，当时，；当时，，与函数定义矛盾，不符合；
对于D，令，则，所以，
令，所以，
所以，
所以，符合.
故选：D.
5．A
【分析】依题意可得、且，若恒成立，即恒成立，利用基本不等式求出，即可求出的取值范围，再根据充分条件、必要条件的定义判断即可.
【详解】因为第一象限内的动点在直线的左下方，
所以、且，
若恒成立，即恒成立，
因为，
当且仅当时取等号，所以，
所以是恒成立的充分不必要条件.
故选：A
6．C
【分析】首先根据向量数量积的定义有，根据向量数量的运算律结合二次函数的性质即可得到的最值.
【详解】由向量夹角为,得,
所以
,
当时取等号.所以的最小值为,
故选：C.
7．C
【分析】将转化为,再根据等比数列求和公式求解即可.
【详解】因为
,
所以.
故选:C.
8．C
【分析】求出函数的导函数，设过原点的切线与曲线在处相切，根据导数的几何意义得到方程，整理得，设，利用导数说明函数的单调性，即可求出函数的最值，即可求出参数的取值范围.
【详解】因为，所以，
设过原点的切线与曲线在处相切，
所以切线的斜率，整理得，
设，则，所以当时，当时，
所以在上单调递增，在上单调递减，
所以，且当时，当时，
所以当时过原点与曲线相切的直线有2条.
故选：C
9．D
【分析】求出方程的根，然后根据方程在上恰有5个不同实根列出不等关系，进而求解.
【详解】因为函数，
当时，方程可化为，解得
，则当时，，
当时，方程可化为，解得，
则当时，
因为根据方程在上恰有5个不同实根，
所以这5个不同实根为，则，
故选：D.
10．C
【分析】设第n个正方形的边长为，根据分形特点可得{}是以9为首项，为公比的等比数列，从而可得第5个正方形的边长.
【详解】设第n个正方形的边长为，则由已知可得
∴，
∴{}是以9为首项，为公比的等比数列，
∴.
故选：C．
11．B
【分析】对于A项，可以通过取的中点H、I，连接HI交于G点，判定即可；对于B项，通过反证，利用面与面和面的交线PG、DH是否能平行来判定；对于C项，通过等体积法转化即可判定；对于D项，讨论截面的形状并计算各交线长来判定即可
【详解】对于A项，如图所示，取的中点H、I，连接HI交于G点，
此时，由正方体的性质可得，，
平面，所以平面，故A正确；
  
对于B项，如图所示，连接，为侧面的中心，
则面与面和面分别交于线PG、DH，
若存在G点使平面平面，则，又，
则四边形为平行四边形，即，而，
此时应在延长线上，故B错误；
对于C项，随着G移动但G到面的距离始终不变即，
故是定值，即C正确；
  
对于D项，若点靠C远，如图一所示，过G作，即截面为四边形，
当截面在正方体底面上的投影面积越大，其面积就越大，如下图，
  
显然当在底面的投影为点时，截面为四边形面积最大，
此时为侧面的中心，最大值为，
  
若靠C近时（图二），G作，延长交、延长线于M、H，
连接MK、交，于，则截面为六边形，
当截面在正方体底面上的投影面积越大，其面积就越大，
如下图，六边形在正方体底面的投影为六边形，
设
所以，
当时，取得最大值.
  
设
则当在底面的投影为点时，截面为四边形面积最大，
当为中点时取得最大值，最大值为，，D正确.
故选：B.
12．C
【分析】将直线方程分别与内层椭圆方程联立，由可分别表示出，由基本不等式可求得的最小值.
【详解】设外层椭圆方程为，则内层椭圆方程为，设的方程为，
由得：，
由得：；
设的方程为，
由得：，
由得：．
离心率，，
（当且仅当，即时取等号），
的最小值为.
故选：C.
【点睛】关键点点睛：本题考查直线与椭圆中的最值问题的求解，解题关键是能够根据直线与椭圆相切的位置关系，利用表示出，结合基本不等式确定最小值.
13．/
【分析】根据古典概型概率公式求出和，再根据条件概率公式可求出.
【详解】小红从到的最短路径条数为：，
小红从经过到的最短路径条数为：，故，
小红经过和到的最短路径条数为：，故，
所以.
故答案为：.
14．
【分析】由题意可得，再由基本不等式，带入求解即可得出答案.
【详解】如图，连接，
因为，所以，

因为为线段的中点，所以，
由垂径定理可得，则，
所以，所以的最大值为.
当且仅当时取等.
故答案为：.
15．
【分析】将极值点问题转化为导函数的零点问题，再将零点问题转化为方程的解的问题，构造函数求解即可.
【详解】∵，∴，
∵函数有两个极值点，，
∴，又∵，∴，，
∴，是，即的两个不相等的实数根.
令，则．
①当时，，在区间单调递减，且，
②当时，，在区间单调递减，且，
③当时，，在区间单调递增，且，
∴在处取得极小值，的图象大致如下，

∴若有两个不相等的实数根，，则，即，且，，
令，则，且∵，∴，
又∵，∴，∴，
两边同时取对数，得，∴，
下面求的取值范围，设，则，
令，则，
当时，，∴在上单调递减，
∴当时，，
∴当时，，在上单调递减，
∴，即.
又∵在区间上单调递减，，，
∴，即.
∴实数的取值范围为．
【点睛】易错点睛：本题容易仅当作有两个极值点求得的取值范围，而造成错解，需要再根据，结合所构造函数，转换成的范围，利用的范围再次求解.
16． ① ②
【分析】根据“性质”，“变换性质”的定义逐项判断即可得.
【详解】解：对于①，当时，
，
，2，3，为完全平方数
数列具有“性质”；
对于②，数列1，2，3，4，5，具有“变换性质”，数列为3，2，1，5，4，具有“性质”， 数列具有“变换性质”；
对于③，，1都只有与3的和才能构成完全平方数，，2，3，4，5，6，不具有“变换性质”．
故答案为：①；②．
17．(1)
(2)

【分析】（1）设，利用余弦定理求得，再在和中两次利用正弦定理即可求出比值.
（2）利用三角形面积公式即可求出（1）问的值，再利用余弦定理即可.
【详解】（1）因为,设,则,
由余弦定理得，因为，
所以
在中,由正弦定理得,
在中,由正弦定理得,
因为,所以
整理得.
（2）由得,
由（1）得,所以,
在中,,
由余弦定理得

.
18．(1)答案见解析
(2)回归方程为，①6.684亿元；②在A，B两种部件上分别投入8亿元，2亿元.

【分析】（1）先计算出，再根据公式计算出，再由即可判断；
（2）根据公式先求出回归直线方程，①令，解不等式即可求解；②根据题意，写出总收益的函数表达式，对函数求导，得出函数的单调性，然后利用函数的单调性求出最值即可.
【详解】（1），，
，，，
∴．
可以用线性回归模型拟合y与x的关系．
（2）∵，
∴，
∴y关于的经验回归方程为，
①令，得，解得，
∴若要使生产A部件的收益不低于15亿元，估计至少需要投入6.684亿元研发资金．
②设B部件的研发投入为亿元，则A部件的研发投入为亿元，
总收益，
，
令得，
当时，，P单调递增；当，，P单调递减，
所以当时，P取得最大值22亿元．
所以该科技集团在A，B两种部件上分别投入8亿元，2亿元的研发资金，可使所获得的总收益P最大．
19．(1)证明见解析
(2)或

【分析】（1）以点为原点，以、、所在直线分别为、、轴建立空间直角坐标系，利用空间向量法可证得平面；
（2）设，则，利用空间向量法可得出关于的方程，解出的值，即可得出结论.
【详解】（1）证明：因为底面，，
如图，以点为原点，以、、所在直线分别为、、轴建立如下图所示的空间直角坐标系，

则、、、、、、、，
，，
设平面的法向量为，则，
取，可得，
又因为，则，所以，，
又因为平面，所以，平面.
（2）解：依题意，设，则，
所以，，，
由已知，得，
整理可得，解得或，
所以，线段的长为或.
20．(1)
(2)直线与圆相离，理由见解析

【分析】（1）由题意列出椭圆中的，，的关系解方程组即可求解；
（2）需判断圆心到直线的距离与圆的半径的大小系，重视设而不求的思想方法.
【详解】（1）由题意，圆与轴的交点为，可得，
椭圆上的点到焦点距离的最大值为，
又因为，可得，
，
所以椭圆的标准方程为
（2）如图所示，设，

当直线的斜率存在时，
设直线，
与联立可得，
，
且有，

，
由可得点为中点，可得，
且有，
所以可得，，
即点的坐标为，
将点代入椭圆，可得，
化简后，得，
由于点分别满足，
代入上式可得，，即.
代入韦达定理可得，，满足式，
点到直线的距离，
由于，可得，
所以，
所以有，所以直线与圆相离，
当直线的斜率不存在时，此时有，
代入，
可得，又，可得，
所以直线的方程为，也满足直线与圆相离.
综上，直线与圆相离.
21．(1)
(2)，理由见解析

【分析】（1）根据题意，由单调递增，转化为恒成立，然后分，，讨论，即可得到结果；
（2）根据题意，由（1）可得时，，然后再由放缩，裂项即可得到结果.
【详解】（1）由可得，，
由于函数单调递增，则恒成立，
设，则，
当时，，可知时，，不满足题意；
当时，，函数单调递增，
又因为，即，不满足题意；
当时，令，解得，
当时，，函数单调递减，
当时，，函数单调递增，
所以当时，函数取得最小值，
由可得，，令，则，
可知时，，函数单调递增；
当时，，函数单调递减，
则，由于恒成立，
所以，当且仅当时取等号，
故函数单调递增时，实数的值为.
（2）.
理由如下：
由（1）可知，当时，，即有，
则时，，
故当且时，
，
因为时，，
所以，
则，
所以.
22．(1)；.
(2).

【分析】（1）由题意，参数方程与普通方程互化，极坐标方程与直角坐标方程互化即可；
（2）圆与圆没有公共点，即内含或外离，排除外离，由内含的条件求解即可.
【详解】（1）因为曲线的参数方程为，
平方得：，
由于，所以，又，所以.
所以.
所以的普通方程为：；
曲线的极坐标方程为：，
所以，
所以的直角坐标方程为：.
（2）  
联立得：，
，所以.
若曲线，有公共点，.
因为曲线，没有公共点，所以.
故a的取值范围为：.
23．(1)
(2)证明见解析

【分析】（1），根据绝对值三角不等式可求解；
（2）利用“乘1法”证明，又，利用基本不等式证明即可.
【详解】（1），当时取等号，
∵，，∴，
∴由题可知，∴.
（2），
当且仅当时等号成立.
，
当且仅当时等号成立.
∴．