2024年高考数学一轮复习第一章第二讲充分条件与必要条件课件

这是一份2024年高考数学一轮复习第一章第二讲充分条件与必要条件课件，共24页。PPT课件主要包含了答案D，断性问题，¬q的，p故选A，答案A，图1-2-1，答案C，即x1＜x＜2，答案2＋∞等内容，欢迎下载使用。
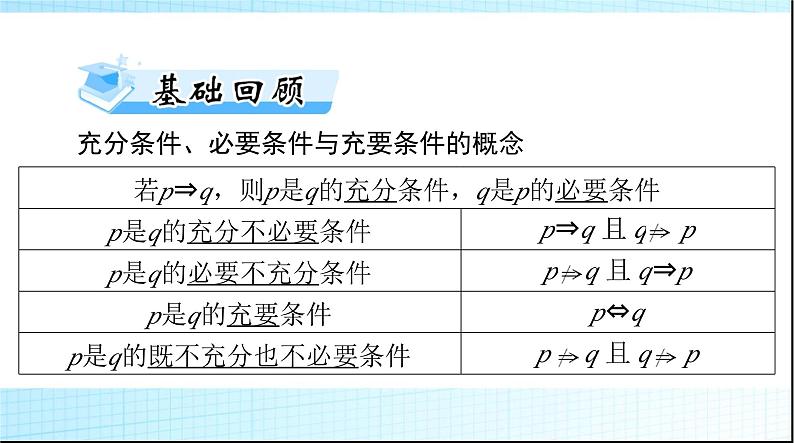
充分条件、必要条件与充要条件的概念
充分条件、必要条件的判断
[例 1](1)(2022 年浙江)设 x∈R，则“sin x＝1”是“cs x＝0”
A.充分不必要条件C.充要条件
B.必要不充分条件D.既不充分也不必要条件
解析：①当 sin x＝1 时，则 cs x＝0，∴充分性成立；②当 cs x＝0 时，则 sin x＝±1，∴必要性不成立，∴“sin x＝1”是“cs x＝0”的充分不必要条件.故选 A.答案：A
(2)王安石在《游褒禅山记》中写到“世之奇伟、瑰怪，非常之观，常在于险远，而人之所罕至焉，故非有志者不能至也”，
请问“有志”是“能至”的(A.充要条件B.既不充分也不必要条件C.充分不必要条件D.必要不充分条件
解析：“故非有志者不能至也”表明“能至”必为“有志”，所以“有志”是“能至”的必要条件；但“有志”也不一定“能至”，所以“有志”是“能至”的必要不充分条件.
【题后反思】判断充分、必要条件的两种方法
(1)定义法：根据 p⇒q，q⇒p 进行判断，适用于定义、定理判
(2)集合法：根据 p，q 成立的对象的集合之间的包含关系进行
判断，多适用于命题中涉及字母范围的推断问题.
【变式训练】1.给定两个命题 p，q，若¬p 是 q 的必要不充分条件，则 p 是
解析：因为¬p 是q的必要不充分条件，所以q⇒¬p，但¬p
所以等价于 p⇒¬q，但¬q
2.(2022 年广州市校级月考)有且只有一个实数λ，使得“b＝
λa”是“向量 b 与向量 a 共线”的(
A.必要不充分条件C.充要条件
B.充分不必要条件D.既不充分也不必要条件
解析：若有且只有一个实数λ，使得 b＝λa，则 a∥b 成立，所以充分性成立；若 a＝0，则 a∥b 成立，但 b＝λa 不一定成立，即必要性不成立.故选 B.答案：B
充分条件、必要条件的应用
考向 1 充分条件、必要条件的探求通性通法：先求使结论成立的充要条件，然后根据“以小推大”的方法确定符合题意的条件.
[例 2](2022 年深圳市期末)已知直线 m，n 与平面α，β，γ，则
能使α⊥β成立的充分条件是(A.α⊥γ，β⊥γB.m∥α，m∥βC.m∥α，m⊥βD.m⊥n，α∩β＝m，n⊂β
解析：对于 A，平面间的垂直关系，不具有传递性，故 A 错误；对于 B，若 m∥α，m∥β，则α∥β或α与β相交，故 B 错误；对于 C，若 m∥α，则必在α中存在直线 l∥m，
因为 m⊥β，则 l⊥β，故α⊥β，故 C 正确；
对于D，如图1-2-1，在长方体ABCD-EFGH 中，平面 ADHE∩平面 BDHF＝HD，AD⊥HD，HD⊂平面 ADHE，但平面 ADHE 与平面 BDHF 不垂直，故 D 错误.故选 C.
考向 2 利用充分、必要条件求参数的取值范围
通性通法：(1)巧用转化求参数：把充分条件、必要条件或充要条件转化为集合之间的关系，然后根据集合之间的关系列出关于参数的不等式(或不等式组)求解.
(2)端点取值慎取舍：在求参数范围时，要注意边界或区间端
点值的检验，从而确定取舍.
[例3] 已知集合P＝{x|－2≤x≤10}，非空集合S＝{x|1－m≤x≤1＋m}.若“x∈P”是“x∈S”的必要条件，则m的取值范围是________.
解析：由“x∈P”是“x∈S”的必要条件，知 S⊆P.
∴0≤m≤3.即 m 的取值范围是[0，3].答案：[0，3]
2.(考向 2)设 p：1＜x＜2；q：(x－a)(x－1)≤0.若 p 是 q 的充分不必要条件，则实数 a 的取值范围是________.
解析：由题意知{x|1＜x＜2}
{x|(x－a)(x－1)≤0}，则 a＞1，
{x|1≤x≤a}，从而 a≥2.
⊙“交汇型”充分条件、必要条件的判断[例 4]已知等差数列{an}的公差为 d，前 n 项和为 Sn，则“d＞
0”是“S4＋S6＞2S5”的(　　)A.充分不必要条件C.充要条件
【反思感悟】“交汇型”充分条件、必要条件的问题通常是选取合适的数学背景，把新交汇考点巧妙地融入试题中.虽然它的构思巧妙、题意新颖，但是，它考查的还是基本知识和基本技能.解这类题的关键在于用慧眼去找寻“交汇点”，用心灵去感受题意以及科学合理地运算推理.
【高分训练】1.(2021 年青岛市期末)“a＞2”是“函数f(x)＝ax＋lgax(a＞
0，a≠1)在(0，＋∞)上单调递增”的(A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
解析：因为函数 f(x)＝ax＋lgax(a＞0，a≠1)在(0，＋∞)上单调递增，结合指数函数和对数函数的单调性可得 a＞1，又因为(2，
(1，＋∞)，所以“a＞2”是“函数f(x)＝ax＋lgax(a＞0，
a≠1)在(0，＋∞)上单调递增”的充分不必要条件.故选 A.