《建立一元二次方程解决几何问题》课后习题-九年级上册数学北师大版

这是一份《建立一元二次方程解决几何问题》课后习题-九年级上册数学北师大版，共3页。
2.6 应用一元二次方程(1)一、初步探究如图，一个长为10米的梯子斜靠在墙上，梯子的顶端距地面的垂直距离为8米。• 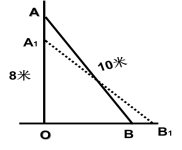                    如果梯子顶端下滑1米时，梯子底端滑动的距离等于1米吗？•                     那么梯子顶端下滑几米时，梯子底端滑动的距离和它相等呢？   •                     根据以上问题：如果梯子长度是13米，梯子顶端与地面的垂直距离12米,梯子顶端下滑的距离与梯子底端滑动的距离可能相等吗？如果相等，那么这个距离是多少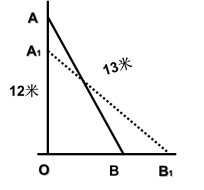？ A1[ 二、合作探究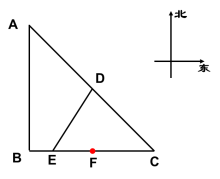如图,小明游览于点A处,在其正南方向200米处有一座灯塔B,在B的正东方向200米处是通往古象馆的渡轮C， 托孤堂D位于AC的中点,小华此时正在D处游览;凉亭 F位于BC的中点，小明从A出发,经B到C匀速行驶,小华同时从D出发,沿南偏西方向匀速直线行驶，打算和小明汇合。已知小明的速度是小华的2倍,小明由B到C的途中与小华相遇于E处,那么他们相遇时小华走了多少米?(结果精确到0.1米)   小组讨论:（1）仔细审题，将题目中的关键信息勾画出来，将已知量和未知量标注在图中；（2）你能用图中已有线段（或线段的和）来表示小明、小华所走的路程吗？二者有什么样的关系？（3）BC的中点F对建立相等关系有什么作用？（4）你准备设什么为未知数？如何建立方程？      三、牛刀小试根据下面文字您能猜出周瑜去逝时的年龄吗？大江东去浪淘尽，千古风流人物。而立之年督东吴，英年早逝两位数。十位恪小个位三，个位平方与寿符。哪位学子算得快，多少年华周瑜属？A.25       B.36      C.47        D.58四、学以致用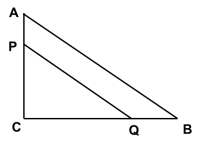如图，猴区里有一颗大树，树上离地面6米的A处有一只猕猴P,地面上距树底部C 8米的B处有另一只猕猴Q，现在他们都以1米/秒的速度同时向树底部C移动，几秒后的面积为面积的一半？    五、归纳小结通过本节课的学习，你有哪些收获呢?六、作业布置习题2.9：知识技能1,3.