第一章勾股定理中典型题与思想方法课件-(北师大)

这是一份第一章勾股定理中典型题与思想方法课件-(北师大)，共17页。

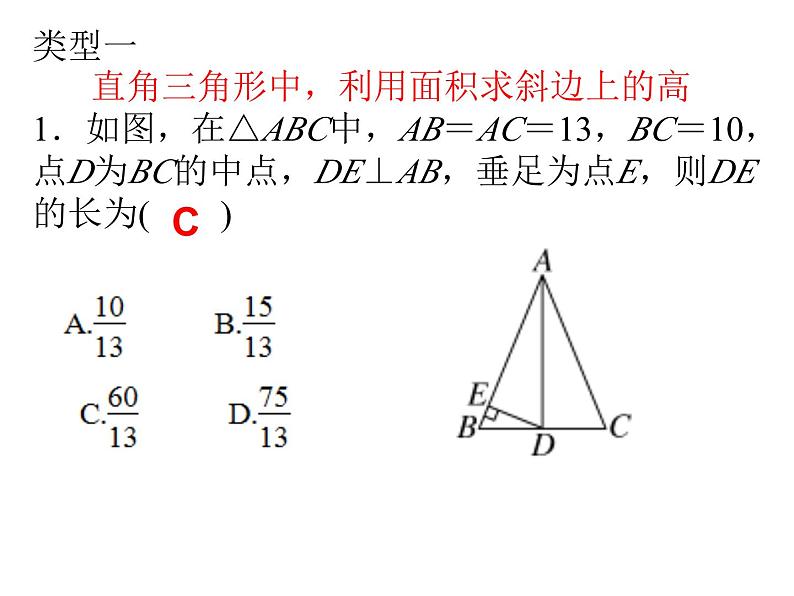
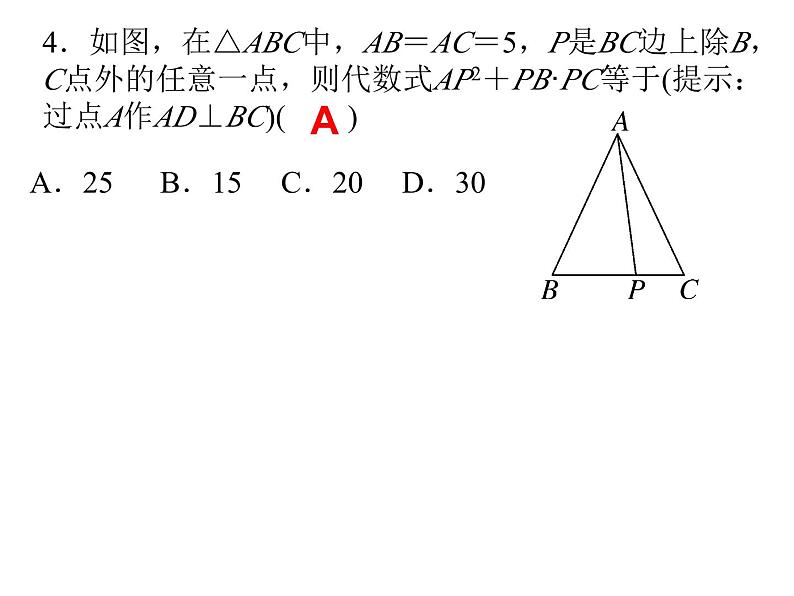
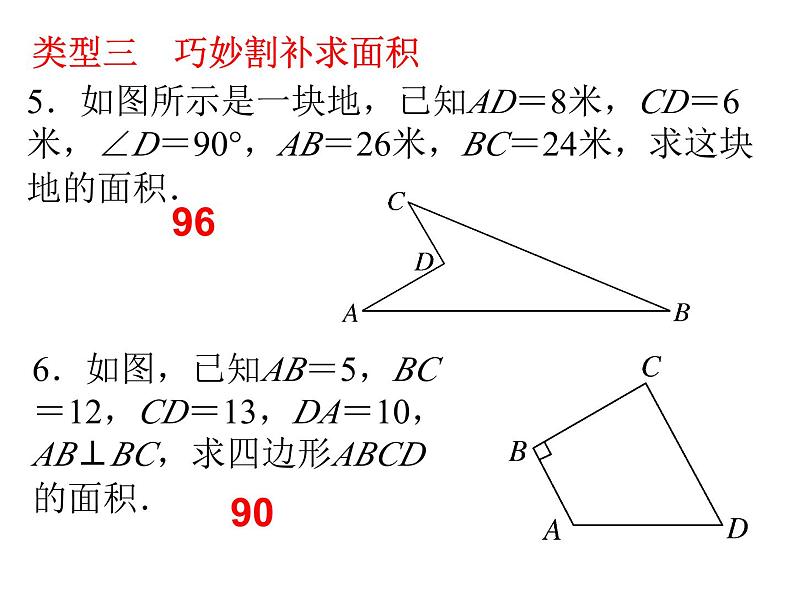
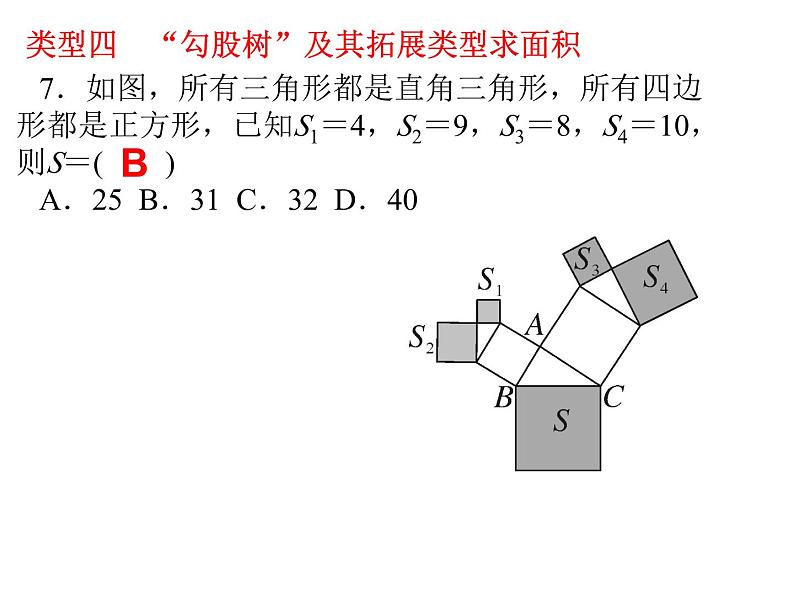
勾股定理典型题与思想方法勾股定理与面积问题类型一　 直角三角形中，利用面积求斜边上的高1．如图，在△ABC中，AB＝AC＝13，BC＝10，点D为BC的中点，DE⊥AB，垂足为点E，则DE的长为(　　)C2．如图，在△ABC中，∠ACB＝90°，AB＝5，BC＝3，CD⊥AB，垂足为D，则CD的长为________．类型二　结合乘法公式巧求面积或长度3．已知Rt△ABC中，∠C＝90°，若a＋b＝7cm，c＝5cm，则Rt△ABC的面积是(　　)A．6cm2 B．9cm2 C．12cm2 D．15cm22.4A类型二　结合乘法公式巧求面积或长度3．已知Rt△ABC中，∠C＝90°，若a＋b＝7cm，c＝5cm，则Rt△ABC的面积是(　　)A．6cm2 B．9cm2 C．12cm2 D．15cm2A4．如图，在△ABC中，AB＝AC＝5，P是BC边上除B，C点外的任意一点，则代数式AP2＋PB·PC等于(提示：过点A作AD⊥BC)(　　)A．25 B．15 C．20 D．30A类型三　巧妙割补求面积5．如图所示是一块地，已知AD＝8米，CD＝6米，∠D＝90°，AB＝26米，BC＝24米，求这块地的面积． 6．如图，已知AB＝5，BC＝12，CD＝13，DA＝10，AB⊥BC，求四边形ABCD的面积．9690类型四　“勾股树”及其拓展类型求面积7．如图，所有三角形都是直角三角形，所有四边形都是正方形，已知S1＝4，S2＝9，S3＝8，S4＝10，则S＝(　　)A．25 B．31 C．32 D．40B 8．“赵爽弦图”是四个全等的直角三角形与中间一个正方形拼成的大正方形．如图，每一个直角三角形的两条直角边的长分别是3和6，则大正方形与小正方形的面积差是(　　)A．9 B．36 C．27 D．34B9．如图所示的大正方形是由八个全等的直角三角形和一个小正方形拼接而成，记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若正方形EFGH的边长为2，则S1＋S2＋S3＝________．1210．★五个正方形按如图放置在直线l上，其中第1，2，4个正方形的面积分别为2，5，4，则第5个正方形的面积S5＝________．1勾股定理中的思想方法类型一　分类讨论思想一、直角边和斜边不明时需分类讨论1．在一个直角三角形中，若其中两边长分别为5，3，则第三边长的平方为(　　)A．16 B．16或34 C．34 D．不存在2．已知x，y为正数，且|x－4|＋(y－3)2＝0，如果以x，y为边长作一个直角三角形，那么以这个直角三角形的斜边长为边长的正方形的面积为(　　)A．5 B．7 C．7或25 D．16或25BD二、锐角和钝角不明时需分类讨论3．在△ABC中，AB＝13cm，AC＝20cm，BC边上的高为12cm，则△ABC的面积为________cm2.变式训练：等腰三角形的腰长为5，一腰上的高为3，则这个等腰三角形底边长的平方为________．三、腰和底不明时需分类讨论4．★如图，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3，将△ABC扩充为等腰△ABD，且扩充部分是以AC为直角边的直角三角形，则CD的长为(　　)126或6690或10A类型二　方程思想一、利用两直角三角形“公共边”相等列方程5．如图，在△ABC中，CD⊥AB于D，若AD∶BD＝5∶2，AC＝17，BC＝10，则BD的长为(　　)A．4 B．5 C．6 D．86．如图，在△ABC中，AB＝15cm，AC＝13cm，BC＝14cm，则△ABC的面积为________cm2C84二、折叠问题中利用勾股定理列方程7．如图，在Rt△ABC中，∠B＝90°，AB＝3，BC＝4，将△ABC折叠，使点B恰好落在边AC上与点B′重合，AE为折痕，则EB＝________．8．如图，长方形纸片ABCD沿对角线AC折叠，设点D落在D′处，BC交AD′于点E，AB＝6cm，BC＝8cm，求阴影部分的面积．类型三　利用转化思想求最值9．课外小组的同学在学校的花园里观察到一棵牵牛花的藤在一截面周长为36cm的圆柱形水管上缠绕4圈后，恰好上升至108cm的高度，则此时牵牛花藤的长度至少是________．10．如图是一个三级台阶，它的每一级长、宽、高分别是100cm，15cm和10cm，A，B是这个台阶上两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿台阶爬行到B点的最短路程是________．180cm125cm