12.1全等三角形 课件 人教版数学八年级上册

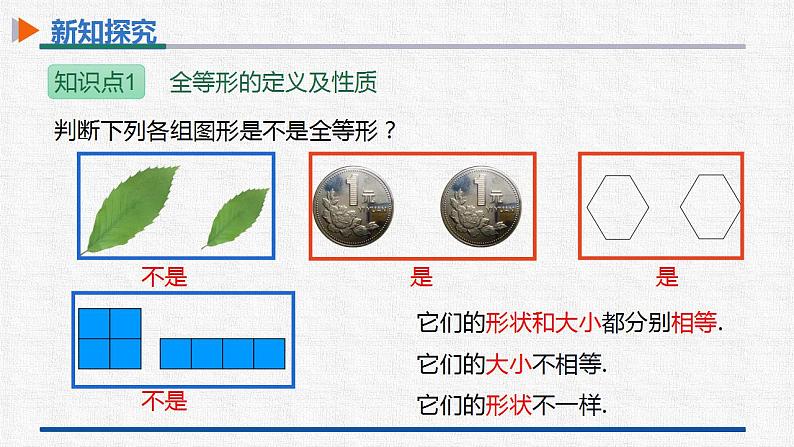
第十二章 全等三角形12.1 全等三角形 学习目标-新课导入-新知探究-课堂小结-课堂训练 学习目标1.理解并掌握全等三角形的概念及其基本性质.（重点）2.能正确表示两个全等三角形，能找准全等三角形的对应边、对应角.（难点）3.能利用全等三角形的性质进行简单的推理和计算，并解决一些实际问题.（难点） 新课导入情景引入暑假爸爸妈妈带我去了海洋馆!用数码相机拍了很多漂亮的照片.我选了最喜欢的三张，每张都洗了同样大小的两张，打算送给我的两个好朋友！拿到照片之后，我发现每两张同样的照片有一个共同点，妈妈还告诉我，在数学上，它们有一个共同的名字.你们一定想知道吧！学习了今天的这节课，答案就揭晓了! 新课导入情景引入 新知探究①②③④观察下列四组图形，他们的形状和大小有什么特点？归纳：1、形状相同；2、大小相同；3、能够完全重合.定义：能够完全重合的两个图形叫做全等形. 新知探究判断下列各组图形是不是全等形？不是是是不是它们的形状和大小都分别相等.它们的大小不相等.它们的形状不一样. 新知探究你能举出一些生活中的全等形吗？全等形的性质：如果两个图形全等，它们的形状和大小一定都相等. 新知探究怎样用纸板剪出两个三角形，使这两个三角形是全等形？剪一剪 新知探究像这样，能够完全重合的两个三角形,叫作全等三角形.全等三角形中的对应元素：把两个全等的三角形重合到一起，重合的顶点叫做对应顶点，重合的边叫做对应边，重合的角叫做对应角. 新知探究对应顶点：点A与点D，点B与点E，点C与点F.对应边：AB与DE，AC与DF，BC与EF.对应角：∠A与∠D，∠B与∠E，∠C与∠F. 新知探究如图，△ABC和△DEF全等，点A与点D，点B与点E，点C与点F是对应点，记作△ABC≌△DEF ,读作三角形ABC全等于三角形DEF. 全等用符号“≌”表示，读作“全等于”.注意： 记两个三角形全等时，通常把对应顶点的字母写在对应的位置上. △ABC≌△FDE 新知探究给你用纸板剪出的两个全等三角形标上顶点，与你的同伴说一说你的全等三角形应该怎么表示，它们的对应顶点、对应边和对应角分别是什么？ 新知探究思考：将△ABC沿直线BC平移，得到△DEF，这两个三角形全等吗？1、△ABC与△DEF大小相等.2、△ABC与△DEF形状相同.3、△ABC与△DEF完全重合.结论：三角形经过平移后，位置发生了变化，但是大小、形状没有发生变化，平移前后的两三角形全等. 新知探究思考：将△ABC沿直线BC翻折180°，得到△DBC，这两个三角形全等吗？1、△ABC与△DBC大小相等.2、△ABC与△DBC形状相同.3、△ABC与△DBC完全重合.结论：三角形经过翻折后，位置发生了变化，但是大小、形状没有发生变化，翻折前后的两三角形全等.D 新知探究思考：△ABC绕点A旋转，得到△ADE，这两个三角形全等吗？1、△ABC与△ADE大小相等.2、△ABC与△ADE形状相同.3、△ABC与△ADE完全重合.结论：三角形经过平移后，位置发生了变化，但是大小、形状没有发生变化，平移前后的三角形全等.A 新知探究由于全等三角形形状、大小都一样，所以全等三角形的对应边相等，对应角相等. 新知探究全等三角形的性质的几何语言∵△ABC≌△DEF，∴AB=DE，AC=DF，BC=EF；（全等三角形对应边相等）∠A=∠D，∠B=∠E，∠C=∠F.（全等三角形对应角相等） 新知探究例 如图.（1)若△BOD≌△COE，∠B=∠C，指出这两个全等三角形中其余相等的边和角；解：∵△BOD≌△COE，∠B=∠C，∴BO=CO，OD=OE，BD=CE；∠DOB=∠EOC，∠BDO=∠CEO.对顶角是对应角. 新知探究解：∵△ADO≌△AEO，AD=AE，∴AO=AO，OD=OE；∠DOA=∠EOA，∠ADO=∠AEO，∠DAO=∠EAO.例 如图.（2）若△ADO≌△AEO，AD=AE，指出这两个全等三角形中其余相等的边和角；公共边是对应边. 新知探究解：∵△ABO≌△ACO，AB=AC，∴AO=AO，OB=OC；∠B=∠C，∠AOB=∠AOC，∠BAO=∠CAO.例 如图.（3）若△ABO≌△ACO，AB=AC，指出这两个全等三角形中其余相等的边和角；公共边是对应边. 新知探究解：∵△ABE≌△ACD，AE=AD，∴AB=AC，EB=DC；∠B=∠C，∠BAE=∠CAD，∠BEA=∠CDA.例 如图.（4）若△ABE≌△ACD，AE=AD，指出这两个全等三角形中其余相等的边和角.公共角是对应角.1.（1）如图，已知△ABC≌△DEF，∠B=50°，∠C=60°，则∠E=　 ．（2）请根据图中提供的信息，写出x=　 　．跟踪训练 新知探究50°20用“≌”表示两个全等三角形，可根据字母的对应位置找对应关系.2.如图，点B、F、C、E在同一直线上，△ABC≌△DEF．（1）求证：AB∥DE；（2）若CE=2.2，BC=4.5，求CF的长．跟踪训练 新知探究（1）证明：∵△ABC≌△DEF，∴∠B=∠E，∴AB∥DE；（2）解：∵△ABC≌△DEF，∴BC=EF=4.5.∴BC﹣CF=EF﹣CF,即BF=CE.∴BF=2.2.∴CF=BC﹣BF=4.5﹣2.2=2.3． 新知探究2.全等三角形中，公共角一定是对应角.（如图④）3.全等三角形中，对顶角一定是对应角.（如图⑤⑥） ⑤ ⑥4.全等三角形中，最长（最短）的边与最长（最短）的边是对应边，最大（最小）的角与最大（最小）的角是对应角. 新知探究寻找对应边、对应角的规律5. 对应角所对的边为对应边；对应边所对的角为对应角.6. 两个对应角所夹的边为对应边；两条对应边所夹的角为对应角.7.若用“≌”表示两个全等三角形，可根据字母的对应位置找对应关系. 新知探究寻找对应边、对应角的规律 课堂小结全等三角形能够完全重合的两个三角形叫做全等三角形用全等符号“≌”表示对应边相等，对应角相等对应顶点、对应边、对应角 课堂训练1．下列说法不正确的是（　　）A．如果两个图形全等，那么它们的形状和大小一定相同 B．面积相等的两个图形是全等图形 C．图形全等，只与形状、大小有关，而与它们的位置无关 D．全等三角形的对应边相等，对应角相等B 课堂训练2．下列图形中与如图图形全等的是（　　）C 课堂训练3．如图，Rt△ABC沿直角边BC所在直线向右平移到Rt△DEF，则下列结论中，错误的是（　　）A．BE=EC B．BC=EF C．AC=DF D．△ABC≌△DEF【解析】∵Rt△ABC沿直角边BC所在直线向右平移到Rt△DEF，∴Rt△ABC≌Rt△DEF.∴BC=EF，AC=DF.∴BC-EC=EF-EC，即BE=CF.所以只有选项A是错误的.故选A．A 课堂训练4．（2021•哈尔滨）如图，△ABC≌△DEC，点A和点D是对应顶点，点B和点E是对应顶点，过点A作AF⊥CD，垂足为点F，若∠BCE＝65°，则∠CAF的度数为（　　）A．30° B．25° C．35° D．65°【解析】∵△ABC≌△DEC，∴∠ACB=∠DCE.∵∠BCE=65°，∴∠ACD=∠BCE=65°.∵AF⊥CD，∴∠AFC=90°.∴∠CAF=90°﹣65°=25°.故选B．B 课堂训练∵△ABC≌△AEF，∴∠2＝∠1，则∠2-∠EAC＝∠1-∠EAC，即∠3＝∠4.旋转型 课堂训练5．如图，△ABC≌△ADC，∠ABC＝118°，∠DAC＝40°，则∠BCD的度数为　 　°．【解析】∵△ABC≌△ADC，∴∠ABC＝∠ADC＝118°，∠ACB＝∠ACD．∴∠ACD＝180°﹣∠ADC﹣∠DAC＝22°．∴∠ACB＝22°．∴∠BCD＝∠ACB+∠ACD＝44°．故答案为44．44 课堂训练6．如图，△ACD≌△CBE，且点D在边CE上．若AD＝24，BE＝10，则DE的长为 　 　．【解析】∵△ACD≌△CBE，AD=24，BE=10，∴CE=AD=24，CD=BE=10，∴DE=CE﹣CD=24﹣10=14.故答案为14．14 课堂训练7．如图，在△ABC中，D，E分别是AC，AB上的点，若△ADE≌△BDE≌△BDC，则∠DBC的度数为　 　．【解析】∵△ADE≌△BDE≌△BDC，∴∠A=∠DBE=∠CBD，∠AED=∠BED=∠C．∵∠AED+∠BED=180°，∴∠AED=∠BED=90°=∠C．∴在Rt△ABC中，∠A+∠CBA=180°,即3∠A=90°．∴∠A=30°．∴∠DBC=∠A=30°．故答案为30°．30° 课堂训练8．如图，D、A、E三点在同一条直线上，BD⊥DE于点D，CE⊥DE于点E，且△ABD≌△CAE，AC＝4．（1）求∠BAC的度数；解：∵BD⊥DE，∴∠D＝90°.∴∠DBA+∠BAD＝90°.∵△ABD≌△CAE，∴∠DBA＝∠CAE.∴∠BAD+∠CAE＝90°，∴∠BAC＝90°. 课堂训练8．如图，D、A、E三点在同一条直线上，BD⊥DE于点D，CE⊥DE于点E，且△ABD≌△CAE，AC＝4．（2）求△ABC的面积； 课堂训练8．如图，D、A、E三点在同一条直线上，BD⊥DE于点D，CE⊥DE于点E，且△ABD≌△CAE，AC＝4．（3）求证：DE=CE+BD.证明：∵△ABD≌△CAE，∴BD＝AE，AD＝CE.∵DE=AD+AE，∴DE=CE+BD. 课堂训练∵△ABC≌△CEF，∴易得△ACF为等腰直角三角形.一线三等角型