



初中人教版第十二章 全等三角形12.2 三角形全等的判定说课ppt课件
展开1.探索并正确理解三角形全等的判定方法“SAS”.(重点)2.会用“SAS”判定方法证明两个三角形全等及进行简单的应用.(重点)3.了解“SSA”不能作为两个三角形全等的条件.(难点)
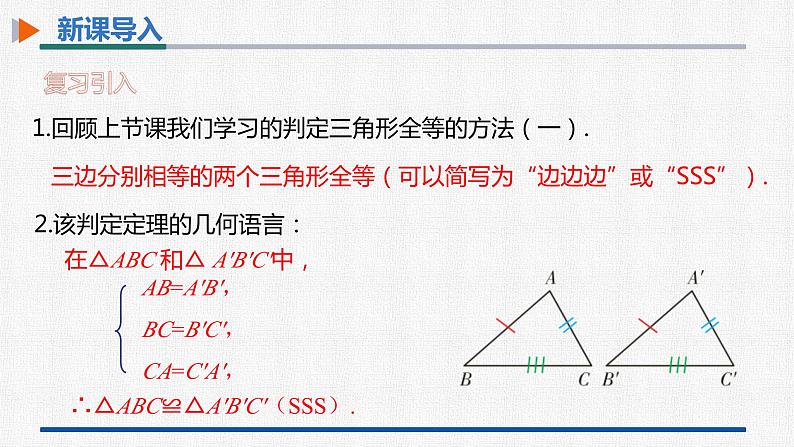
1.回顾上节课我们学习的判定三角形全等的方法(一).
2.该判定定理的几何语言:
在△ABC 和△ A'B'C'中,
∴△ABC≌△A'B'C'(SSS).
三边分别相等的两个三角形全等(可以简写为“边边边”或“SSS”).
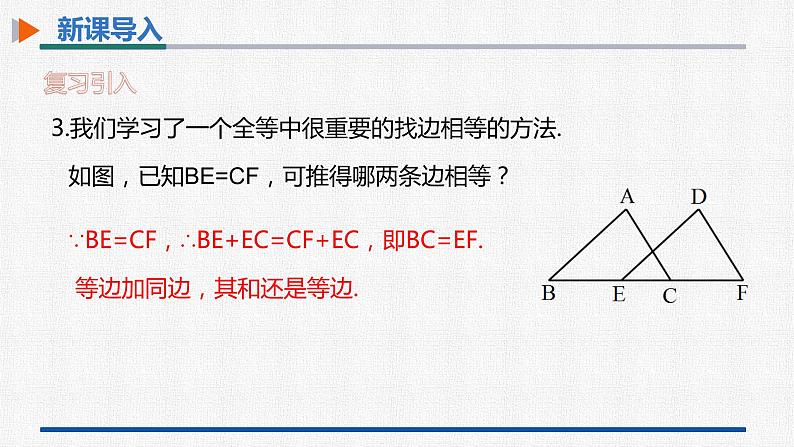
3.我们学习了一个全等中很重要的找边相等的方法.
∵BE=CF,∴BE+EC=CF+EC,即BC=EF.
如图,已知BE=CF,可推得哪两条边相等?
等边加同边,其和还是等边.
4.(1)当两个三角形满足六个条件中“一个或两个对应条件相等”时,两个三角形均 .
除了这两种情况,还有其他情况吗?
③两条边和一个角对应相等;④两个角和一条边对应相等
(2)当满足六个条件中的“三个对应条件相等”时,已经讨论了以下两种情况:
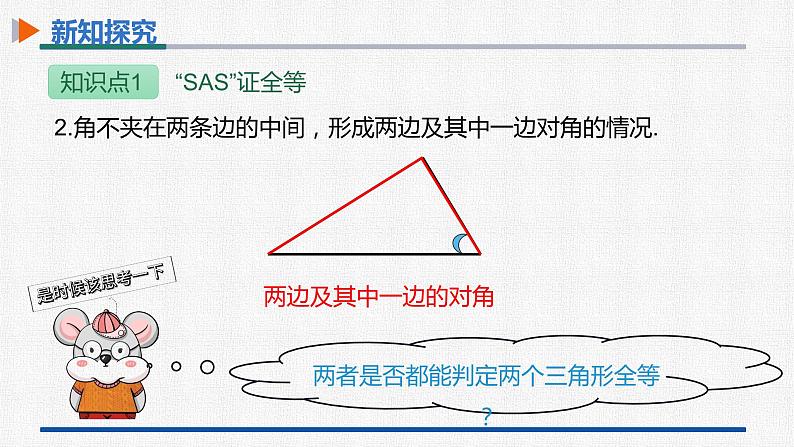
1.角夹在两条边的中间,形成两边夹一角的情况.
两者是否都能判定两个三角形全等?
2.角不夹在两条边的中间,形成两边及其中一边对角的情况.
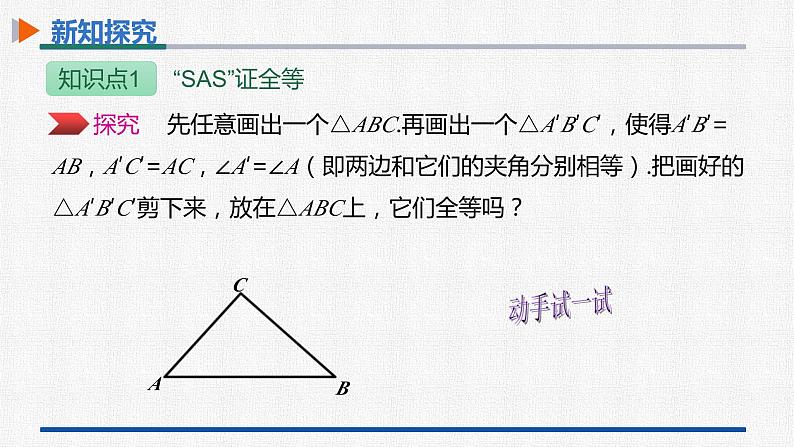
作法:(1)画∠DA'E=∠A;(2)在射线A'D上截取A'B'=AB,在射线A'E上截取A'C'=AC;(3)连接B'C '.
思考 ① △A′B′C′ 与△ABC全等吗?
②这两个三角形全等满足的是哪三个条件?
∴△ABC≌△A'B'C'(SAS).
该判定定理的几何语言:
注意:必须是两边的夹角
就也是说,三角形的两条边的长度和它们的夹角的大小确定了,这个三角形的形状、大小就确定了.
例 如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和点B.连接AC并延长到点D,使CD=CA.连接BC并延长到点E,使得CE=CB.连接DE,那么量出DE的长就是A,B的距离.为什么?
【分析】如果能证明△ABC≌△DEC,就可以得出AB=DE.由题意可知,△ABC和△DEC具备“边角边”的条件.
证明:在△ABC 和△DEC中,
∴△ABC≌△DEC(SAS),∴AB=DE.
(2021•陕西)如图,BD∥AC,BD=BC,点E在BC上,且BE=AC.求证:∠D=∠ABC.
思考 如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC.固定住长木棍,转动短木棍,得到△ABD.这个实验说明了什么?
△ABC和△ABD满AB=AB ,AC=AD,∠B=∠B,但△ABC与△ABD不全等.
三角形的全等的判定(二)(SAS)
两边和它们的夹角分别相等的两个三角形全等
1.已知两边,必须找“夹角”2. 已知一角和这角的一夹边,必须找这角的另一夹边
1.下列条件中,不能证明△ABC≌△DEF的是( )A.AB=DE,∠B=∠E,BC=EFB.AB=DE,∠A=∠D,AC=DFC.BC=EF,∠B=∠E,AC=DFD.BC=EF,∠C=∠F,AC=DF
2.(2021•福建)如图,在△ABC中,D是边BC上的点,DE⊥AC,DF⊥AB,垂足分别为E,F,且DE=DF,CE=BF.求证:∠B=∠C.
3.(2021•广东二模)如图,AC=AB,AE=AD,∠3=∠4,求证:∠1=∠2.
4.(2021•宜宾)如图,已知OA=OC,OB=OD,∠AOC=∠BOD.求证:△AOB≌△COD.
5.(2021•泰兴市模拟)如图,点D,E分别在AB,AC上,BE,DC相交于点F, .求证:∠B=∠C.在“①AB=AC;②BE=CD;③AD=AE”这三个条件中选择两个填入上面的横线上(只要填写序号),并完成解答.
6.如图,点D、E、F、B在同一直线上,DF=BE,CE=AF,EC∥AF.(1)求证:CD=AB;
6.如图,点D、E、F、B在同一直线上,DF=BE,CE=AF,EC∥AF.(2)若∠A=30°,∠D=40°,求∠DEC的度数.
解:由(1)得△CED≌△AFB,∴∠C=∠A=40°,∴∠DEC=180°﹣(∠D+∠C)=180°﹣(30°+40°)=110°.
7.(2021•大连)如图,点A,D,B,E在一条直线上,AD=BE,AC=DF,AC∥DF.求证:BC=EF.
8.如图,已知CA=CB,AD=BD, M,N分别是CA,CB的中点,求证:DM=DN.
在△CAD与△CBD中,
∴△ACD≌△BCD(SSS).
证明:如图,连接CD.
又∵M,N分别是CA,CB的中点,
在△AMD与△BND中,
∴△AMD≌△BND(SAS).
9.(2021•咸宁一模)如图,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P.(1)求证:△ABM≌△BCN.
初中数学人教版八年级上册12.2 三角形全等的判定备课ppt课件: 这是一份初中数学人教版八年级上册<a href="/sx/tb_c10244_t3/?tag_id=26" target="_blank">12.2 三角形全等的判定备课ppt课件</a>,共24页。PPT课件主要包含了知识回顾,学习目标,课堂导入,新知探究,跟踪训练,随堂练习,三角形全等的判定,对比探究,课堂小结,拓展提升等内容,欢迎下载使用。
初中数学12.2 三角形全等的判定评课课件ppt: 这是一份初中数学<a href="/sx/tb_c10244_t3/?tag_id=26" target="_blank">12.2 三角形全等的判定评课课件ppt</a>,共23页。PPT课件主要包含了知识回顾,学习目标,课堂导入,新知探究,跟踪训练,ABED,∠ACB∠ECD,随堂练习,三角形全等的判定,分类探讨等内容,欢迎下载使用。
初中数学人教版八年级上册12.2 三角形全等的判定背景图课件ppt: 这是一份初中数学人教版八年级上册<a href="/sx/tb_c10244_t3/?tag_id=26" target="_blank">12.2 三角形全等的判定背景图课件ppt</a>,共24页。PPT课件主要包含了知识回顾,学习目标,课堂导入,新知探究,跟踪训练,∠DAB∠CBA,随堂练习,三角形全等的判定,分类探讨,SAS等内容,欢迎下载使用。













