初中数学人教版八年级上册13.3.2 等边三角形评课ppt课件

这是一份初中数学人教版八年级上册13.3.2 等边三角形评课ppt课件，共32页。PPT课件主要包含了学习目标，新课导入，复习引入，两边相等，性质1，等边对等角，三线合一，性质2，等腰三角形，定义两边相等等内容，欢迎下载使用。

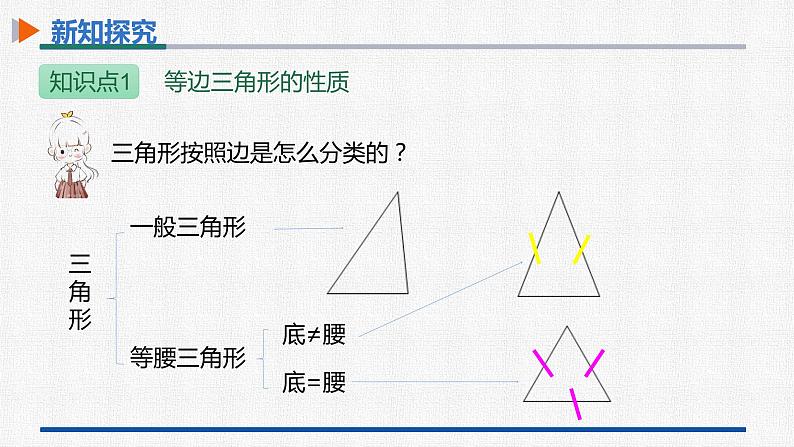
1.探索并掌握等边三角形的性质和判定．（重点）2.能运用等边三角形的性质和判定进行计算和证明．（难点）
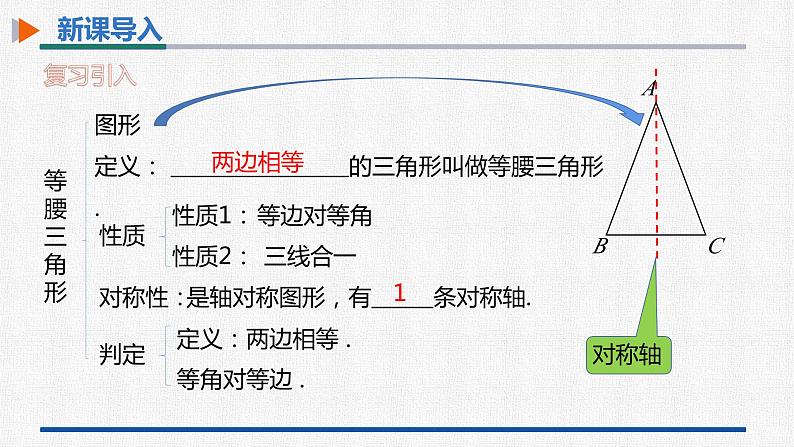
定义： 的三角形叫做等腰三角形.
是轴对称图形，有 条对称轴.
思考1 把等腰三角形的性质1（等边对等角）用于等边三角形，能得到什么结论？
三角形内角和为180°
∠A=∠B=∠C=60°
BC边上的中线,高和所对角的平分线“三线合一”.
AB边上的中线,高和所对角的平分线“三线合一”.
AC边上的中线,高和所对角的平分线“三线合一”.
思考3 把等腰三角形的对称性用于等边三角形，能得到什么结论？
BC边上的中线,高和所对角的平分线所在直线为对称轴.
AB边上的中线,高和所对角的平分线所在直线为对称轴.
AC边上的中线,高和所对角的平分线所在直线为对称轴.
每一边上的中线、高和这一边所对的角的平分线互相重合
底边上的中线、高和顶角的平分线互相重合
例1 如图，△ABC是等边三角形，BD平分∠ABC，延长BC到点E，使得CE=CD．求证：BD=DE．
证明：∵△ABC是等边三角形，BD是角平分线，∴∠ABC=∠ACB=60°，∠DBC=30°．∵CE=CD，∴∠CDE=∠E．又∠ACB=∠CDE+∠E，∴∠CDE=∠E=30°．∴∠DBC=∠E．∴DB=DE．
【变式】如图，已知△ABC是等边三角形，点B，C，D，E在同一直线上，且CG=CD，DF=DE，则∠E=（ ）A.15° B.20° C.25° D.30°
【变式】如图，等边三角形ABC的边长为3，点D是AC的中点，点E在BC的延长线上，若DE=DB，求CE的长.
解：∵△ABC是等边三角形，D是AC的中点，∴∠ABC=∠ACB=60°，BD为∠ABC的平分线，∴∠DBE= ∠ABC=30°. ∵DE=DB，∴∠E=∠DBE=30°.∵∠ACB=∠CDE+∠E,∴∠CDE=∠ACB-∠E=30°.
∴∠CDE=∠E.∴CD=CE.∵等边三角形ABC的边长为3，点D是AC的中点, ∴CE=CD= .
已知：如图，在△ABC中，∠A=∠B=∠C.求证：△ABC是等边三角形.
证明：∵∠A=∠B,∴BC=AC.∵∠B=∠C,∴AC=AB. ∴AB=BC=AC，则△ABC是等边三角形.
等腰三角形只要满足一个角是60°，就可以判定它是等边三角形？你同意这样的说法吗？试着证明一下吧！
证明：∵AB=AC，∠B=60°,∴∠C=∠B=60°. ∴∠A=180°-（∠B+∠C）=60°, ∴∠A=∠B=∠C. ∴△ABC是等边三角形.
已知：如图，在△ABC中，AB=AC，∠B=60°.求证：△ABC是等边三角形.
已知：如图，在△ABC中，AB=AC，∠A=60°.求证：△ABC是等边三角形.
证明：∵AB=AC,∴∠C=∠B. ∵∠A=60°,∴∠B+∠C=180°-∠A=120°. ∴∠A=∠B=∠C=60°. ∴△ABC是等边三角形.
三个角都相等的三角形是等边三角形
有一个角是60°的等腰三角形是等边三角形.
两个角相等的三角形是等腰三角形
两条边相等的三角形是等腰三角形
三条边都相等的三角形是等边三角形
例2 如图，△ABC是等边三角形，DE∥BC，分别交AB，AC于点D，E.求证：△ADE是等边三角形.
证明：∵△ABC是等边三角形，∴∠A=∠B=∠C. ∵DE∥BC,∴∠ADE=∠B，∠AED=∠C. ∴∠A=∠ADE=∠AED. ∴△ADE是等边三角形.
想一想：本题还有其他证法吗？
【变式】如图，△ABC是等边三角形，D，E分别是边AB，AC上一点，且BD=CE.求证：△ADE是等边三角形.
证明：∵△ABC是等边三角形， ∴AB=AC，∠A=60°. ∵BD=CE， ∴AB-BD=AC-CE，即AD=AE, ∴△ADE是等边三角形.
判定一个三角形是等边三角形的方法选择：若已知三边关系，一般选用定义判定；若已知三角关系，一般选用判定方法1；若已知该三角形是等腰三角形，一般选用判定方法2.
等边三角形的性质与判定
三边都相等的三角形是等边三角形.
每条边上都具有“三线合一”性质
是轴对称图形，有3条对称轴
三边都相等的三角形是等边三角形
有一个角是60°的等腰三角形是等边三角形
1.下列条件中不能得到等边三角形的是（ ）A.有一个角是60°的等腰三角形B.三边相等的三角形C.有两个内角是60°的三角形D.有两个外角相等的等腰三角形
2.已知等腰三角形的一边长为8，一个内角为60°，则它的周长为　 　 ．
3.（2021•丹阳市二模）如图，直线l1∥l2，△ABC是等边三角形，若∠1＝40°，则∠2的度数　 　．
4.等边三角形ABC的两条角平分线BD和CE相交于点F，则∠BFC的度数为 　 　 ．
第3题图 第4题图
5.（2021•乐平市一模）如图，在等边三角形ABC中，点D在边AB上，点E在边AC上，将△ADE折叠，使点A落在BC边上的点F处，则∠BDF+∠CEF= .
【解析】根据折叠的性质，得∠DFE＝∠A＝60°.
根据三角形内角和易得∠BDF+∠1＝120°，∠CEF+∠2＝120°.∴∠1＝120°-∠BDF，∠2＝120°-∠CEF.根据平角为180°易得∠1+∠2＝120°.∴∠BDF+∠CEF=120°.故答案为120°．
解：∵△ABC是等边三角形，AD⊥BC，∴BD=CD，∠EDB=∠EDC，∠ACB=60°.又ED=ED，∴△EDB≌△EDC（SAS）.∴∠EBD=∠ECD=45°.∴∠ACE=∠ACB-∠ECD=60°-45°=15°.
6.如图，等边三角形ABC中，AD⊥BC，垂足为D，点E在线段AD上，∠EBC=45°，求∠ACE的度数.
7.如图，在等边三角形ABC中，D，E分别是AB，AC上的点，且AD=CE，则∠BCD+∠CBE的大小是多少？
解：∵△ABC是等边三角形，∴∠ACB=∠A=∠ABC=60°，且AB=BC=AC.又AD=CE，∴△ADC≌△CEB（SAS），∴∠ACD=∠CBE.∴∠BCD+∠CBE=∠BCD+∠ACD=∠ACB=60°.