初中数学人教版八年级上册13.1.2 线段的垂直平分线的性质示范课课件ppt

这是一份初中数学人教版八年级上册13.1.2 线段的垂直平分线的性质示范课课件ppt，共23页。PPT课件主要包含了学习目标，新课导入，复习引入，轴对称图形，两个图形成轴对称，新知探究，2作直线CD，跟踪训练，课堂小结，作对称轴等内容，欢迎下载使用。

1.能用尺规准确地作出已知线段的垂直平分线．(重点）2.进一步了解尺规作图的一般步骤和作图语言，理解作图的依据．3.能够运用尺规作图的方法作轴对称图形或成轴对称图形的对称轴，解决简单的作图选址问题．（难点）
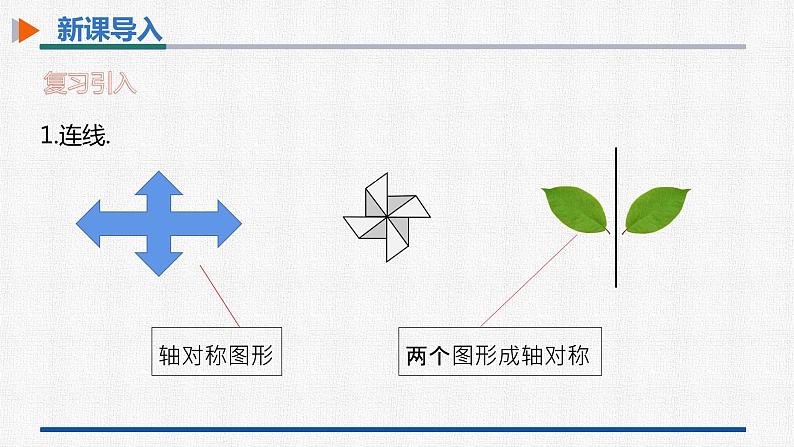
2.两个图形成轴对称的性质是什么？
如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线.
3.轴对称图形的性质是什么？
轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线.
4.线段垂直平分线的性质是什么？
线段垂直平分线上的点与这条线段两个端点的距离相等.
5.线段垂直平分线的判定定理是什么？
与线段两个端点距离相等的点在这条线段的垂直平分线.
探究 （1）观察图①的两个平面图形，它们是轴对称的吗？该如何验证你的判断呢?
（2）不折叠图形，你能准确地作出图②（轴对称图形）的对称轴吗？
图① 图②
如果两个图形成轴对称，其对称轴就是任何一对对应点所连线段的垂直平分线.因此，我们只要找到一对对应点，作出连接它们的线段的垂直平分线，就可以得到这两个图形的对称轴.
例 如图，点A和点B关于某条直线成轴对称，你能作出这条直线吗？
分析：我们只要连接点A和点B,作出线段AB的垂直平分线，就可得到点A和点B的对称轴.为此作出到点A,B的距离相等的两点，即线段AB的垂直平分线上的两点，从而作出线段AB的垂直平分线.
CD就是所求作的直线.
分析：轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线.所以只要找到任意一组对应点，作出对应点所连线段的垂直平分线，就得到此图形的对称轴.
做法：（1）找出五角星的一对对应点A和A′，连接AA′；（2）作出线段AA′的垂直平分线l，则l就是这个五角星的一条对称轴.
作法：（1）找出五角星的一对对应点A和A′，连接AA′；
（2）作出线段AA′的垂直平分线l，则l就是这个五角星的一条对称轴.
如图，作出成轴对称的△ABC和△A′BC′的对称轴l.
作法：（1）A和A′是对称点，连接AA′.
（2）作出线段AA′的垂直平分线，则该垂直平分线就是所求作的对称轴l.
作轴对称图形或成轴对称的两个图形的对称轴
（1）作对称轴的依据：如果一个图形是轴对称图形或两个图形成轴对称，其对称轴就是任何一对对应点所连线段的垂直平分线.（2）作对称轴的步骤：①找：找到轴对称图形或成轴对称的两个图形的任意一对对应点（一般找图形的顶点或转折点，这样做出的图形更准确）；②连：连接这对对应点；③作：做出对应点所连线段的垂直平分线，该垂直平分线就是对称轴.
③作这对对应点所连线段的垂直平分线，该垂直平分线就是对称轴
1.( 2021•贵阳)如图,已知线段AB=6 ,利用尺规作AB的垂直平分线,步骤如下:①分别以点A , B为圆心,以b的长为半径作弧,两弧相交于点C和D .②作直线CD .直线CD就是线段AB的垂直平分线.则b的长可能是（ ）A.1 B.2 C.3 D.4
5. ( 2021•东莞市模拟)尺规作图要求:a.过直线外一点作这条直线的垂线;b.作线段的垂直平分线;c.过直线上一点作这条直线的垂线;d.作角的平分线.其中与a、b、c、d四个作图要求依次对应的图形是　　 ．(填序号)
6.作出下列图形的对称轴.
解：直线l1为图①的对称轴.直线l2为图②的对称轴.
图① 图②
7.如图，已知∠AOB和C，D两点，求作一点P，使PC=PD，并且使点P到∠AOE两边的距离相等.
解：如图.（1）作线段CD的垂直平分线；
（2）作∠AOB的平分线；
（3）垂直平分线与角平分线的交点即为所求作的点P.