人教版14.1.4 整式的乘法课文内容ppt课件

这是一份人教版14.1.4 整式的乘法课文内容ppt课件，共26页。PPT课件主要包含了学习目标，新课导入，单项式与单项式相乘，复习引入，系数相乘，同底数幂相乘，切记不要漏乘，单项式乘单项式示例，练一练，40a5b2等内容，欢迎下载使用。
1.了解并掌握单项式与多项式相乘的运算法则，能够灵活地进行单项式与多项式相乘的运算.（重点）2.掌握单项式与多项式相乘运算法则的推导.（难点）
（2）它的运算法则是什么？
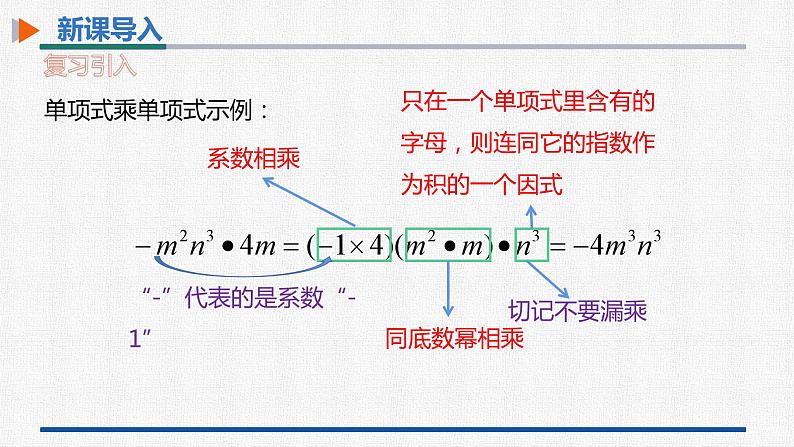
单项式与单项式相乘，把它们的系数、同底数幂分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式.
只在一个单项式里含有的字母，则连同它的指数作为积的一个因式
“-”代表的是系数“-1”
填空：(1) 2x4•x3= ; （-5a4）•（-8ab2）= ; (2) （-2a）3（-3a）2= ； •2a3b=-2a3b2．(3) 已知长方体的长是4×104厘米，宽是1.5×103厘米，高是2×103厘米，那么它的体积是 立方米．
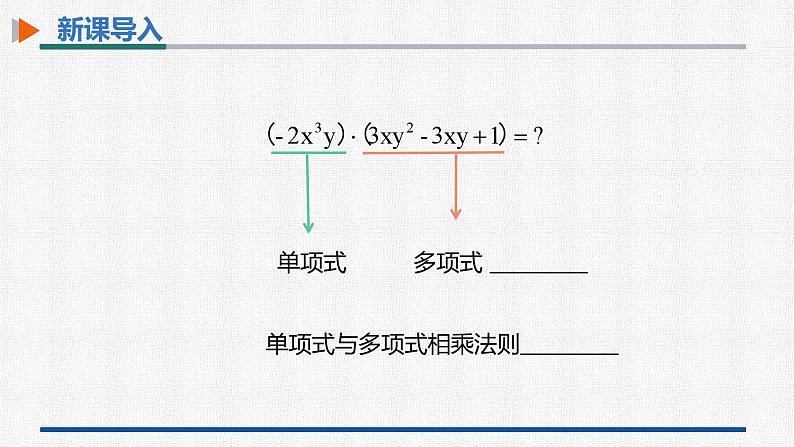
多项式
单项式
单项式与多项式相乘法则
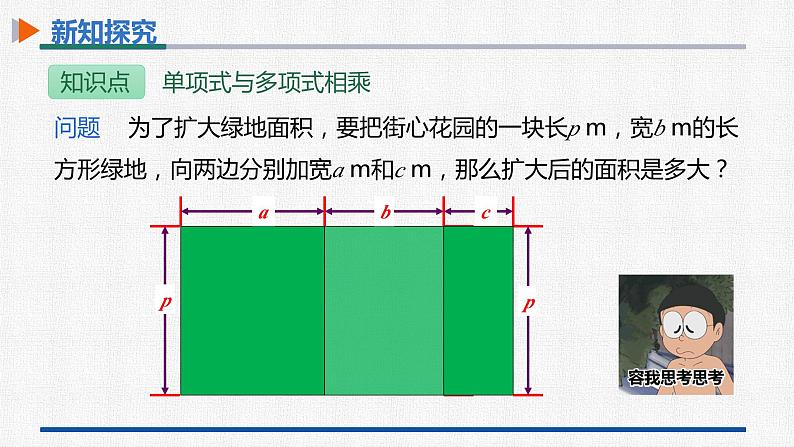
问题 为了扩大绿地面积，要把街心花园的一块长p m，宽b m的长方形绿地，向两边分别加宽a m和c m，那么扩大后的面积是多大？
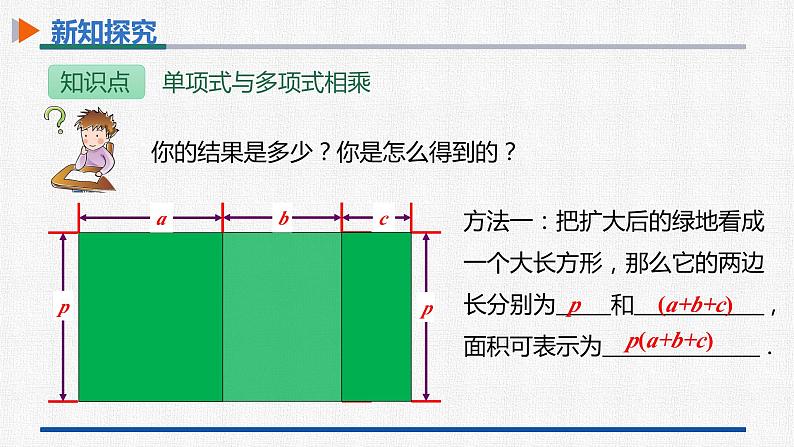
方法一：把扩大后的绿地看成一个大长方形，那么它的两边长分别为 和 ,面积可表示为 .
方法二：把扩大后的绿地看成三个小长方形，它们的面积可分别表示为 、 、 ，那么扩大后的绿地面积可表示为 .
不管用哪种方法得到的面积，两者表示的都是同一个量，所以
我们可以根据乘法分配率得到这个等式.
符号表示：p(a+b+c)=pa+pb+pc（p，a，b，c都是单项式）.
单项式与多项式相乘的步骤
(1)单项式分别乘以多项式的每一项，即转化成单项式乘单项式;
(2) 将单项式与单项式相乘的结果相加.
例 计算：(1)(-4x2)•(3x+1)；
结果的项数与多项式的项数相同.
解：(-4x2)•(3x+1)
=(-4x2)(3x)+(-4x2)×1
=(-4×3）(x2•x)+(-4x2)
=-12x3-4x2;
多项式中的“1”项不要漏乘.
多项式中的每一项都包括它前面的符号，“-”不要忘记.
计算：x2（x-1）+2x（x2-2x+3）．
解：原式=x2•x+x2×（-1）+2x•x2+2x•（-2x）+2x×3
=x3-x2+2x3-4x2+6x
=3x3-5x2+6x．
混合运算中，有同类项的必须合并，从而得到最简结果.
多项式中的“-1”项不要漏乘.
运用单项式与多项式相乘的法则进行计算时，应注意：(1)符号问题，多项式中的每一项都包括它前面的符号，积的符号由单项式的符号与多项式中每一项的符号共同决定；(2) 单项式与多项式相乘，结果是一个多项式，其项数与因式中多项式的项数相同；(3)不要出现漏乘现象，尤其是多项式中的“1”和“-1”项;(3)对于混合运算，应注意运算顺序，先算乘方，有同类项的必须合并，从而得到最简结果.
一般地，单项式与多项式相乘，就是用单项式去乘多项式的每一项，再把所得的积相加.
①单项式与多项式中的每一项相乘
1.下列运算正确的是（　　）A．2a（a-1）=2a2-aB．a（a+3b）=a2+3abC．-3（a+b）=-3a+3bD．a（-a+2b）=-a2-2ab
【解析】A.2a（a-1）=2a2-2a，故本选项不合题意；B．a（a+3b）=a2+3ab，故本选项符合题意；C．-3（a+b）=-3a-3b，故本选项不合题意；D．a（-a+2b）=-a2+2ab，故本选项不合题意．故选B．
2.今天数学课上，老师讲了单项式乘以多项式，放学回到家，小明拿出课堂笔记复习，发现一道题：-3xy（4y-2x-1）=-12xy2+6x2y+□，□的地方被钢笔水弄污了，你认为□内应填写（　　）A．3xy B．-3xy C．-1 D．1
4.如果2xy2•A=6x2y2-4x3y3，那么A= ．
3.一个长方体的长、宽、高分别是（3x-4）米，2x米和x米，则这个长方体的体积是 立方米．
【解析】由题意可得，这个长方体的体积是（3x-4）•2x•x=（3x-4）•2x2=（6x3-8x2）立方米．故答案为（6x3-8x2）立方米．
5.已知x2-4x-1=0，则代数式x（x-4）+1的值为　 　.
【解析】∵x2-4x-1=0，∴x2-4x=1.∴x（x-4）+1=x2-4x+1=1+1=2.
6.计算：(1)4(a-b+1)=___________________；
(3)(2x-5y+6z)(-3x) =___________________；
-6x2+15xy-18xz
(2)（2021江西模拟）ab2（-2a+b）= ．
（1）2（2x2-xy）+x（x-y）； （2）ab（2ab2-a2b）-（2ab）2b+a3b2．
（2）原式=ab•2ab2+ab•（-a2b）-4a2b2•b+a3b2=2a2b3-a3b2-4a2b3+a3b2=-2a2b3．
解：（1）原式=2•2x2+2•（-xy）+x•x+x•（-y）=4x2-2xy+x2-xy=5x2-3xy．
8.已知-x3（x2+ax+1）+2x4中不含有x的四次项，求a的值.
解：原式=-x5-ax4-x3+2x4=-x5+（2-a）x4-x3.
∵-x3（x2+ax+1）+2x4中不含有x的四次项，
【分析】利用多项式乘以单项式法则及合并同类项法则进行化简；不含x的四次项，则x的四次项的系数为0，由此确定a的值．
解得a=2．故a的值为2.