2022-2023学年江苏省南京市联合体八年级（上）期中数学试卷

这是一份2022-2023学年江苏省南京市联合体八年级（上）期中数学试卷，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年江苏省南京市联合体八年级（上）期中数学试卷
一、选择题（本大题共8小题，每小题2分，共16分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）
1．下列“表情”中属于轴对称图形的是　　
A． B． C． D．
2．如图，，若，，则的度数为　　

A． B． C． D．
3．下列条件中能构成直角三角形的是　　
A．2、3、4 B．3、4、5 C．4、5、6 D．5、6、7
4．如图，用直尺和圆规作一个角的平分线，是运用了“全等三角形的对应角相等”这一性质，由作图所得条件，判定三角形全等运用的方法是　　

A． B． C． D．
5．下列说法中，正确的是　　
A．周长相等的两个直角三角形全等
B．周长相等的两个钝角三角形全等
C．周长相等的两个等腰三角形全等
D．周长相等的两个等边三角形全等
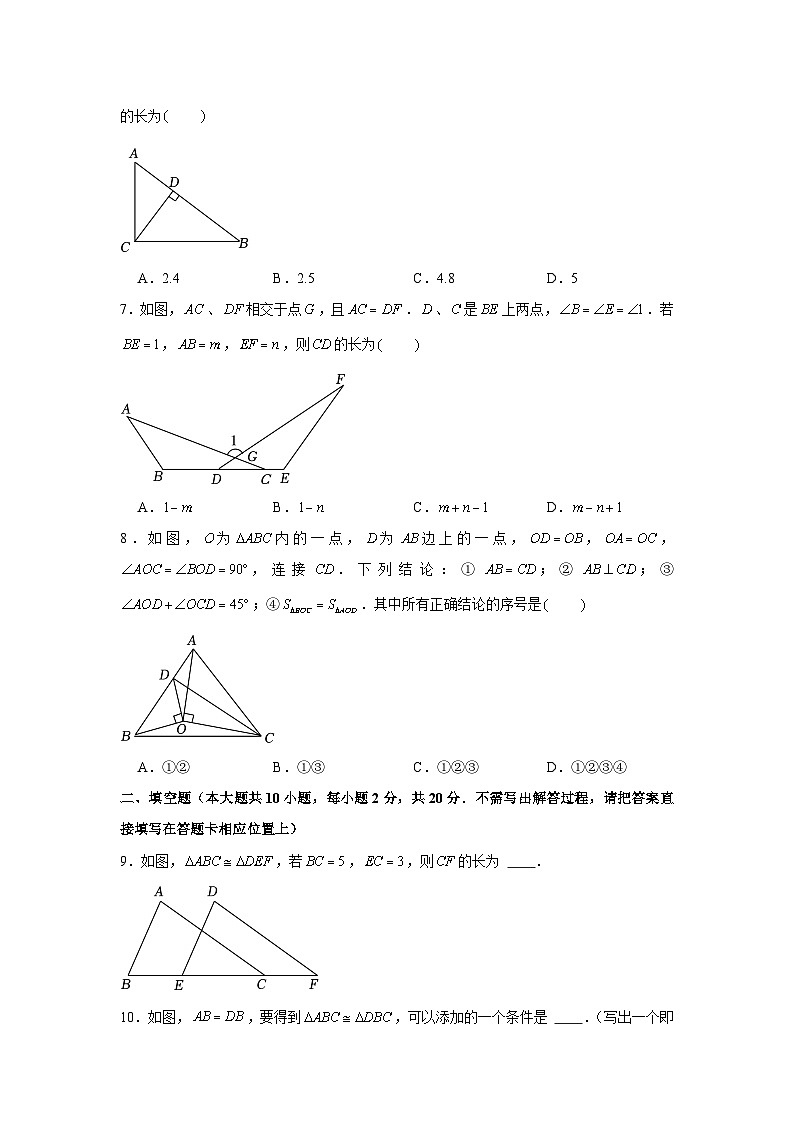
6．如图，在中，，，垂足为．若，，则的长为　　

A．2.4 B．2.5 C．4.8 D．5
7．如图，、相交于点，且．、是上两点，．若，，，则的长为　　

A． B． C． D．
8．如图，为内的一点，为边上的一点，，，，连接．下列结论：①；②；③；④．其中所有正确结论的序号是　　

A．①② B．①③ C．①②③ D．①②③④
二、填空题（本大题共10小题，每小题2分，共20分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）
9．如图，，若，，则的长为 　　．

10．如图，，要得到，可以添加的一个条件是 　　．（写出一个即可）

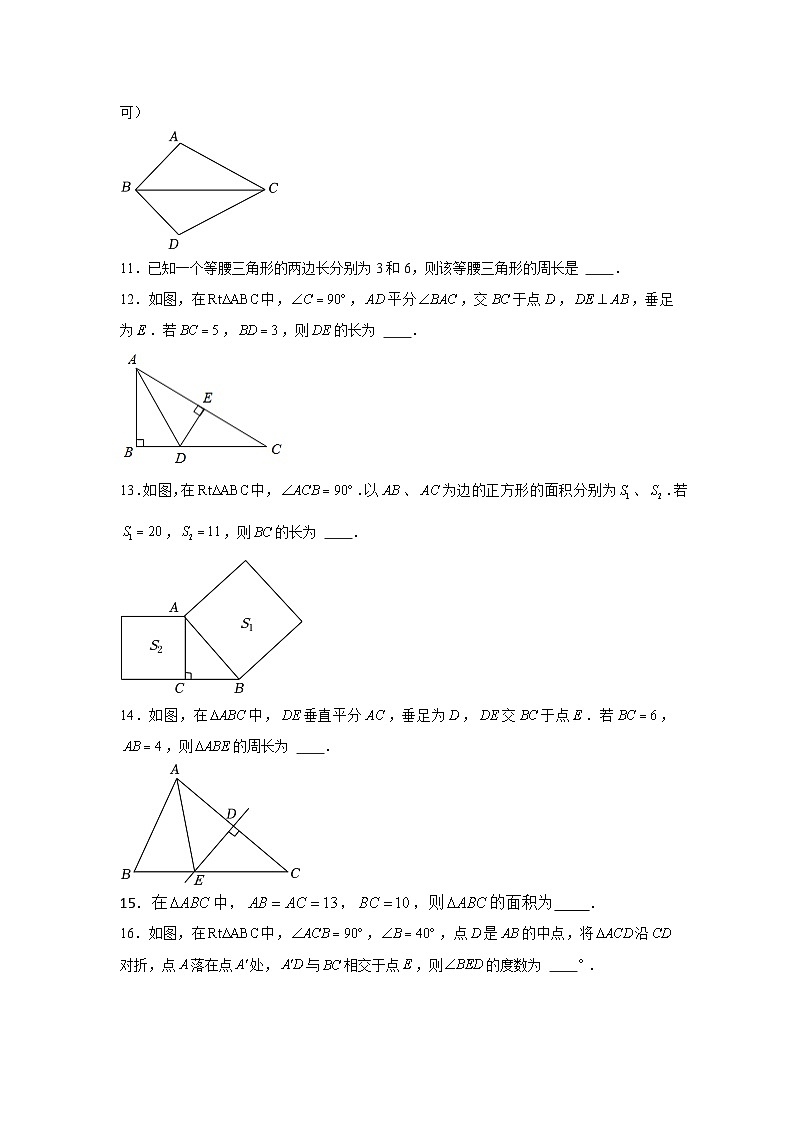
11．已知一个等腰三角形的两边长分别为3和6，则该等腰三角形的周长是 　　．
12．如图，在中，，平分，交于点，，垂足为．若，，则的长为 　　．

13．如图，在中，．以、为边的正方形的面积分别为、．若，，则的长为 　　．

14．如图，在中，垂直平分，垂足为，交于点．若，，则的周长为 　　．

15．在中，，，则的面积为　 　．
16．如图，在中，，，点是的中点，将沿对折，点落在点处，与相交于点，则的度数为 　　．

17．如图，在中，，的垂直平分线交于点，交的延长线于点．若，，则的长为 　　．

18．如图，平分，．若，，则的长为 　　．

三、解答题（本大题共8小题，共64分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
19．（6分）如图，与交于点，，．
求证：．

20．（8分）如图，在四边形中，，，，，．求证：．

21．（8分）证明：等腰三角形的两底角相等（简称“等边对等角” ．
已知：如图，在中，　　．
求证：　　．
证明：

22．（8分）如图，在中，，．点在直线上，分别过点、作直线于点，直线于点．
（1）求证：；
（2）设三边分别为、、，利用此图证明勾股定理．

23．（8分）如图，在四边形中，，，是上一点．
（1）求证：；
（2）若是的中点，延长交于点，且，求的度数．

24．（8分）如图，在等边三角形中，，、相交于点．
（1）求证：；
（2）过点作，垂足为．若，，则的长为 　　．

25．（8分）已知图①、图②都是轴对称图形．仅用无刻度直尺，按要求完成下列作图（保留作图痕迹，不写作法）
（1）在图①中，作出该图形的对称轴；
（2）在图②中，作出点的对称点．

26．（10分）【旧题重现】
（1）《学习与评价》有这样一道习题：
如图①，、分别是和△的、边上的中线，，，．
求证：△．
证明的途径可以用下面的框图（图②表示，请填写其中的空格．
【深入研究】
（2）如图③，、分别是和△的、边上的中线，，，．判断与△是否仍然全等，并说明理由
【类比思考】
（3）下列命题中是真命题的是 　　（填写相应的序号）
①两角和第三个角的角平分线分别相等的两个三角形全等；
②一边和这条边上的中线以及高分别相等的两个三角形全等；
③斜边和斜边上的高分别相等的两个直角三角形全等；
④两边和第三边上的高分别相等的两个三角形全等；
⑤底边和一腰上的中线分别相等的两个等腰三角形全等．

参考答案与解析
选择、填空题答案
1
2
3
4
5
6
7
8
D
D
B
D
D
A
C
D
9.2 10.或 11.15 12.3 13.3 14.10
15.60 16.120 17.
19.证明：在和中，
，．
20.证明：如图，连接.

，，，
，
在中，，，
，
是直角三角形，．
21.解：
证明：如图，过点作，垂足为.

，.
在和中，，，
，.
22.证明：（1），，
，
，，
.
在和中，
，，，
.
（2）由（1）知，，，，
，
又，
，
整理，得．
23.（1）证明：在和中，
，
，.
在和中，
，.
（2）设的度数为，
在中，，是的中点，
，.
，.
，.
，
．.
在中，，
，解得．
24.（1）证明：是等边三角形，
，.
在和中，，
，.
，.
（2）9
25.解：（1）如图1所示：
（2）如图2所示：

图1 图2
26.解：（1）①；②；③；④
（2）与△仍然全等，理由如下：
如图，延长至，使，连接，延长至，使，连接．

和分别是和△的和边上的中线，
，．
在和中，
，
，.
同理，．
，．
，，，．
，△．
，，
，.
又，，
△.
（3）①②③⑤