2022-2023学年江苏省南京市玄武区九年级（上）期中数学试卷

这是一份2022-2023学年江苏省南京市玄武区九年级（上）期中数学试卷，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2022-2023学年江苏省南京市玄武区九年级（上）期中数学试卷
一、选择题（本大题共6小题，每小题2分，共12分.在每小题给出的四个选项中，只有一项是符合题目要求的.）
1．已知的半径为，圆心到直线的距离为，直线与的位置关系是　　
A．相离 B．相切 C．相交 D．无法确定
2．若关于的一元二次方程有两个相等的实数根，则实数的值为　　
A． B． C． D．4
3．用“配方法”解一元二次方程，下列变形正确的是　　
A． B． C． D．
4．如图，是直径，点，在半圆上，若，则　　

A． B． C． D．
5．如图，在一块正三角形飞镖游戏板上画一个正六边形（图中阴影部分），假设飞镖投中游戏板上的每一点是等可能的（若投中边界或没有投中游戏板，则重投1次），任意投掷飞镖1次，则飞镖投中阴影部分的概率为　　

A． B． C． D．
6．如图，在中，是直径，点，，在圆上，，，，．下列结论：①；②；③；④，其中正确结论的个数是　　

A．4个 B．3个 C．2个 D．1个
二、填空题（本大题共10小题，每小题2分，共20分.不需写出解答过程中，请把答案直接填写在答题卡相应位置上）
7．一元二次方程的解是：　　．
8．超市决定招聘广告策划人员一名，某应聘者三项素质测试的成绩如表：
测试项目
创新能力
综合知识
语言表达
测试成绩（分数）
70
80
90
将创新能力、综合知识和语言表达三项测试成绩按的比例计入总成绩，则该应聘者的
总成绩是　 　分．
9．已知，是一元二次方程的两根，则　　．
10．一只不透明的袋子中共有2个白球和若干个红球，这些球除颜色外其他都相同．从袋中随机摸出1个球，恰好是红球的概率为，则袋中红球的个数是 　　个．
11．某地区新能源汽车保有量2020年底达到30万辆，2022年底达到41万辆．设该地区这两年新能源汽车保有量的年平均增长率为，根据题意可列方程为 　　．
12．如图，在的内接四边形中，，．若点在上，则
　 　．

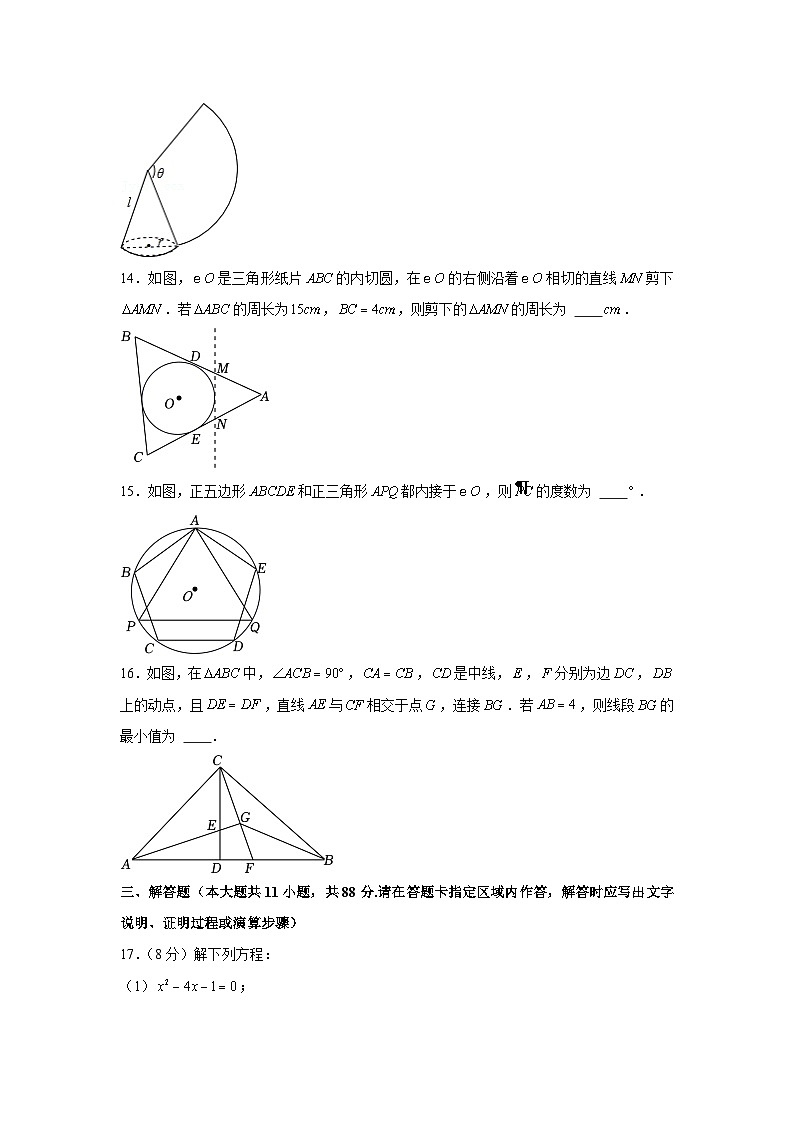
13．如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形，若圆锥母线，扇形的圆心角，则该圆锥的底面圆的半径长为 　　．

14．如图，是三角形纸片的内切圆，在的右侧沿着相切的直线剪下．若的周长为，，则剪下的的周长为 　　．

15．如图，正五边形和正三角形都内接于，则的度数为 　　．

16．如图，在中，，，是中线，，分别为边，上的动点，且，直线与相交于点，连接．若，则线段的最小值为 　　．

三、解答题（本大题共11小题，共88分.请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
17．（8分）解下列方程：
（1）；
（2）．
18．（8分）甲、乙两名运动员在相同条件下6次射击成绩的折线统计图如下：
（1）填表（单位：环）

平均数
中位数
众数
甲的射击成绩
①　　
8
③　　
乙的射击成绩
8
②　　
9
（2）计算甲、乙射击成绩的方差，并判断哪位运动员的射击成绩更稳定？

19．（7分）计划选派护士支援某地的防疫工作，决定用随机抽取的方式从4名护士中确定人选，其中1人是团员，其余3人均是党员．
（1）随机抽取1人，恰好是党员的概率为 　　；
（2）随机抽取2人，求被抽到的两名护士恰好都是党员的概率．
20．（8分）如图，弓形是由和弦所围成的图形，弓形的高是的中点到的距离，点是所在圆的圆心，，弓形的高为．
（1）求的半径；
（2）经测量的度数约为，则弓形的面积为 　　．

21．（8分）已知关于的方程为常数）．
（1）求证：不论取何值，该方程总有两个不相等的实数根；
（2）若该方程的两个实数根为和，且，求的值．
22．（8分）如图，在中，，以为直径的与，分别交于点，，连接．
（1）求证：；
（2）延长，相交于点，若，则的度数为 　　．

23．（7分）某水果成本价为12元千克．经调研，该水果在某平台上的售价为28元千克时，可销售300千克；售价每降2元，销量将增加100千克．为了推广宣传，商家决定降价促销，同时尽量减少库存，若销售该水果获利6000元，则售价应降低多少元？
24．（6分）已知直线与相切于点．用直尺和圆规完成下列作图．（保留作图痕迹，不写作法）
（1）在图①中，作出直线，使与相切，且；
（2）在图②中，作出一条直线，使与相切，且与的夹角中有一个角为．

25．（9分）如图，在中，是的直径，是的切线，切点是，连接，过点作，与交于点，连接．
（1）求证：是的切线；
（2）若的半径为3，，求的长度．

26．（9分）如图，在一块长，宽的矩形绿地内，建一个矩形花圃．
（1）要使矩形花圃的面积是矩形绿地面积的一半，且矩形花圃四周的绿地等宽，求矩形花圃的周长；
（2）要使矩形花圃的面积是矩形绿地面积的一半，且矩形花圃的周长是矩形绿地周长的一半，问这样的矩形花圃能否围出？如果能，请求出矩形花圃的长和宽；如果不能，请说明理由．

27．（10分）已知，是的两条弦，且．
（1）如图1，是的直径．求证：；
（2）如图2，连接．请用无刻度的直尺作出的一条弦，使．（保留作图痕迹，不写作法）
（3）如图3，四边形是的内接四边形，．若的半径为6，，且，则的长度为 　　．

图1 图2 图3
参考答案与解析
选择、填空题答案
1
2
3
4
5
6
A
B
D
C
D
B
7.， 8.77 9.2 10.4 11. 12.125 13.2 14.7 15.24 16.
17.解：（1），
，
，
，
，
∴，.
（2），
，
，
，
或，
∴，．
18.解：①8；②8.5；③8
（2）甲射击环数的方差，
乙射击环数的方差，
，乙运动员射击成绩更稳定．
19.解：（1）
（2）如图所示：

共有12种可能，所以两名护士都是党员的概率为．
20.解：（1）如图，过点作于，交于，
则，，
设的半径为，则，.
在中，由勾股定理，得，解得.

（2）
21.（1）证明：，
不论取何值，该方程总有两个不相等的实数根.
（2）解：根据根与系数的关系，得，，
，，解得.
22.（1）证明：四边形是的内接四边形，.
，，
，.
（2）42
23.解：设售价应降低元，则每天可售出（千克），
依题意，得，解得，，
要尽量减少库存，．
答：售价应降低6元．
24.解：（1）如图1中，直线即所求.
（2）如图2，直线即所求．

图1 图2
25.（1）证明：如图1，连接，
是的切线，.
，，.
，，.
在和中，
，.
是的半径，是的切线.

（2）解：如图2，连接.
在中，，
是的直径，，.
，，
，即，解得．

26.解：（1）设矩形花圃四周绿地的宽为，则矩形花圃的长为，宽为，
依题意，得，
整理，得，解得，（不符合题意，舍去），
．
答：矩形花圃的周长为．
（2）不能围成符合题意的矩形，理由如下：
设矩形花圃的长为，则宽为，
依题意，得，整理，得．
，所列方程没有实数根，
不能围成符合题意的矩形花圃．
27.（1）证明：如图1，连接，

图1
是的直径，，.
，，.
（2）解：如图2，连接并延长交于点，连接，则.

图2
（3）解：