2022-2023学年江苏省苏州市九年级（上）期末数学试卷

这是一份2022-2023学年江苏省苏州市九年级（上）期末数学试卷，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2022-2023学年江苏省苏州市九年级（上）期末数学试卷
一、选择题（本大题共8小题，每小题3分，共24分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将答案填涂在答题卡相应位置上）
1．有一组数据：11，11，12，15，16，则这组数据的中位数是　　
A．11 B．12 C．15 D．16
2．方程的根是　　
A． B．2 C．或 D．2或
3．若的半径为，点到圆心的距离为，那么点与的位置关系是　　
A．点在圆内 B．点在圆上 C．点在圆外 D．不能确定
4．若抛物线的对称轴是轴，则的值是　　
A． B． C．0 D．2
5．如图，点，，在上，若，则的度数为　　

A． B． C． D．
6．我们可用“斜尺”测量管道的内径（如图），若玻璃管的内径正对“30”刻度线，已知长为，，则玻璃管内径的长度等于　　

A． B． C． D．
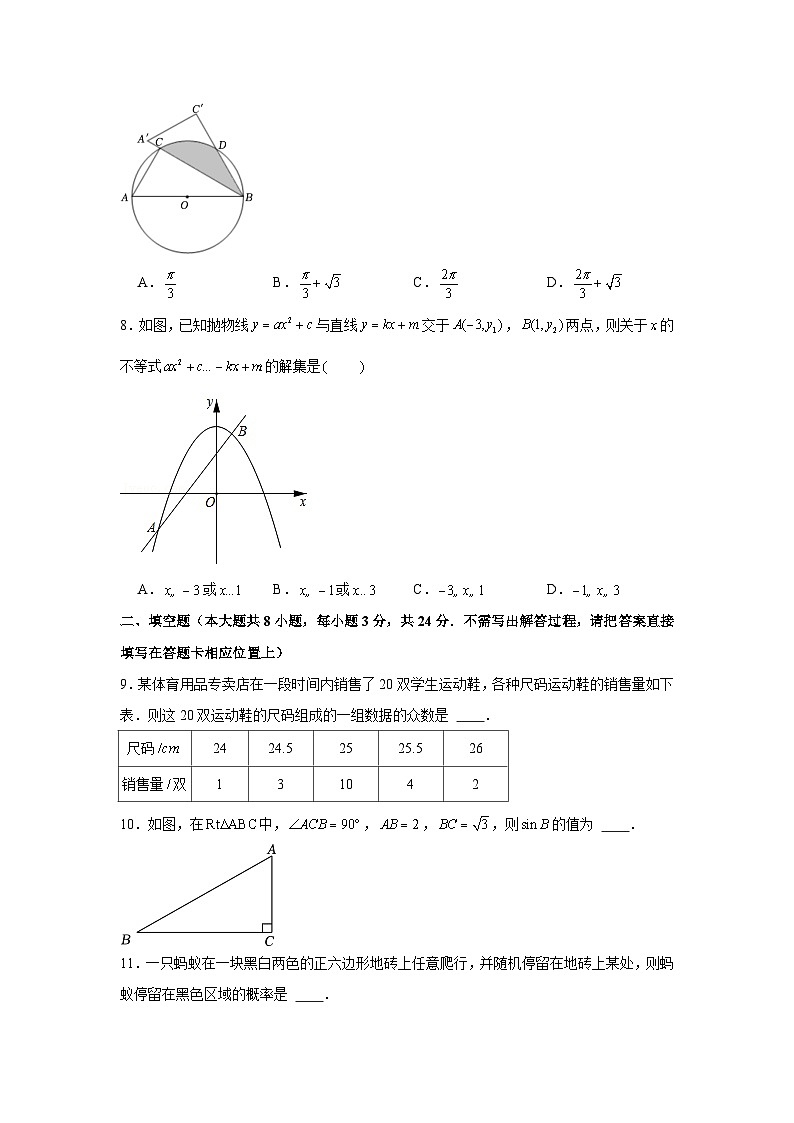
7．如图，为上一点，是的直径，，，现将绕点按顺时针方向旋转后得到△，交于点，则图中阴影部分的面积为　　

A． B． C． D．
8．如图，已知抛物线与直线交于，两点，则关于的不等式的解集是　　

A．或 B．或 C． D．
二、填空题（本大题共8小题，每小题3分，共24分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）
9．某体育用品专卖店在一段时间内销售了20双学生运动鞋，各种尺码运动鞋的销售量如下表．则这20双运动鞋的尺码组成的一组数据的众数是 　　．
尺码
24
24.5
25
25.5
26
销售量双
1
3
10
4
2
10．如图，在中，，，，则的值为 　　．

11．一只蚂蚁在一块黑白两色的正六边形地砖上任意爬行，并随机停留在地砖上某处，则蚂蚁停留在黑色区域的概率是 　　．

12．若、是一元二次方程的两个实根，则值是　　．
13．如图，与相切于点，是的弦，且，，则的半径长为 　　．

14．如图，在四边形中，点在上，，，若面积为5，的面积为1，则的面积是　　．

15．在中，，，则度数的最大值为 　　．
16．已知抛物线过，两点．若，则下列四个结论中正确的是 　　．（请将所有正确结论的序号都填写到横线上）：①；②；③点，，，在抛物线上，若，，则；④关于的一元二次方程必有两个不相等的实数根．
三、解答题（本大题共11小题，共82分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
17．（5分）计算：．
18．（5分）解方程：．
19．（6分）为落实“双减”政策，某中学在课后服务时间开设了四个兴趣小组，分别为：机器人，：交响乐，：油画，：古典舞．为了解学生的报名情况（每名学生只报一个兴趣小组），现随机抽取部分学生进行调查，并根据调查结果绘制了如下两幅不完整的统计图．

请根据图文信息回答下列问题：
（1）此次调查共抽取 　　名学生；
（2）请将条形统计图补充完整；
（3）扇形统计图中，项目所对应的扇形圆心角的度数为 　　．
20．（8分）为深入学习贯彻党的二十大精神，我市某中学决定举办“青春心向党，奋进新征程”主题演讲比赛，该校九年级有二男二女共4名学生报名参加演讲比赛．
（1）若从报名的4名学生中随机选1名，则所选的这名学生是女生的概率是 　　；
（2）若从报名的4名学生中随机选2名，用树状图或表格列出所有可能的情况，并求出这2名学生都是男生的概率．
21．（8分）如图，测绘飞机在同一高度沿直线由向飞行，且飞行路线经过观测目标的正上方．在第一观测点处测得目标的俯角为，航行1000米后在第二观测点处测得目标的俯角为，求第二观测点与目标之间的距离．

22．（8分）把一根长8米的绳子剪成两段，并把每一段绳子围成一个正方形．
（1）要使这两个正方形面积的和等于2平方米，应该怎么剪？
（2）这两个正方形面积的和可能等于平方米吗？请说明理由．
23．（8分）在半径为的圆形纸片中，剪出一个圆心角为的扇形（图中的阴影部分）．
（1）求这个扇形的半径；
（2）若用剪得的扇形纸片围成一个圆锥的侧面，求所围成圆锥的底面圆半径．

24．（8分）已知二次函数的图像与轴有唯一公共点．
（1）求的值；
（2）当时，函数的最大值为4，且最小值为0，则实数的取值范围是 　　．
25．（8分）如图，矩形中，，，点从点出发，以每秒1个单位长度的速度在射线上向右运动，运动时间为秒，连接交于点．
（1）求证：；
（2）若是以为腰的等腰三角形，求运动时间的值．

26．（9分）如图，以为直径的经过的顶点，，分别平分和，的延长线交于点，交于点，连接．
（1）求证：；
（2）求证：；
（3）若，，求的长．

27．（9分）在平面直角坐标系中，为坐标原点，直线与轴交于点，与轴交于点．二次函数的图像过，两点，且与轴交于另一点，点为线段上的一个动点（不与端点，重合）．

（1）求二次函数的表达式；
（2）如图①，过点作轴的平行线交于点，交二次函数的图像于点，记的面积为，的面积为，当时，求点的坐标；
（3）如图②，连接，过点作的垂线，过点作的垂线，与交于点，试探究的值是否为定值？若是，请求出的值；若不是，请说明理由．


参考答案与解析
选择、填空题答案
1
2
3
4
5
6
7
8
B
D
A
C
B
B
C
D
9.25 10. 11. 12. 13.1 14. 15.45 16.②③④
17.解：


．
18.解：，
则或，
或．
19.解：（1）100
（2）的人数为，
条形统计图如图所示：

（3）144
20.解：（1）
（2）画树状图如下：

由图可得共有12种情况，是男生的情况有2种，
名学生都是男生的概率，
这2名学生都是男生的概率为．
21.解：如图，过作，垂足为，

，，，
米，（米，
，，
，
在中，，
（米.
答：第二观测点与目标之间的距离为米．
22.解：（1）设剪成的一段为米，则另一段就为米，
由题意得，解得．
答：剪成的一段为4米，则另一段就为4米；
（2）设剪成的一段为米，则另一段就为米，
由题意，得，
整理，得，
解得，舍去，，舍去，
所以这两个正方形面积的和不可能等于．
23.解：（1）如图，连接，，，过点作，垂足为，

，，，
，，是等边三角形，
，，
这个扇形的半径为3．
（2）设圆锥底面圆的半径为，
根据题意，得，解得．
故圆锥底面圆的半径为．
24.解：（1）二次函数的图像与轴有唯一公共点，
一元二次方程的判别式等于0，
，，解得.
（2）
25.（1）证明：四边形是矩形，
，.
又，.
（2）解：四边形是矩形，，，.
由题意，知，.
①当时，即，
，
，∴，解得；
②当时，，
，
，∴，整理，得，
两边同时平方，得，整理，得，
解得或（舍去）．
综上，是以为腰的等腰三角形时，或．
26.（1）证明：平分，.
，.
（2）证明：为的直径，．
，分别平分和，
，．
，．
，，
，.
（3）解：如图，连接，交于点．

，
，，．
，，
由（2）得为等腰直角三角形，，
，解得，
在中，，
在中，，
，解得，
，．
27.解：（1）在一次函数中，当时，，当时，，
，，
将，代入抛物线得解得
.
（2）如图①，连接，设点坐标为，
轴，点的坐标为，点的坐标为.
由题意，得
，，
，，
解得，（不符合题意舍去），
的坐标为.

（3）如图②，过作轴.
，，轴，，
，，，，
，，
，.
，，，.
，.
设点坐标为，点坐标为，
可得，解得，
，
，．